【基本】たすき掛けを使った因数分解

【基本】因数分解では、いくつかの簡単なケースでの因数分解を紹介しました。ここでは、「たすき掛け」という方法を使った因数分解を見ていきます。

因数分解の公式

因数分解は、展開の逆の操作です。なので、展開の公式が、そのまま因数分解の公式にもなります。

しかし、【基本】展開の公式で挙げた公式が、【基本】因数分解ですべて出てきたわけではありません。1つだけ少し難しいものがあったんですね。それが次の公式です。

左辺から右辺を導くのは、【基本】因数分解で出てきた他の公式よりも難しいです。具体例を見ていきながら、この形の因数分解の仕方を見ていきます。

例題1

$acx^2 +(ad+bc)x +bd = (ax+b)(cx+d)$ と見比べながら考えてみます。因数分解をするには、$a,b,c,d$ という4つの数字を見つけなくてはいけません。

求めるものが多いので、どこから手をつけたらいいかわかりにくいですね。こういう場合は、制限が厳しいところから考えていくのがいいです。そのことを踏まえてみていきましょう。

$x^2$ の係数は「掛けて2」となるものなので、$(1,2)$ の組み合わせしかありません。本当は負の組合せもありますが、今回はすべての係数が正なので考えなくてもかまいません。

$x$ の係数は $ad+bc$ なので、制限が緩く、組合せはたくさん考えられます。なので、これは後回しにします。次に、定数項（数字だけの部分）を見ると「掛けて3」なので、$(1,3)$ の組み合わせしかありません。

つまり、係数が全部整数なら、$(a,c)$ は $(1,2)$、$(2,1)$ のどちらかで、$(b,d)$ は $(1,3)$、$(3,1)$ のどちらかであることがわかります。これらを組み合わせて、後回しにしていた $x$ の係数について考えます。

もし、$(a,c)=(1,2)$ で、$(b,d)=(1,3)$ なら、$(x+1)(2x+3)$ となります。これを展開すると $x$ の係数は5であることが分かります。なので、違いますね。

一方、$(b,d)=(3,1)$ なら、$(x+3)(2x+1)$ なので、展開すると $x$ の係数は7であることが分かります。なので、これが正解であることが分かります。

ちなみに、$(a,c)=(2,1)$ のときは、掛け算の順番が入れ替わるだけなので、考えなくてもかまいません。$(2x+1)(x+3)$ となるだけですね。

よって、\[ 2x^2+7x+3=(x+3)(2x+1) \]となることがわかります。

このように、少し面倒ですが、考えられるパターンを順番に試して、係数を見つけなければいけません。

たすき掛け

上の問題では、$(x+1)(2x+3)$ や $(x+3)(2x+1)$ といった式を作って展開して計算していましたが、もう少し簡単に考えたいですよね。そこでよく使われるのが「たすき掛け」という方法です。やっていること自体は同じなのですが、いちいち式を書かなくていい分、楽になります。

$acx^2 +(ad+bc)x +bd = (ax+b)(cx+d)$ と見比べながら、$2x^2+7x+3$ を考えてみます。まず、$ac=2$なので、$(a,c)=(1,2)$ の組合せが考えられます。このとき、次のように数字を縦に書きます。

（たすき掛け第1段階）
1
2

次に、定数項を見ると $bd=3$ なので、$(b,d)=(1,3)$ の組合せが考えられます。他にもありますが、まずはこの組み合わせから考えます。それぞれ、横に数字を書きます。

（たすき掛け第2段階）
1　1
2　3

次にするのは、$x$ の係数のチェックですね。$ad+bc$ を計算するするために、上の状態で、左上と右下、右上と左下を掛けて、足します。これが、たすき掛け第3段階です。このように"クロス"して掛けるので、「たすき掛け」と読んでいます。

右下の答えが、元の $x$ の係数と一致していればいいのですが、今回は違いますね。

別の組合せでも同様にしてみます。$(b,d)=(3,1)$ の組合せで考えてみます。

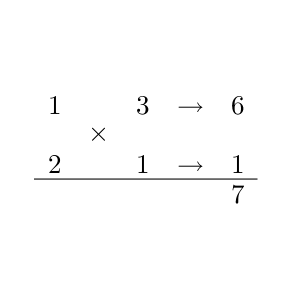
これだと右下の答えが一致しますね。このとき、上同士の数字を使った $x+3$ と、下同士の数字を使った $2x+1$ を用いて、 $(x+3)(2x+1)$ とすると、答えになります。

文字を使ってみると、右下に出てくる答えは何かが分かりやすいと思います。

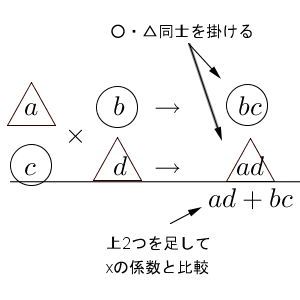
右下は $ad+bc$ となります。つまり、たすき掛けというのは、展開したときの $x$ の係数を計算しているだけなんですね。

例題2

掛け算の組合せが多くなると、もちろん、試行錯誤の回数も増えます。

$x^2$ の係数は6なので、 $(a,c)$ は $(1,6)$ や $(2,3)$ などいくつかの組合せがあります。また、定数項は -6なので、$(b,d)$ は $(-3,2)$ や $(6,-1)$ など、符号も含めていくつかの組合せがあります。

1つ1つの組合せを試していき、$x$ の係数が合うまで繰り返します。大変ですが、慣れてくればだいたい予想がつくようになってきます。数多く計算問題を繰り返せば、数字の組み合わせを見つける時間も短くなってきます。

ちなみに、試行錯誤を繰り返すと、上の式を因数分解したものは、$(3x+2)(2x-3)$ であることがわかります。

おわりに

ここでは、たすき掛けを使った因数分解を見てきました。\[ acx^2 +(ad+bc)x +bd \]の形をした式の因数分解は、$x^2$ の係数と定数項から $a,b,c,d$ の組合せを絞り、 $x$ の係数が合うようにして $(ax+b)(cx+d)$ の形に変えていきます。「$x$ の係数」を合わせるために試行錯誤する際、毎回式を書くのは大変なので、たすき掛けを使う方法を紹介しました。

「たすき掛けを使う方がわかりにくい、逆に時間がかかる」という人は、無理にたすき掛けを使わなくても大丈夫です。 $(ax+b)(cx+d)$ の形にできるのであれば、自分のやりやすい方法で $a,b,c,d$ の組合せを見つけて構いません。