【基本】補集合

🕒 2016/06/18 🔄 2023/05/01

ここでは、「東京に住んでいる人の集合」と「東京に住んで"いない"人の集合」のように、「集合 A に属していない要素の集合」を考えていきます。

📘 目次

全体集合

数学で集合を考える場合、普通は、対象となる要素をはじめに決めておきます。例えば、「自然数全体の集合」や「実数全体の集合」というように対象を決め、その中で「偶数の集合」や「0以上10以下の数の集合」などを考えていくことが普通です。このとき、もととなる一番大きい集合のことを、全体集合(universal set) と呼びます。

なぜ全体集合を考える必要があるかというと、「ある集合に属していない要素の集合」を考えるときに困るからなんですね。

例えば「東京に住んでいない人の集合」といったときに、ある人は「大阪や沖縄に住んでる人」と思うかもしれないし、別の人は「アメリカや中国に住んでいる人」と思うかもしれません。こうなると、思わぬところで話が通じなくなる可能性があります。

なので、はじめに、「ここの話では、日本に限定しますよ」とか「関東の話に限定します」とか「地球全体で考えますよ」というように、「どこを全体と考えているかを決めておく」必要があるんですね。

なお、全体集合は、普遍集合と呼ばれることもあります。

補集合

ある集合Aに対し、Aに属していない要素全体の集合を、Aの補集合(complement)と言います。

記号では $\overline{ A }$ と書きます。 $A^c$ と書く場合もあります。

例えば、全体集合が $\{1,2,3,4,5\}$ で、 $A=\{1,2,4\}$ の場合は、 $\overline{ A }=\{3,5\}$ となります。ベン図を使えば、次のようになります。

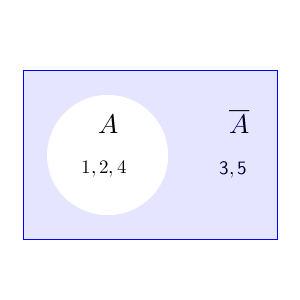
白い円の部分が集合A、それ以外の色のついた部分が $\overline{ A }$ ということです。