東京大学 理系 2023年度 第3問 解説
問題編
問題
$a$ を実数とし、座標平面上の点 $(0,a)$ を中心とする半径 $1$ の円の周を $C$ とする。
(1) $C$ が、不等式 $y\gt x^2$ の表す領域に含まれるような $a$ の範囲を求めよ。
(2) $a$ は (1) で求めた範囲にあるとする。 $C$ のうち $x\geqq 0$ かつ $y\lt a$ を満たす部分を $S$ とする。 $S$ 上の点 $\mathrm{P}$ に対し、点 $\mathrm{P}$ での $C$ の接線が放物線 $y=x^2$ によって切り取られてできる線分の長さを $L_{\mathrm{P}}$ とする。 $L_{\mathrm{Q}}=L_{\mathrm{R}}$ となる $S$ 上の相異なる2点 $\mathrm{Q,R}$ が存在するような $a$ の範囲を求めよ。
考え方
(1)は、円から攻めるか、放物線から攻めるか、複数のやり方がありえますが、解答を書きやすい方で解きましょう。
(2)は難しいことをいっているように感じるかもしれませんが、要は、 $\mathrm{P}$ を動かしたときに、 $L_{\mathrm{P}}$ が同じ値を2回とることがあるか、を考えるということです。
ただ、このイメージがつかめても、関数の形に持って行くのが一苦労。理系の場合は、どんな関数の形でも力づくで微分することができますが、できる限り簡単な式になるように頑張って変形してから微分しましょう。
解答編
問題
$a$ を実数とし、座標平面上の点 $(0,a)$ を中心とする半径 $1$ の円の周を $C$ とする。
(1) $C$ が、不等式 $y\gt x^2$ の表す領域に含まれるような $a$ の範囲を求めよ。
解答
$C$ 上の点は、実数 $\theta$ を使って、 $(\cos\theta,a+\sin\theta)$ と表すことができる。これが $y\gt x^2$ を満たすことは、すべての実数 $\theta$ に対して $a+\sin\theta \gt \cos^2\theta$ が成り立つことと同値である。
\begin{eqnarray}
a+\sin\theta & \gt & \cos^2\theta \\[5pt]
a & \gt & -\sin^2\theta -\sin\theta +1 \\[5pt]
a & \gt & -\left(\sin\theta-\frac{1}{2}\right)^2 +\frac{5}{4} \\[5pt]
\end{eqnarray}であり、右辺は $\sin\theta=\dfrac{1}{2}$ のときに、最大値 $\dfrac{5}{4}$ をとるので、 $a\gt \dfrac{5}{4}$ と同値である。
よって、求める範囲は $a\gt \dfrac{5}{4}$ …(答)
解答編 つづき
問題
(2) $a$ は (1) で求めた範囲にあるとする。 $C$ のうち $x\geqq 0$ かつ $y\lt a$ を満たす部分を $S$ とする。 $S$ 上の点 $\mathrm{P}$ に対し、点 $\mathrm{P}$ での $C$ の接線が放物線 $y=x^2$ によって切り取られてできる線分の長さを $L_{\mathrm{P}}$ とする。 $L_{\mathrm{Q}}=L_{\mathrm{R}}$ となる $S$ 上の相異なる2点 $\mathrm{Q,R}$ が存在するような $a$ の範囲を求めよ。
解答
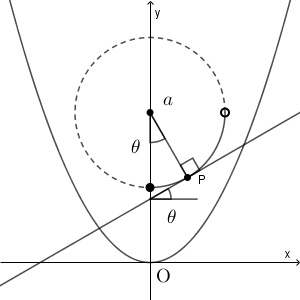
$S$ 上の点 $\mathrm{P}$ は、 $0\leqq \theta \lt \dfrac{\pi}{2}$ を使って、\[ (\sin\theta,a-\cos\theta) \]と表すことができる。
この点での $C$ の接線の傾きは $\tan\theta$ である。
よって、接線の方程式は
\begin{eqnarray}
y &=& \tan\theta(x-\sin\theta)+a-\cos\theta \\[5pt]
&=&
x\tan\theta-\frac{\sin^2\theta}{\cos\theta}+a-\frac{\cos^2\theta}{\cos\theta} \\[5pt]
&=&
x\tan\theta-\frac{1}{\cos\theta}+a \\[5pt]
\end{eqnarray}となる。
この接線と $y=x^2$ との交点の $x$ 座標を $\alpha,\beta$ とすると、これらは\[ x^2-x\tan\theta+\frac{1}{\cos\theta}-a=0 \]の解なので
\begin{eqnarray}
\alpha+\beta=\tan\theta,\ \alpha\beta=\frac{1}{\cos\theta}-a
\end{eqnarray}が成り立つ。よって、
\begin{eqnarray}
L_{\mathrm{P}}^2
&=&
(\beta-\alpha)^2+(\beta^2-\alpha^2)^2 \\[5pt]
&=&
(\beta-\alpha)^2+(\beta-\alpha)^2(\beta+\alpha)^2 \\[5pt]
&=&
(\beta-\alpha)^2\{1+(\beta+\alpha)^2\} \\[5pt]
&=&
\{(\beta+\alpha)^2-4\alpha\beta\}(1+\tan^2\theta) \\[5pt]
&=&
\left\{\tan^2\theta-4\left(\frac{1}{\cos\theta}-a\right)\right\} \frac{1}{\cos^2\theta} \\[5pt]
&=&
\left( \frac{1-\cos^2\theta}{\cos^2\theta}-\frac{4}{\cos\theta}+4a\right) \frac{1}{\cos^2\theta} \\[5pt]
&=&
\frac{1}{\cos^4\theta} -\frac{1}{\cos^2\theta}-\frac{4}{\cos^3\theta}+\frac{4a}{\cos^2\theta} \\[5pt]
&=&
\frac{1}{\cos^4\theta}-\frac{4}{\cos^3\theta}+\frac{4a-1}{\cos^2\theta}
\end{eqnarray}となる。
求める範囲は、 $\theta$ を $0\leqq \theta\lt \dfrac{\pi}{2}$ の範囲で小さい値から大きな値に動かしたときに、ある値を2回以上とるような $a$ の範囲である。
ここで、 $t=\dfrac{1}{\cos\theta}$ とすると、 $t$ は $1$ 以上のすべての実数値をとる。また、 $\theta$ と $t$ は1対1に対応するので、 $t\geqq 1$ の範囲で動かしたときにある値を2回以上とるような $a$ の範囲を求めればよい。
最後の式を $t$ を使って表すと
\begin{eqnarray}
t^4-4t^3+(4a-1)t^2
\end{eqnarray}となる。この式を $f(t)$ とおくと
\begin{eqnarray}
f'(t) &=& 4t^3 -12t^2 +2t(4a-1) \\[5pt]
&=& 2t (2t^2 -6t +4a-1) \\[5pt]
\end{eqnarray}となる。 $2t^2 -6t +4a-1=0$ の判別式が正となるのは
\begin{eqnarray}
(-6)^2-4\cdot 2\cdot(4a-1) & \gt & 0 \\[5pt]
9-2\cdot(4a-1) & \gt & 0 \\[5pt]
9-8a+2 & \gt & 0 \\[5pt]
a & \lt & \frac{11}{8} \\[5pt]
\end{eqnarray}のときである。このときの実数解は\[ t=\frac{3\pm\sqrt{11-8a}}{2} \]であり、少なくとも片方は明らかに $1$ より大きい。
よって、 $\dfrac{5}{4} \lt a\lt \dfrac{11}{8}$ のときは、 $f'(t)$ は $\dfrac{3+\sqrt{11-8a}}{2}$ の前後で、負から正に変わるため、 $f(t)$ は $t\geqq 1$ の範囲で同じ値を2回以上とりうる。
一方、 $a\geqq \dfrac{11}{8}$ のときは、 $f'(t)$ は $t\geqq 1$ の範囲で正であり、 $f(t)$ は狭義単調増加なので、 $f(t)$ は同じ値をとることはない。
以上から、求める範囲は、 $\dfrac{5}{4} \lt a\lt \dfrac{11}{8}$ …(答)





