東京大学 理系 2006年度後期 第1問 解説
問題編
【問題】
xy平面上でtを変数とする媒介変数表示
\begin{eqnarray} \left\{ \begin{array}{l} x = 2t+t^2 \\ y = t+2t^2 \end{array} \right. \end{eqnarray}で表される曲線をCとする。 次の問に答えよ。(1) $t\ne -1$のとき、$\displaystyle \frac{dy}{dx}$をtの式で表せ。
(2) 曲線C上で\[ \frac{dy}{dx} = -\frac{1}{2} \]を満たす点Aの座標を求めよ。
(3) 曲線C上の点$(x,y)$を点$(X,Y)$に移す移動が
\begin{eqnarray} \left\{ \begin{array}{l} X = \frac{1}{\sqrt{5} }(2x-y) \\[5pt] Y = \frac{1}{\sqrt{5} }(x+2y) \end{array} \right. \end{eqnarray}で表されているとする。このときYをXを用いて表せ。(4) 曲線Cの概形をxy平面上に描け。
【考え方】
(1)(2)は基本的な問題です。(3)も代入すればきれいな式になるので難しくはありません。
(4)は(3)の変形が何なのかをまず考える必要があります。概形を描く際、放物線の頂点は出しておいた方がいいですが、実は(2)が使えます。(2)が使えることに気づかなくても計算すれば出せるので、それほど難しくはないでしょう。
解答編
【問題】
xy平面上でtを変数とする媒介変数表示
\begin{eqnarray} \left\{ \begin{array}{l} x = 2t+t^2 \\ y = t+2t^2 \end{array} \right. \end{eqnarray}で表される曲線をCとする。 次の問に答えよ。(1) $t\ne -1$のとき、$\displaystyle \frac{dy}{dx}$をtの式で表せ。
(2) 曲線C上で\[ \frac{dy}{dx} = -\frac{1}{2} \]を満たす点Aの座標を求めよ。
【解答】
(1)
$\displaystyle \frac{dx}{dt}=2+2t$、$\displaystyle \frac{dy}{dt}=1+4t$なので、\[ \frac{dy}{dx} = \frac{1+4t}{2+2t} \]となる。
(2)
\begin{eqnarray}
\frac{1+4t}{2+2t} &=& -\frac{1}{2} \\[5pt]
1+4t &=& -(1+t) \\[5pt]
5t &=& -2 \\[5pt]
t &=& -\frac{2}{5} \\[5pt]
\end{eqnarray}となる。
このとき、
\begin{eqnarray}
x = -\frac{2\cdot2}{5} +\left(-\frac{2}{5}\right)^2 = -\frac{16}{25}
\end{eqnarray}であり、
\begin{eqnarray}
y=-\frac{2}{5}+2\left(-\frac{2}{5}\right)^2=-\frac{2}{25}
\end{eqnarray}なので、点Aの座標は、$\displaystyle \left(-\frac{16}{25}, -\frac{2}{25}\right)$となる。
【解答終】
【問題】
(3) 曲線C上の点$(x,y)$を点$(X,Y)$に移す移動が
\begin{eqnarray} \left\{ \begin{array}{l} X = \frac{1}{\sqrt{5} }(2x-y) \\[5pt] Y = \frac{1}{\sqrt{5} }(x+2y) \end{array} \right. \end{eqnarray}で表されているとする。このときYをXを用いて表せ。
【解答】
(3)
\begin{eqnarray}
X
&=&
\frac{1}{\sqrt{5} }(2x-y) \\[5pt]
&=&
\frac{1}{\sqrt{5} }\{2(2t+t^2)-(t+2t^2)\} \\[5pt]
&=&
\frac{3t}{\sqrt{5} } \\
\end{eqnarray}なので、$\displaystyle t=\frac{\sqrt{5} }{3}X$である。
また、
\begin{eqnarray}
Y
&=&
\frac{1}{\sqrt{5} }(x+2y) \\[5pt]
&=&
\frac{1}{\sqrt{5} }\{ (2t+t^2) +2(t+2t^2) \} \\[5pt]
&=&
\frac{1}{\sqrt{5} }(5t^2 +4t) \\[5pt]
\end{eqnarray}なので、$\displaystyle t=\frac{\sqrt{5} }{3}X$を代入すると、
\begin{eqnarray}
Y
&=&
\frac{1}{\sqrt{5} }(5t^2 +4t) \\[5pt]
&=&
\frac{1}{\sqrt{5} }\left( 5\cdot\frac{5}{9}X^2 +4\cdot\frac{\sqrt{5} }{3}X \right) \\[5pt]
&=&
\frac{5\sqrt{5} }{9}X^2 +\frac{4}{3}X
\end{eqnarray}となる。
【解答終】
【問題】
(4) 曲線Cの概形をxy平面上に描け。
【解答】
(4)
$\cos\theta=\frac{2}{\sqrt{5} }$、$\sin\theta=\frac{1}{\sqrt{5} }$となる$\theta$は、$0\leqq \theta \lt 2\pi$の範囲で1つだけ存在する。これを用いると、\[ X+iY=(x+iy)(\cos\theta +i\sin\theta) \]となることがわかる。(3)より$\displaystyle Y=\frac{5\sqrt{5} }{9}X^2 +\frac{4}{3}X$だから、曲線Cは、この放物線を原点について$-\theta$回転したものになる。
この放物線の頂点での接線の傾きは0なので、これを$-\theta$回転した曲線Cの頂点では、接線の傾きは$\tan(-\theta) = -\frac{1}{2}$となる。これと(2)より、点Aが曲線Cの頂点であることがわかる。
$x=0$のとき、$t=0,-2$であり、yの値はそれぞれ$0,6$となる。また、$y=0$のとき、$t=0,-\frac{1}{2}$なので、xの値はそれぞれ$0,-\frac{3}{4}$となる。
以上から、曲線Cの概形は次のようになる。
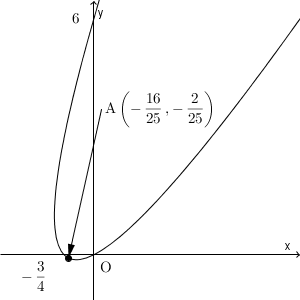
【解答終】
【解説】
(3)までは難しいところは特にありません。
(4)では、まず(3)が回転を表していることに気づく必要があります。また、回転によって、頂点の接線の傾きがどうなるかを考えれば、(2)の点Aが頂点だということもわかります。
ただ、(2)が使えることに気づくのは、少し難しいです。(2)の使い方に気づかなくても、XとYの式から頂点を求め、それを回転させることもできるので、手詰まりになることはないでしょう。時間のロスにはなりますが。





