東京大学 文系 2020年度 第2問 解説
問題編
問題
座標平面上に8本の直線
\begin{eqnarray} x &=& a \ (a=1,2,3,4), \\ y &=& b \ (b=1,2,3,4) \end{eqnarray}がある。以下、16個の点\[ (a,b)\quad (a=1,2,3,4,\ b=1,2,3,4) \]から異なる5個の点を選ぶことを考える。(1) 次の条件を満たす5個の点の選ぶ方は何通りあるか。
上の8本の直線のうち、選んだ点を1個も含まないものがちょうど2本ある。
(2) 次の条件を満たす5個の点の選び方は何通りあるか。
上の8本の直線は、いずれも選んだ点を少なくとも1個含む。
考え方
大変ですが、どう計算してもたくさん場合分けをして考えなくてはいけません。ある程度グループ化して簡略化するようにしましょう。(1)ができなくても(2)ができるかもしれないので、どちらにも挑戦してみましょう。
解答編
問題
座標平面上に8本の直線
\begin{eqnarray} x &=& a \ (a=1,2,3,4), \\ y &=& b \ (b=1,2,3,4) \end{eqnarray}がある。以下、16個の点\[ (a,b)\quad (a=1,2,3,4,\ b=1,2,3,4) \]から異なる5個の点を選ぶことを考える。(1) 次の条件を満たす5個の点の選ぶ方は何通りあるか。
上の8本の直線のうち、選んだ点を1個も含まないものがちょうど2本ある。
解答
(1)
選んだ点を含まない直線をはじめから除外し、残りのどの直線も、選んだ点を少なくとも1個含むような場合を考えることにする。
(i) 横の2本、または、縦の2本を除外する場合
まずは、横の2本を除外する場合を考える。なお、除外する方法は ${}_4\mathrm{C}_2=6$ 通りである。
直線を除外した後は、次の図のようになっている。
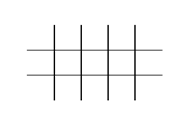
このときに、選んだ5点がどの直線の上にも乗るような場合を考える。このとき、縦の各直線について、選んだ点を含む個数は、 $2,1,1,1$ の並び替えになっている。 $2$ の場所の選び方は4通りある。このとき、横の直線は選んだ点を1個は含むため、残りの3点はそれぞれ上の直線か下の直線かを自由に選べる。
以上から、横の2本を除外する場合の点の選び方は\[ 6\times 4\times 2^3=192 \]通りである。縦の2本を除外する場合も同様なので、(i)の場合の数は 384 通りである。
(ii) 縦と横の直線を1本ずつ除外する場合
直線を除外する方法は $4\times 4=16$ 通りである。直線を除外した後は、次の図のようになっている。
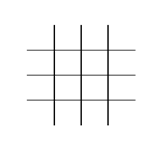
以下では、選んだ5点がどの直線にも乗るような場合を考える。このとき、縦の各直線について、選んだ点を含む個数は、 $1,2,2$ の並び替えか、 $3,1,1$ の並び替えになっている。
まず $3,1,1$ の場合を考える。 $3$ の場所の選び方は $3$ 通りである。残りの1点の選び方は、それぞれ3通り自由に決めることができる。そのため、\[ 3\times 3\times 3=27 \]通りである。
次に $1,2,2$ の場合を考える。 $1$ の場所の選び方は3通りある。このとき、左側の2個の点の場所を考える。この決め方は ${}_3\mathrm{C}_2=3$ 通りである。もし、右側の2個の点が左側の2個の点と同じ直線を選んだ場合は、残りの1個の点の場所は自動的に1か所に決まる。
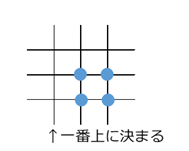
一方、右側の2個の点と左側の2個の点について、含まれている直線が一致しない場合は、残りの1個の点の場所は3か所のうち、どこでもよい。
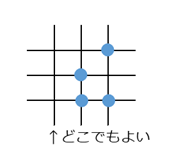
右側の2個の点を含む直線が、左側の2個の点を含む直線と一致しない場合は2通りある。
以上から、この場合の点の選び方は\[ 3\times 3\times(1\times 1+2\times 3)=63 \]通りである。
よって、(ii)の場合の点の選び方は\[ 16\times(27+63)=1440 \]通りである。
(i)(ii)から、\[ 384+1440=1824 \]通りと求められる。
(終)
解答編 つづき
問題
(2) 次の条件を満たす5個の点の選び方は何通りあるか。
上の8本の直線は、いずれも選んだ点を少なくとも1個含む。
解答
選んだ5点がどの直線にも含まれるような選び方を考える。
縦の各直線に点がいくつ含まれているかを数えると、 $2,1,1,1$ の並び替えになる。 $2$ の場所の選び方は $4$ 通りで、この直線上のどの2点を選ぶかは ${}_4\mathrm{C}_2=6$ 通りある。
残りの3つある1点の選び方を考える。このうち、2点が同じ横の直線に含まれているとする。このとき、残りの1点の場所は1つに決まる。
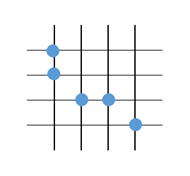
どの2点が同じ横の直線に含まれているかが3通り、どの横の直線に含まれているかが2通りあるので、6通りの選び方がある。
また、3つある1点のうち、縦に2点を含む直線上の点のどちらかと同じ横の直線に含まれている場合を考える。このような1点の選び方は3通りあり、2点のどちらと同じ横の直線に含まれるかが2通りある。また、残った2つの1点は選び方は2通りある。
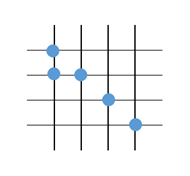
よって、このときの選び方は\[ 3\times 2 \times 2=12 \]通りである。
2点を含む縦の直線を選び、その2点の場所を選ぶたびに、残りの3点を選ぶ方法が $6+12=18$ 通りあるため、求める場合の数は\[ 4\times 6\times 18=432 \]通りとなる。
(終)





