東京大学 文系 2015年度 第3問 解説
問題編
【問題】
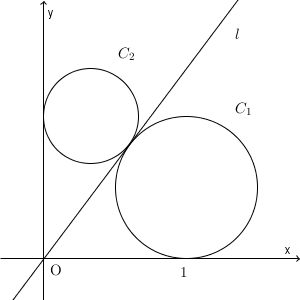
lを座標平面上の原点を通り傾きが正の直線とする。さらに、以下の3条件(i)、(ii)、(iii)で定まる円$C_1$, $C_2$を考える。(i) 円$C_1$, $C_2$は2つの不等式 $x\geqq 0$, $y\geqq 0$ で定まる領域に含まれる。
(ii) 円$C_1$, $C_2$は直線lと同一点で接する。
(iii) 円$C_1$はx軸と点$(1,0)$で接し、円$C_2$はy軸と接する。円$C_1$の半径を$r_1$、円$C_2$の半径を$r_2$とする。$8r_1+9r_2$が最小となるような直線lの方程式と、その最小値を求めよ。
【考え方】
まずは、$r_1$を使って、$r_2$をどう表せばいいかを考えます。いくつか方法はありますが、ここでは$\tan$の加法定理を使います(解答後に別の出し方も書きます)。
問題は$8r_1+9r_2$の評価です。分母に変数が来てしまうので、その最小値を求めるのが難しいです。使える道具は少ないので、いかに「例の技」に持ち込むかがポイントになってきます。
解答編
【問題】
lを座標平面上の原点を通り傾きが正の直線とする。さらに、以下の3条件(i)、(ii)、(iii)で定まる円$C_1$, $C_2$を考える。(i) 円$C_1$, $C_2$は2つの不等式 $x\geqq 0$, $y\geqq 0$ で定まる領域に含まれる。
(ii) 円$C_1$, $C_2$は直線lと同一点で接する。
(iii) 円$C_1$はx軸と点$(1,0)$で接し、円$C_2$はy軸と接する。円$C_1$の半径を$r_1$、円$C_2$の半径を$r_2$とする。$8r_1+9r_2$が最小となるような直線lの方程式と、その最小値を求めよ。
【解答】
円$C_1,C_2$の中心をそれぞれ$O_1,O_2$とする。円$C_1$と$x$軸との接点、$C_1$と$C_2$との接点、$C_2$と$y$軸との接点を、それぞれ$P,Q,R$とする。また、$\angle O_1OP$を$\theta$とする。

このとき、$r_1=\tan\theta$となる。$OP=OQ=OR=1$で$\angle O_2OR=\frac{\pi}{4}-\theta$なので
\begin{eqnarray}
r_2
&=&
\tan \left( \frac{\pi}{4}-\theta \right) \\[5pt]
&=&
\frac{\tan \frac{\pi}{4} -\tan \theta }{ 1 + \tan \frac{\pi}{4} \tan \theta } \\[5pt]
&=&
\frac{ 1 -r_1 }{ 1 + r_1 } \\[5pt]
&=&
-1 + \frac{ 2 }{ 1 + r_1 }
\end{eqnarray}となる。
よって、
\begin{eqnarray}
8r_1+9r_2
&=&
8r_1 + 9 \left( -1 + \frac{ 2 }{ 1 + r_1 } \right) \\
&=&
8(1+r_1)-8 -9 + \frac{ 18 }{ 1 + r_1 } \\[5pt]
&=&
8(1+r_1) + \frac{ 18 }{ 1 + r_1 } -17
\end{eqnarray}
ここで、相加相乗平均の関係より
\begin{eqnarray}
& &
8(1+r_1) + \frac{ 18 }{ 1 + r_1 } -17 \\[5pt]
&\geqq&
2\sqrt{ 8(1+r_1) \cdot \frac{ 18 }{ 1 + r_1 } } -17 \\[5pt]
&=&
2\sqrt{ 8 \cdot 18 } -17 = 7
\end{eqnarray}となる。
等号が成り立つのは、
\begin{eqnarray}
8(1+r_1) &=& \frac{ 18 }{ 1 + r_1 } \\[5pt]
(1+r_1)^2 &=& \frac{ 18 }{ 8 } \\[5pt]
1+r_1 &=& \pm \frac{ 3 }{ 2 } \\[5pt]
r_1 &=& \frac{ 1 }{ 2 }, -\frac{ 5 }{ 2 } \\
\end{eqnarray}
のとき。$r_1\gt 0$なので $r_1=\frac{1}{2}$のときとなる。
よって、$r_1=\frac{1}{2}$のとき、$8r_1+9r_2$は最小値7をとる。
また、直線$l$の傾きは $\tan 2\theta$なので、このときの傾きは
\begin{eqnarray}
\tan 2\theta
&=& \frac{2\tan \theta}{1-\tan^2 \theta}
= \frac{2r_1}{1-r_1^2} \\[5pt]
&=& \frac{2\cdot (1/2)}{1-(1/2)^2}
= \frac{4}{3}
\end{eqnarray}
なので、直線$l$の方程式は、$\displaystyle y=\frac{4}{3}x$となる。
よって、直線$l$の方程式は$\displaystyle y=\frac{4}{3}x$、最小値は7となる。
【解答終】
【解説】
前半部分の、$r_2$を$r_1$で表す部分は、次のようにしてもいいです。
<別解($r_2$の算出部分のみ)>
$O_1$から$y$軸におろした垂線と$O_2$から$x$軸におろした垂線との交点を$S$とした場合、三角形$O_1O_2S$は直角三角形なので、
\begin{eqnarray}
O_1O_2^2 &=& O_1S^2 + O_2S^2 \\
(r_1+r_2)^2 &=& (1-r_2)^2 + (1-r_1)^2 \\[5pt]
r_1^2 + 2r_1r_2 + r_2^2 &=& r_2^2 - 2r_2 + 1 + r_2^1 - 2r_1 + 1 \\[5pt]
(r_1+1)r_2 &=& -r_1 + 1 \\
r_2 &=& \frac{ -r_1 + 1}{r_1+1}
\end{eqnarray}<別解終>
また、$l$の傾きを出すのは、$O_1O_2$と$l$が垂直に交わることを用いて、$O_1O_2$の傾きから算出してもいいですね。
相加相乗を使うところがこの問題で一番難しいところだと思います。解答にあるような使い方になれていないと、先に進めません。理系であれば、分母に変数が入っていても微分すればよく、力技で解けてしまいます。逆に、理系でこの問題を解いて、相加相乗を使うという発想を思いつける人は少ないんでしょう。