東京大学 文系 2014年度 第3問 解説
問題編
問題
座標平面の原点を O で表す。
線分 $y=\sqrt{3} x$ $(0\leqq x \leqq 2)$ 上の点 P と、線分 $y=-\sqrt{3} x$ $(-3 \leqq x \leqq 0)$ 上の点 Q が、線分 OP と線分 OQ の長さの和が $6$ となるように動く。このとき、線分 PQ の通過する領域を D とする。(1) s を $-3\leqq s \leqq 2$ をみたす実数とするとき、点 $(s,t)$ が D に入るような t の範囲を求めよ。
(2) D を図示せよ。
考え方
$x=s$ で切ったときに、断面がどうなるかを考えて領域を求める問題です。流れはよくあるものですが、計算が少しややこしく、細々した条件が抜けやすいので注意が必要です。(2)は(1)ができれば問題なくできるでしょう。
理系の第6問と似ていますが、微妙に条件が違っています。
解答編
問題
座標平面の原点を O で表す。
線分 $y=\sqrt{3} x$ $(0\leqq x \leqq 2)$ 上の点 P と、線分 $y=-\sqrt{3} x$ $(-3 \leqq x \leqq 0)$ 上の点 Q が、線分 OP と線分 OQ の長さの和が $6$ となるように動く。このとき、線分 PQ の通過する領域を D とする。(1) s を $-3\leqq s \leqq 2$ をみたす実数とするとき、点 $(s,t)$ が D に入るような t の範囲を求めよ。
(2) D を図示せよ。
解答
(1) P, Q の x 座標を、それぞれ、 p, q とする。このとき、 $\mathrm{ P }(p,\sqrt{3} p)$, $\mathrm{ Q }(q,-\sqrt{3} q)$ となる。

また、 $0\leqq p \leqq 2$, $-3\leqq q \leqq 0$ なので、線分 OP, OQ の長さは、それぞれ $2p$, $-2q$ となる。
条件より $\mathrm{ OP }+\mathrm{ OQ }=6$ なので
\begin{eqnarray}
2p-2q &=& 6 \\
q &=& p-3
\end{eqnarray}が成り立つ。 $-3 \leqq q \leqq 0$ より、 $-3 \leqq p-3 \leqq 0$ 、つまり、 $0 \leqq p \leqq 3$ を満たす。もともと $0\leqq p \leqq 2$ も満たすので、条件を満たすように PQ が動くとき、 p がとる値の範囲は\[ 0 \leqq p \leqq 2 \]となることがわかる。
直線 PQ の式は、次のようになる。
\begin{eqnarray}
y
&=&
\frac{\sqrt{3}p-(-\sqrt{3}q)}{p-q}(x-p)+\sqrt{3}p \\[5pt]
&=&
\frac{\sqrt{3}(2p-3)}{3}(x-p)+\sqrt{3}p \\[5pt]
\end{eqnarray}
点 $(s,t)$ が線分 PQ 上にあるとすると、 $q=p-3 \leqq s \leqq p$ から p の範囲は\[ s \leqq p \leqq s+3 \]となる。また、このとき、 s, t について次が成り立つ。
\begin{eqnarray}
t
&=&
\frac{\sqrt{3}(2p-3)}{3}(s-p)+\sqrt{3}p \\[5pt]
&=&
\sqrt{3} \left\{ -\frac{2}{3}p^2 + \left( \frac{2}{3}s+2 \right)p -s \right \} \\[5pt]
&=&
\sqrt{3} \left\{ -\frac{2}{3}\left\{ p^2 -\left( s+3 \right)p \right\} -s \right\} \\[5pt]
&=&
\sqrt{3} \left\{ -\frac{2}{3}\left( p -\frac{s+3}{2} \right)^2 +\frac{2}{3}\left(\frac{s+3}{2}\right)^2 -s \right\} \\[5pt]
&=&
\sqrt{3} \left\{ -\frac{2}{3}\left( p -\frac{s+3}{2} \right)^2 +\frac{s^2+9}{6} \right\} \\[5pt]
\end{eqnarray}
$s(-3\leqq s \leqq 2)$ を固定し、 p を動かしたときに、 t のとり得る範囲を求める。
まず、 $\displaystyle p=\frac{s+3}{2}$ となる場合を考える。 $\displaystyle s \leqq p \leqq s+3$ から、
\begin{eqnarray}
& &
s \leqq \frac{s+3}{2} \leqq s+3 \\[5pt]
& \iff &
2s \leqq s+3 \leqq 2s+6 \\[5pt]
& \iff &
-3 \leqq s \leqq 3 \\[5pt]
\end{eqnarray}となる。また、 $0 \leqq p \leqq 2$ から、
\begin{eqnarray}
& &
0 \leqq \frac{s+3}{2} \leqq 2 \\[5pt]
& \iff &
0 \leqq s+3 \leqq 4 \\[5pt]
& \iff &
-3 \leqq s \leqq 1 \\[5pt]
\end{eqnarray}なので、 $\displaystyle p=\frac{s+3}{2}$ となりえるのは、 $-3\leqq s \leqq 1$ のときであることがわかる。
また、$0 \leqq p \leqq 2$ と $s \leqq p \leqq s+3$ を同時に満たす範囲は、次の3つの場合にわかれる。
- $-3\leqq s \leqq -1$ のときは、 $0 \leqq p \leqq s+3$
- $-1\leqq s \leqq 0$ のときは、 $0 \leqq p \leqq 2$
- $0 \leqq s \leqq 2$ のときは、 $s \leqq p \leqq 2$
(i) $-3\leqq s \leqq -1$ のとき
p の動く範囲は $0 \leqq p \leqq s+3$ なので、 p, t の関係を表すグラフは、次のような形になる(横軸が p 軸、縦軸が t 軸)。
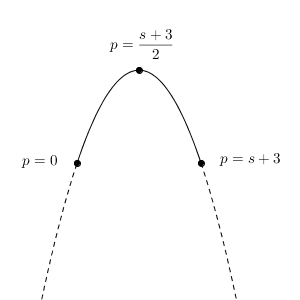
これより、 t は $\displaystyle p=\frac{s+3}{2}$ のとき、最大値 $\displaystyle \frac{\sqrt{3} }{6}(s^2+9)$ をとることがわかる。また、 $p=0,s+3$ のときに最小値をとり、その値は
\begin{eqnarray}
& &
-\sqrt{3} s \\[5pt]
\end{eqnarray}となる。また、 t はこの間の値をすべてとる。
(ii) $-1\lt s \leqq 0$ のとき
p の動く範囲は $0 \leqq p \leqq 2$ なので、 p, t の関係を表すグラフは、次のような形になる(横軸が p 軸、縦軸が t 軸)。
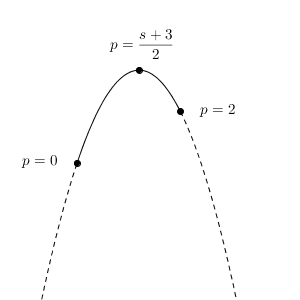
よって、 t は $\displaystyle p=\frac{s+3}{2}$ のとき、最大値 $\displaystyle \frac{\sqrt{3} }{6}(s^2+9)$ をとり、 $p=0$ のときに最小値 $-\sqrt{3} s$ をとることがわかる。また、 t はこの間の値をすべてとる。
(iii) $0\lt s \leqq 1$ のとき
p の動く範囲は $s \leqq p \leqq 2$ であり、 p, t の関係を表すグラフは、次のような形になる(横軸が p 軸、縦軸が t 軸)。
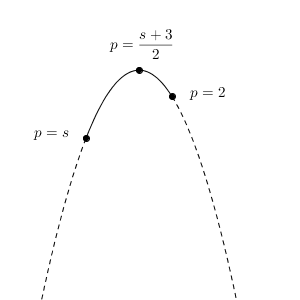
これより、 t は $\displaystyle p=\frac{s+3}{2}$ のとき、最大値 $\displaystyle \frac{\sqrt{3} }{6}(s^2+9)$ をとることがわかる。また、最小値は $p=s$ のときで、その値は
\begin{eqnarray}
& &
\sqrt{3} \left\{ -\frac{2}{3}s^2 + \left(\frac{2}{3}s+2\right)s -s \right\} \\[5pt]
&=&
\sqrt{3} s \\[5pt]
\end{eqnarray}となる。また、 t はこの間の値をすべてとる。
(iv) $1\lt s \leqq 2$ のとき
p の動く範囲は $s \leqq p \leqq 2$ であり、 p, t の関係を表すグラフは、次のような形になる(横軸が p 軸、縦軸が t 軸)。
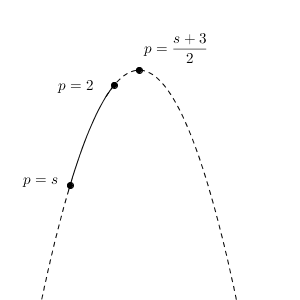
これより、 t は $p=2$ のときに最大値をとることがわかり、その値は
\begin{eqnarray}
& &
\sqrt{3} \left\{ -\frac{8}{3} + \left(\frac{2}{3}s+2\right)\times 2 -s \right\} \\[5pt]
&=&
\frac{\sqrt{3} }{3} ( s+4 ) \\[5pt]
\end{eqnarray}と計算できる。最小値は $p=s$ のときで、その値は(iii)のときと等しく $\sqrt{3}s$ である。また、 t はこの間の値をすべてとる。
(i)~(iv) より、求める範囲は、次の通りとなる。
$-3\leqq s \leqq 0$ のとき\[ -\sqrt{3} s \leqq t \leqq \frac{\sqrt{3} }{6}(s^2+9) \]
$0\lt s \leqq 1$ のとき\[ \sqrt{3} s \leqq t \leqq \frac{\sqrt{3} }{6}(s^2+9) \]
$1\lt s \leqq 2$ のとき\[ \sqrt{3} s \leqq t \leqq \frac{\sqrt{3} }{3} (s+4) \]
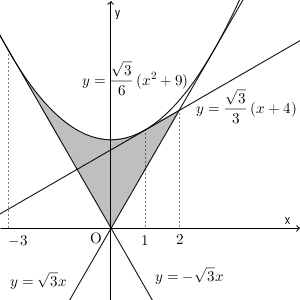
(2) (1)の結果から求める領域は下図の色のついた部分になる。ただし、境界線上の点をすべて含む。
解説
s を止めて p を動かし、 t の範囲を求める問題です。ただ、 p の範囲には少し注意が必要です。
p のとり得る範囲は、 $0\leqq p \leqq 2$ という条件のほかに、 $(s,t)$ が線分 PQ 上にあることから出てくる条件 $s\leqq p \leqq s+3$ もあります。さらに、 s, t に関する条件から出てくる二次関数は、 s の値によって最大・最小をとるときが変わることにも注意しないといけません。
ルートが出てきて計算しにくい上、条件式や場合分けも多く、ごちゃごちゃしてしまいがちです。流れは一般的ですが、計算間違いしやすいです。(2)は(1)ができればすぐにできますが、図をかいてみて、明らかな計算間違いをしていないか確認しましょう。





