共通テスト 数学II・数学B 2023年度追試 第4問 解説
【第3問~第5問から2問選択】
問題編
問題
数列の増減について考える。与えられた数列 $\{p_n\}$ の増減について次のように定める。
- すべての自然数 $n$ について $p_n \lt p_{n+1}$ となるとき、数列 $\{p_n\}$ はつねに増加するという。
- すべての自然数 $n$ について $p_n \gt p_{n+1}$ となるとき、数列 $\{p_n\}$ はつねに減少するという。
- $p_k\lt p_{k+1}$ となる自然数 $k$ があり、さらに $p_{\ell} \gt p_{\ell+1}$ となる自然数 $\ell$ もあるとき、数列 $\{p_n\}$ は増加することも減少することもあるという。
(1) 数列 $\{a_n\}$ は\[ a_1=23,\ a_{n+1}=a_n-3 \quad (n=1,2,3,\cdots) \]を満たすとする。このとき\[ a_n=\myBox{アイ}n+\myBox{ウエ} \quad (n=1,2,3,\cdots) \]となり、 $a_n\lt 0$ を満たす最小の自然数 $n$ は $\myBox{オ}$ である。
数列 $\{a_n\}$ は $\dBox{カ}$ 。また、自然数 $n$ に対して、 $\displaystyle S_n=\sum_{k=1}^n a_k$ とおくと、数列 $\{S_n\}$ は $\dBox{キ}$ 。
$n\geqq \mybox{オ}$ のとき、 $\dBox{ク}$ 。また、 $b_a=\dfrac{1}{a_n}$ とおくと、 $n\geqq \mybox{オ}$ のとき、 $\dBox{ケ}$ 。
$\dbox{カ}$, $\dbox{キ}$ の解答群(同じものを繰り返し選んでもよい。)
0: つねに増加する
1: つねに減少する
2: 増加することも減少することもある$\dbox{ク}$ の解答群
0: $a_n\lt 0$ である
1: $a_n\gt 0$ である
2: $a_n\lt 0$ となることも $a_n\gt 0$ となることもある$\dbox{ケ}$ の解答群
0: $b_n\lt b_{n+1}$ である
1: $b_n\gt b_{n+1}$ である
2: $b_n\lt b_{n+1}$ となることも $b_n\gt b_{n+1}$ となることもある(2) 数列 $\{c_n\}$ は\[ c_1=30,\ c_{n+1}=\frac{50c_n-800}{c_n-10} \quad (n=1,2,3,\cdots) \]を満たすとする。
以下では、すべての自然数 $n$ に対して $c_n\ne 20$ となることを用いてよい。
$d_n=\dfrac{1}{c_n-20}$ $(n=1,2,3,\cdots)$ とおくと、 $d_1=\dfrac{1}{\myBox{コサ}}$ であり、また\[ c_n=\dfrac{1}{d_n}+\myBox{シス} \quad (n=1,2,3,\cdots) \quad \cdots ① \]が成り立つ。したがって\[ \dfrac{1}{d_{n+1}} = \frac{50\left(\frac{1}{d_n}+\mybox{シス}\right)-800}{\left(\frac{1}{d_n}+\mybox{シス}\right)-10} -\mybox{シス} \ (n=1,2,3,\cdots) \]により\[ d_{n+1}=\dfrac{d_n}{\myBox{セ}}+\dfrac{1}{\myBox{ソタ}} \ (n=1,2,3,\cdots) \]が成り立つ。
数列 $\{d_n\}$ の一般項は\[ d_n=\dfrac{1}{\myBox{チツ}}\left(\frac{1}{\myBox{テ}}\right)^{n-1}+\frac{1}{\myBox{トナ}} \]である。
したがって、 $d_n\dBox{ニ}\dfrac{1}{\mybox{トナ}}$ $(n=1,2,3,\cdots)$ であり、数列 $\{d_n\}$ は $\dBox{ヌ}$ 。
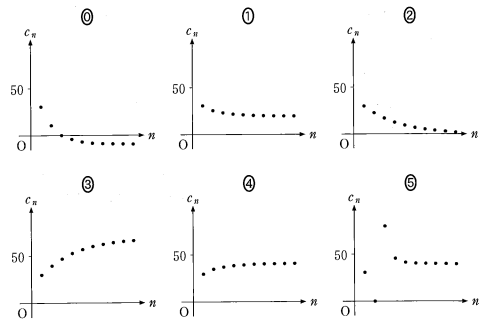
よって①により、 $\mathrm{O}$ を原点とする座標平面上に $n=1$ から $n=10$ まで点 $(n,c_n)$ を図示すると $\dBox{ネ}$ となる。
$\dbox{ニ}$ の解答群
0: $\lt$
1: $=$
2: $\gt$$\dbox{ヌ}$ の解答群
0: つねに増加する
1: つねに減少する
2: 増加することも減少することもある$\dbox{ネ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。
考え方
数列の増加・減少が問われることはあまりありませんが、一般項が求められればそんなに難しくはないでしょう。
後半はノーヒントは厳しいですが、誘導が丁寧なので、取り組みやすいです。分数の計算に慣れている必要はありますが、計算量はそれほど多くありません。
最後の図を選ぶ問題は、選ぶために必要な情報はすべてすでに求めてあります。グラフの「50」の使い方も、意味があります。
解答編
問題
数列の増減について考える。与えられた数列 $\{p_n\}$ の増減について次のように定める。
- すべての自然数 $n$ について $p_n \lt p_{n+1}$ となるとき、数列 $\{p_n\}$ はつねに増加するという。
- すべての自然数 $n$ について $p_n \gt p_{n+1}$ となるとき、数列 $\{p_n\}$ はつねに減少するという。
- $p_k\lt p_{k+1}$ となる自然数 $k$ があり、さらに $p_{\ell} \gt p_{\ell+1}$ となる自然数 $\ell$ もあるとき、数列 $\{p_n\}$ は増加することも減少することもあるという。
(1) 数列 $\{a_n\}$ は\[ a_1=23,\ a_{n+1}=a_n-3 \quad (n=1,2,3,\cdots) \]を満たすとする。このとき\[ a_n=\myBox{アイ}n+\myBox{ウエ} \quad (n=1,2,3,\cdots) \]となり、 $a_n\lt 0$ を満たす最小の自然数 $n$ は $\myBox{オ}$ である。
解説
(1)
数列 $\{a_n\}$ は初項が $23$ で公差が $-3$ の等差数列です。この数列の一般項は
\begin{eqnarray}
a_n
&=&
23-3(n-1) \\[5pt]
&=&
-3n+26
\end{eqnarray}となります。 $a_n\lt 0$ となるのは $-3n+26\lt 0$ のときであり、 $n\gt \dfrac{26}{3}$ のときなので、 $a_n\lt 0$ を満たす最小の自然数 $n$ は $9$ だとわかります。
解答
アイウエ:-326 (2点)
オ:9 (2点)
解答編 つづき
問題
数列 $\{a_n\}$ は $\dBox{カ}$ 。また、自然数 $n$ に対して、 $\displaystyle S_n=\sum_{k=1}^n a_k$ とおくと、数列 $\{S_n\}$ は $\dBox{キ}$ 。
$n\geqq \mybox{オ}$ のとき、 $\dBox{ク}$ 。また、 $b_a=\dfrac{1}{a_n}$ とおくと、 $n\geqq \mybox{オ}$ のとき、 $\dBox{ケ}$ 。
$\dbox{カ}$, $\dbox{キ}$ の解答群(同じものを繰り返し選んでもよい。)
0: つねに増加する
1: つねに減少する
2: 増加することも減少することもある$\dbox{ク}$ の解答群
0: $a_n\lt 0$ である
1: $a_n\gt 0$ である
2: $a_n\lt 0$ となることも $a_n\gt 0$ となることもある$\dbox{ケ}$ の解答群
0: $b_n\lt b_{n+1}$ である
1: $b_n\gt b_{n+1}$ である
2: $b_n\lt b_{n+1}$ となることも $b_n\gt b_{n+1}$ となることもある
解説
数列 $\{a_n\}$ は $3$ ずつ減っていくので、つねに減少することがわかります。一方、 $n$ 項目までの和である $S_n$ については、はじめのうちは正の数を足し、$9$ 項目から負の数を足すことになるので、増加することも減少することもあることがわかります。
$a_n=-3n+26$ なので $n\geqq 9$ のときは $a_n\lt 0$ となります。
一方、 $n\geqq 9$ のときは、 $a_n \gt a_{n+1}$ であり、両辺は負なので、正の数 $a_n a_{n+1}$ で両辺を割ると\[ \frac{1}{a_{n+1}} \gt \frac{1}{a_n} \]となります。つまり、 $b_n \lt b_{n+1}$ が成り立ちます。
解答
カ:1 (1点)
キ:2 (2点)
クケ:00 (2点)
解答編 つづき
問題
(2) 数列 $\{c_n\}$ は\[ c_1=30,\ c_{n+1}=\frac{50c_n-800}{c_n-10} \quad (n=1,2,3,\cdots) \]を満たすとする。
以下では、すべての自然数 $n$ に対して $c_n\ne 20$ となることを用いてよい。
$d_n=\dfrac{1}{c_n-20}$ $(n=1,2,3,\cdots)$ とおくと、 $d_1=\dfrac{1}{\myBox{コサ}}$ であり、また\[ c_n=\dfrac{1}{d_n}+\myBox{シス} \quad (n=1,2,3,\cdots) \quad \cdots ① \]が成り立つ。
解説
(2)
\[ d_1=\frac{1}{c_1-20}=\frac{1}{10} \]となります。また、
\begin{eqnarray}
d_n &=& \frac{1}{c_n-20} \\[5pt]
(c_n-20)d_n &=& 1 \\[5pt]
c_n d_n-20d_n &=& 1 \\[5pt]
c_n d_n &=& 1+20d_n \\[5pt]
c_n &=& \frac{1}{d_n}+20 \\[5pt]
\end{eqnarray}と変形できます。
解答
コサ:10 (1点)
シス:20 (2点)
解答編 つづき
問題
したがって\[ \dfrac{1}{d_{n+1}} = \frac{50\left(\frac{1}{d_n}+\mybox{シス}\right)-800}{\left(\frac{1}{d_n}+\mybox{シス}\right)-10} -\mybox{シス} \ (n=1,2,3,\cdots) \]により\[ d_{n+1}=\dfrac{d_n}{\myBox{セ}}+\dfrac{1}{\myBox{ソタ}} \ (n=1,2,3,\cdots) \]が成り立つ。
数列 $\{d_n\}$ の一般項は\[ d_n=\dfrac{1}{\myBox{チツ}}\left(\frac{1}{\myBox{テ}}\right)^{n-1}+\frac{1}{\myBox{トナ}} \]である。
解説
①を $\{c_n\}$ の漸化式に代入すると
\begin{eqnarray}
\frac{1}{d_{n+1}}+20 &=& \frac{50\left(\frac{1}{d_n}+20\right)-800}{\left(\frac{1}{d_n}+20\right)-10} \\[5pt]
\frac{1}{d_{n+1}} &=& \frac{\frac{50}{d_n}+200}{\frac{1}{d_n}+10}-20 \\[5pt]
&=& \frac{\frac{50}{d_n}+200-20\left(\frac{1}{d_n}+10\right)}{\frac{1}{d_n}+10} \\[5pt]
&=& \frac{\frac{30}{d_n}}{\frac{1}{d_n}+10} \\[5pt]
&=& \frac{30}{1+10d_n} \\[5pt]
\end{eqnarray}となります。逆数を考えて
\begin{eqnarray}
d_{n+1} &=& \frac{1+10d_n}{30} \\[5pt]
&=& \frac{d_n}{3}+\frac{1}{30} \\[5pt]
\end{eqnarray}が得られます。
ここで、 $x=\dfrac{x}{3}+\dfrac{1}{30}$ とすると $\dfrac{2}{3}x=\dfrac{1}{30}$ より $x=\dfrac{1}{20}$ なので
\begin{eqnarray}
d_{n+1}-\dfrac{1}{20} &=& \frac{d_n}{3}+\frac{1}{30}-\dfrac{1}{20} \\[5pt]
&=& \frac{d_n}{3}-\frac{1}{60} \\[5pt]
&=& \frac{1}{3}\left(d_n-\frac{1}{20}\right) \\[5pt]
\end{eqnarray}となります。ここで、\[ d_1-\dfrac{1}{20}=\frac{1}{10}-\frac{1}{20}=\frac{1}{20} \]なので、数列$\left\{d_n-\dfrac{1}{20}\right\}$ は初項が $\dfrac{1}{20}$ で公比が $\dfrac{1}{3}$ の等比数列なので
\begin{eqnarray}
d_n-\frac{1}{20} &=& \frac{1}{20}\cdot\left(\frac{1}{3}\right)^{n-1} \\[5pt]
d_n &=& \frac{1}{20}\left(\frac{1}{3}\right)^{n-1}+\frac{1}{20} \\[5pt]
\end{eqnarray}となります。
解答
セソタ:330 (2点)
チツテトナ:20320 (2点)
解答編 つづき
問題
したがって、 $d_n\dBox{ニ}\dfrac{1}{\mybox{トナ}}$ $(n=1,2,3,\cdots)$ であり、数列 $\{d_n\}$ は $\dBox{ヌ}$ 。
よって①により、 $\mathrm{O}$ を原点とする座標平面上に $n=1$ から $n=10$ まで点 $(n,c_n)$ を図示すると $\dBox{ネ}$ となる。
$\dbox{ニ}$ の解答群
0: $\lt$
1: $=$
2: $\gt$$\dbox{ヌ}$ の解答群
0: つねに増加する
1: つねに減少する
2: 増加することも減少することもある$\dbox{ネ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。
解説
\[ d_n = \frac{1}{20}\left(\frac{1}{3}\right)^{n-1}+\frac{1}{20} \gt \frac{1}{20} \]となります。また、 $\left(\dfrac{1}{3}\right)^{n-1}$ の部分はどんどん小さくなっていくので、数列 $\{d_n\}$ は、つねに減少することがわかります。
$d_n$ は正で、つねに減少することから、 $\dfrac{1}{d_n}$ はつねに増加します。よって、 $c_n=\dfrac{1}{d_n}+20$ もつねに増加します。このことから、グラフは3と4の2つに絞られます。
$d_n\gt \dfrac{1}{20}$ なので、 $c_n=\dfrac{1}{d_n}+20 \lt 20+20=40$ なので、50を超えている選択肢3は不適だとわかります。こうして、選択肢4が最も適当だといえます。
解答
ニヌ:21 (2点)
ネ:4 (2点)