共通テスト 数学II・数学B 2023年度追試 第2問 [1] 解説

【必答問題】

問題編

問題

　縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形の厚紙がある。この厚紙から容積が最大となる箱を作る。このとき、箱にふたがない場合とふたがある場合で容積の最大値がどう変わるかを調べたい。ただし、厚紙の厚さは考えず、作る箱の形を直方体とみなす。

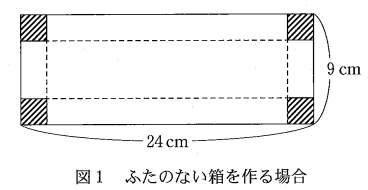
(1) 厚紙の四隅から図１にように四つの合同が正方形の斜線部分を切り取り、破線にそって折り曲げて、ふたのない箱を作る。この箱の容積を $V$ $\mathrm{cm}^3$ とする。

　次の構想に基づいて箱の容積の最大値を考える。

構想
　図１のように切り取る斜線部分の正方形の一辺の長さを $x$ $\mathrm{cm}$ とする。 $V$ を $x$ の関数として表し、箱が作れる $x$ の値の範囲に注意して $V$ の最大値を考える。

　箱が作れるための $x$ のとり得る値の範囲は $0\lt x\lt \dfrac{\myBox{ア}}{\myBox{イ}}$ である。 $V$ を $x$ の式で表すと\[ V=\myBox{ウ}x^3-\myBox{エオ}x^2+\myBox{カキク}x \]であり、 $V$ は $x=\myBox{ケ}$ で最大値 $\myBox{コサシ}$ をとる。

(2) 厚紙の四隅から図２のように四つの斜線部分を切り取り、破線にそって折り曲げて、ふたでぴったりと閉じることのできる箱を作る。この箱の容積を $W$ $\mathrm{cm}^3$ とする。

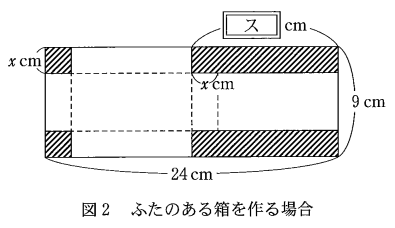
　図２の四つの斜線部分のうち、左側二つの斜線部分をそれぞれ一辺の長さが $x$ $\mathrm{cm}$ の正方形とすると、右側二つの斜線部分は、それぞれ縦の長さが $x$ $\mathrm{cm}$、横の長さが $\dBox{ス}$ $\mathrm{cm}$ の長方形となる。

$\dbox{ス}$ の解答群

　0: $6$
　1: $(6-x)$
　2: $(6+x)$

　3: $12$
　4: $(12-x)$
　5: $(12+x)$

　6: $18$
　7: $(18-x)$
　8: $(18+x)$

　太郎さんと花子さんは、 $W$ を $x$ の式で表した後、(1)の結果を見ながら $W$ の最大値の求め方について話している。

• $W$ の式がわかったから、 $W$ の最大値は(1)と同じように求められるね。
• ちょっと待って。$W$ を表す式と(1)の $V$ を表す式は似ているね。 $W$ を表す式と $V$ を表す式の関係を利用できないかな。

　(1)の $V$ が最大値をとるときの $x$ の値を $x_0$ とする。 $W$ の最大値は(1)で求めた $V$ の最大値 $\dBox{セ}$ 。また、 $W$ が最大値をとる $x$ は $\dBox{ソ}$ 。

$\dbox{セ}$ の解答群

　0: の $\dfrac{1}{4}$ 倍である
　1: の $4$ 倍である
　2: の $\dfrac{1}{3}$ 倍である
　3: の $3$ 倍である
　4: の $\dfrac{1}{2}$ 倍である
　5: の $2$ 倍である
　6: と等しくなる

$\dbox{ソ}$ の解答群

　0: ただ一つあり、その値は $x_0$ より小さい
　1: ただ一つあり、その値は $x_0$ より大きい
　2: ただ一つあり、その値は $x_0$ と等しい
　3: 二つ以上ある

(3) 縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形に限らず、いろいろな長方形の厚紙から(1),(2)と同じようにふたのない箱とふたのある箱を作る。このとき

　ふたのある箱の容積の最大値が、ふたのない箱の容積の最大値 $\dbox{セ}$

ということが成り立つための長方形についての記述として、次の 0 ～ 4 のうち、正しいものは $\dBox{タ}$ である。

$\dbox{タ}$ の解答群

　0: 縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形のときのみ成り立つ。
　1: 縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形のときと、縦の長さが $24$ $\mathrm{cm}$、横の長さが $9$ $\mathrm{cm}$ の長方形のときのみ成り立つ。
　2: 縦と横の長さの比が $3:8$ の長方形のときのみ成り立つ。
　3: 縦と横の長さの比が $3:8$ の長方形のときと、縦と横の長さの比が $8:3$ の長方形のときのみ成り立つ。
　4: 縦と横の長さに関係なくどのような長方形のときでも成り立つ。

考え方

前半は微分でよくある計算の問題です。後半は微分というよりは、関数の扱いを問う問題です。最後は抽象的すぎて、どう考えればいいかわかりづらいかもしれませんが、縦と横を文字で置いて考えてみるといいでしょう。

【必答問題】

解答編

問題

　縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形の厚紙がある。この厚紙から容積が最大となる箱を作る。このとき、箱にふたがない場合とふたがある場合で容積の最大値がどう変わるかを調べたい。ただし、厚紙の厚さは考えず、作る箱の形を直方体とみなす。

(1) 厚紙の四隅から図１にように四つの合同が正方形の斜線部分を切り取り、破線にそって折り曲げて、ふたのない箱を作る。この箱の容積を $V$ $\mathrm{cm}^3$ とする。

　次の構想に基づいて箱の容積の最大値を考える。

構想
　図１のように切り取る斜線部分の正方形の一辺の長さを $x$ $\mathrm{cm}$ とする。 $V$ を $x$ の関数として表し、箱が作れる $x$ の値の範囲に注意して $V$ の最大値を考える。

　箱が作れるための $x$ のとり得る値の範囲は $0\lt x\lt \dfrac{\myBox{ア}}{\myBox{イ}}$ である。 $V$ を $x$ の式で表すと\[ V=\myBox{ウ}x^3-\myBox{エオ}x^2+\myBox{カキク}x \]であり、 $V$ は $x=\myBox{ケ}$ で最大値 $\myBox{コサシ}$ をとる。

解説

四隅から正方形をとるときに、できるだけ大きく切り取ろうとすると、縦の長さがネックになります。 $2x\lt 9$ が成り立たないといけないので、\[ x\lt\frac{9}{2} \]となります。$x$ が正で、これを満たしていれば、正方形を切り取ることができます。

このときの体積は
\begin{eqnarray} V &=& (9-2x)(24-2x)x \\[5pt] &=& (4x^2-66x+216)x \\[5pt] &=& 4x^3-66x^2+216x \\[5pt] \end{eqnarray}となります。

$f(x)=4x^3-66x^2+216x$ とすると、 $f'(x)=12x^2-132x+216$ となります。 $f'(x)=0$ となるのは
\begin{eqnarray} 12x^2-132x+216&=&0 \\[5pt] x^2-11x+18&=&0 \\[5pt] (x-2)(x-9)&=&0 \\[5pt] x&=&2,9 \end{eqnarray}のときです。これより、増減表は次のようになります。 \begin{array}{c|ccccc} x & 0 & \cdots & 2 & \cdots & \frac{9}{2} \\ \hline f'(x) & & + & 0 & - & \\ \hline f(x) & & \nearrow & & \searrow & & \end{array}

こうして、 $x=2$ のときに $V$ が最大になることがわかります。そのときの値は
\begin{eqnarray} f(2) &=& 4\cdot 2^3-66\cdot 2^2+216\cdot 2 \\[5pt] &=& 32-264+432 \\[5pt] &=& 200 \\[5pt] \end{eqnarray} ともとめられます。

解答

解答編　つづき

問題

(2) 厚紙の四隅から図２のように四つの斜線部分を切り取り、破線にそって折り曲げて、ふたでぴったりと閉じることのできる箱を作る。この箱の容積を $W$ $\mathrm{cm}^3$ とする。

　図２の四つの斜線部分のうち、左側二つの斜線部分をそれぞれ一辺の長さが $x$ $\mathrm{cm}$ の正方形とすると、右側二つの斜線部分は、それぞれ縦の長さが $x$ $\mathrm{cm}$、横の長さが $\dBox{ス}$ $\mathrm{cm}$ の長方形となる。

$\dbox{ス}$ の解答群

　0: $6$
　1: $(6-x)$
　2: $(6+x)$

　3: $12$
　4: $(12-x)$
　5: $(12+x)$

　6: $18$
　7: $(18-x)$
　8: $(18+x)$

解説

(2)
右側の斜線部分の横の長さは、ふたの横の長さと $x$ との和です。この２つ分が $24$ $\mathrm{cm}$ なので、右側の斜線部分の横の長さは $12$ $\mathrm{cm}$ となります。

なお、ふたの横の長さは $\dfrac{24-2x}{2}=12-x$ となります。

解答

ス：3 (2点)

解答編　つづき

問題

　太郎さんと花子さんは、 $W$ を $x$ の式で表した後、(1)の結果を見ながら $W$ の最大値の求め方について話している。

• $W$ の式がわかったから、 $W$ の最大値は(1)と同じように求められるね。
• ちょっと待って。$W$ を表す式と(1)の $V$ を表す式は似ているね。 $W$ を表す式と $V$ を表す式の関係を利用できないかな。

　(1)の $V$ が最大値をとるときの $x$ の値を $x_0$ とする。 $W$ の最大値は(1)で求めた $V$ の最大値 $\dBox{セ}$ 。また、 $W$ が最大値をとる $x$ は $\dBox{ソ}$ 。

$\dbox{セ}$ の解答群

　0: の $\dfrac{1}{4}$ 倍である
　1: の $4$ 倍である
　2: の $\dfrac{1}{3}$ 倍である
　3: の $3$ 倍である
　4: の $\dfrac{1}{2}$ 倍である
　5: の $2$ 倍である
　6: と等しくなる

$\dbox{ソ}$ の解答群

　0: ただ一つあり、その値は $x_0$ より小さい
　1: ただ一つあり、その値は $x_0$ より大きい
　2: ただ一つあり、その値は $x_0$ と等しい
　3: 二つ以上ある

解説

ふたの縦の長さは $9-2x$ で、横の長さは $12-x$ です。また、箱の高さは $x$ なので、体積 $W$ は
\begin{eqnarray} W &=& (9-2x)(12-x)x \\[5pt] &=& \frac{1}{2}(9-2x)(24-2x)x \\[5pt] &=& \frac{V}{2} \\[5pt] \end{eqnarray}となります。よって、 $V$ が最大値をとるときの $x$ も、 $W$ が最大値をとるときの $x$ も同じ値です。また、 $W$ の最大値は $V$ の最大値の $\dfrac{1}{2}$ になることもわかります。

解答

セ：4 (3点)
ソ：2 (3点)

解答編　つづき

問題

(3) 縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形に限らず、いろいろな長方形の厚紙から(1),(2)と同じようにふたのない箱とふたのある箱を作る。このとき

　ふたのある箱の容積の最大値が、ふたのない箱の容積の最大値 $\dbox{セ}$

ということが成り立つための長方形についての記述として、次の 0 ～ 4 のうち、正しいものは $\dBox{タ}$ である。

$\dbox{タ}$ の解答群

　0: 縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形のときのみ成り立つ。
　1: 縦の長さが $9$ $\mathrm{cm}$、横の長さが $24$ $\mathrm{cm}$ の長方形のときと、縦の長さが $24$ $\mathrm{cm}$、横の長さが $9$ $\mathrm{cm}$ の長方形のときのみ成り立つ。
　2: 縦と横の長さの比が $3:8$ の長方形のときのみ成り立つ。
　3: 縦と横の長さの比が $3:8$ の長方形のときと、縦と横の長さの比が $8:3$ の長方形のときのみ成り立つ。
　4: 縦と横の長さに関係なくどのような長方形のときでも成り立つ。

解説

厚紙の縦と横の長さを $2a,2b$ としたとき、ふたのない箱の体積は\[ (2a-2x)(2b-2x)x \]となります。また、ふたのある箱の場合、ふたの横の長さは $b-x$ となるので、体積は\[ (2a-2x)(b-x)x \]となります。 $x$ のとる範囲は同じで、体積を表す式を見ると、ふたのない場合を $\dfrac{1}{2}$ 倍したものがふたのある場合になるので、最大値の比はつねに一定です。なので、縦と横の長さに関係なくどのような長方形のときでも成り立つことがわかります。

解答

タ：4 (4点)