共通テスト 数学II・数学B 2022年度追試 第5問 解説
【第3問~第5問から2問選択】
問題編
問題
$a$ を正の実数とする。O を原点とする座標空間に4点
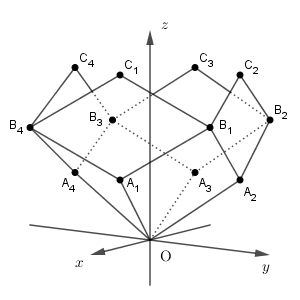
\begin{eqnarray} & & \mathrm{ A }_1(1,0,a), \mathrm{ A }_2(0,1,a), \\[5pt] & & \mathrm{ A }_3(-1,0,a), \mathrm{ A }_4(0,-1,a) \\[5pt] \end{eqnarray}がある。また、次の図のように、4点 $\mathrm{ B }_1,\mathrm{ B }_2,\mathrm{ B }_3,\mathrm{ B }_4$ を四角形 $\mathrm{ A_1OA_2B_1 }$, $\mathrm{ A_2OA_3B_2 }$, $\mathrm{ A_3OA_4B_3 }$, $\mathrm{ A_4OA_1B_4 }$ がそれぞれひし形になるようにとる。さらに、4点 $\mathrm{ C_1,C_2,C_3,C_4 }$ を四角形 $\mathrm{ A_1B_1C_1B_4 }$, $\mathrm{ A_2B_2C_2B_1 }$, $\mathrm{ A_3B_3C_3B_2 }$, $\mathrm{ A_4B_4C_4B_3 }$ がそれぞれひし形になるようにとる。ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
(1) 点 $\mathrm{ B_2, C_3 }$ の座標は
\begin{eqnarray} & & \mathrm{ B_2 } \left( -1,\myBox{ア},\myBox{イウ} \right), \\[5pt] & & \mathrm{ C_3 } \left( -1,\myBox{エ},\myBox{オカ} \right) \end{eqnarray}である。また、
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=\dBox{キ}\ , \\[5pt] & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ B_2C_3 } }=\dBox{ク} \end{eqnarray}となる。$\dbox{キ}$, $\dbox{ク}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $1$
2: $-1$3: $a^2$
4: $a^2+1$
5: $a^2-1$6: $2a^2$
7: $2a^2+1$
8: $2a^2-1$(2) ひし形 $\mathrm{ A_1OA_2B_1 }$ と $\mathrm{ A_1B_1C_1B_4 }$ が合同であるとする。
対応する対角線の長さが等しいことから、 $a=\dfrac{\sqrt{\myBox{ケ} }}{\myBox{コ} }$ であることがわかる。
直線 $\mathrm{ OA_1 }$ 上に点 P を $\angle \mathrm{ OPA_2 }$ が直角となるようにとる。
実数 $s$ を用いて $\overrightarrow{ \mathrm{ OP } }=s\overrightarrow{ \mathrm{ OA_1 } }$ と表せる。 $\overrightarrow{ \mathrm{ PA_2 } }$ と $\overrightarrow{ \mathrm{ OA_1 } }$ が垂直であること、および
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_1 } } =\dfrac{\myBox{サ} }{\myBox{シ} }\ , \\[5pt] & & \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_2 } } =\dfrac{\myBox{ス} }{\myBox{セ} } \end{eqnarray}であることにより\[ s=\dfrac{\myBox{ソ} }{\myBox{タ} } \]であることがわかる。(3) 実数 $a$ および点 P を(2)のようにとり、3点 $\mathrm{ P, A_2,A_4 }$ を通る平面を $\alpha$ とするとき、次のことについて考察しよう。
考察すること 平面 $\alpha$ と2点 $\mathrm{ B_2, C_3 }$ の位置関係$\angle \mathrm{ OPA_4 }$ も直角であるので、 $\overrightarrow{ \mathrm{ OA_1 } }$ と平面 $\alpha$ は垂直であることに注意する。
直線 $\mathrm{ B_2C_3 }$ と平面 $\alpha$ の交点を Q とする。
実数 $t$ を用いて\[ \overrightarrow{ \mathrm{ OQ } }=\overrightarrow{ \mathrm{ OB_2 } }+t\overrightarrow{ \mathrm{ B_2C_3 } } \]と表せる。 $\overrightarrow{ \mathrm{ PQ } }$ が $\overrightarrow{ \mathrm{ OA_1 } }$ と垂直であることにより\[ t=\dBox{チ} \]であることがわかる。
座標空間から平面 $\alpha$ を除いた部分は、 $\alpha$ を境に、原点 O を含む側と含まない側に分けられる。このとき、点 $\mathrm{ B_2 }$ は $\dBox{ツ}$ にあり、点 $\mathrm{ C_3 }$ は $\dBox{テ}$ にある。
$\dbox{チ}$ の解答群
0: $0$
1: $1$
2: $-1$
3: $\dfrac{1}{2}$
4: $-\dfrac{1}{2}$
5: $\dfrac{1}{3}$
6: $-\dfrac{1}{3}$
7: $\dfrac{2}{3}$
$\dbox{ツ}, \dbox{テ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\alpha$ 上
1: O を含む側
2: O を含まない側
考え方
見た目はめんどくさそうですが、それほど大変ではありません。ひし形がたくさんあるので、等しいベクトルもたくさんあります。これを利用して解いていきます。
計算量はそれほど多くありません。最後の位置を答える問題は、何を使って答えるのかが少しわかりづらいですが、片方がわかれば、もう片方は図を使って考えることもできるでしょう。
解答編
問題
$a$ を正の実数とする。O を原点とする座標空間に4点
\begin{eqnarray} & & \mathrm{ A }_1(1,0,a), \mathrm{ A }_2(0,1,a), \\[5pt] & & \mathrm{ A }_3(-1,0,a), \mathrm{ A }_4(0,-1,a) \\[5pt] \end{eqnarray}がある。また、次の図のように、4点 $\mathrm{ B }_1,\mathrm{ B }_2,\mathrm{ B }_3,\mathrm{ B }_4$ を四角形 $\mathrm{ A_1OA_2B_1 }$, $\mathrm{ A_2OA_3B_2 }$, $\mathrm{ A_3OA_4B_3 }$, $\mathrm{ A_4OA_1B_4 }$ がそれぞれひし形になるようにとる。さらに、4点 $\mathrm{ C_1,C_2,C_3,C_4 }$ を四角形 $\mathrm{ A_1B_1C_1B_4 }$, $\mathrm{ A_2B_2C_2B_1 }$, $\mathrm{ A_3B_3C_3B_2 }$, $\mathrm{ A_4B_4C_4B_3 }$ がそれぞれひし形になるようにとる。ただし、座標空間における四角形を考える際には、その四つの頂点が同一平面上にあるものとする。
(1) 点 $\mathrm{ B_2, C_3 }$ の座標は
\begin{eqnarray} & & \mathrm{ B_2 } \left( -1,\myBox{ア},\myBox{イウ} \right), \\[5pt] & & \mathrm{ C_3 } \left( -1,\myBox{エ},\myBox{オカ} \right) \end{eqnarray}である。
解説
四角形 $\mathrm{ A_2OA_3B_2 }$ はひし形なので、 $\overrightarrow{ \mathrm{ OA_3 } }=\overrightarrow{ \mathrm{ A_2B_2 } }$ です。よって
\begin{eqnarray}
\overrightarrow{ \mathrm{ OB_2 } }
&=&
\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ A_2B_2 } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ OA_3 } } \\[5pt]
&=&
(0,1,a)+(-1,0,a) \\[5pt]
&=&
(-1,1,2a) \\[5pt]
\end{eqnarray}となるので、 $\mathrm{ B_2 }$ の座標は $(-1,1,2a)$ です。
四角形 $\mathrm{ A_3B_3C_3B_2 }$ もひし形なので、 $\overrightarrow{ \mathrm{ B_2C_3 } }=\overrightarrow{ \mathrm{ A_3B_3 } }$ です。さらに、四角形 $\mathrm{ A_3OA_4B_3 }$ もひし形なので、 $\overrightarrow{ \mathrm{ A_3B_3 } }=\overrightarrow{ \mathrm{ OA_4 } }$ です。よって
\begin{eqnarray}
\overrightarrow{ \mathrm{ OC_3 } }
&=&
\overrightarrow{ \mathrm{ OB_2 } }+\overrightarrow{ \mathrm{ B_2C_3 } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OB_2 } }+\overrightarrow{ \mathrm{ OA_4 } } \\[5pt]
&=&
(-1,1,2a)+(0,-1,a) \\[5pt]
&=&
(-1,0,3a) \\[5pt]
\end{eqnarray}となるので、 $\mathrm{ C_3 }$ の座標は $(-1,0,3a)$ となります。
解答
アイウ:12a
エオカ:03a
解答編 つづき
問題
また、
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=\dBox{キ}\ , \\[5pt] & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ B_2C_3 } }=\dBox{ク} \end{eqnarray}となる。$\dbox{キ}$, $\dbox{ク}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $1$
2: $-1$3: $a^2$
4: $a^2+1$
5: $a^2-1$6: $2a^2$
7: $2a^2+1$
8: $2a^2-1$
解説
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } } \\[5pt] &=& (1,0,a)\cdot (-1,1,2a) \\[5pt] &=& 2a^2-1 \\[5pt] \end{eqnarray}となります。また、 $\overrightarrow{ \mathrm{ B_2C_3 } }=\overrightarrow{ \mathrm{ OA_4 } }$ なので、 \begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ B_2C_3 } } \\[5pt] &=& (1,0,a)\cdot (0,-1,a) \\[5pt] &=& a^2 \\[5pt] \end{eqnarray}となります。解答
キ:8
ク:3
解答編 つづき
問題
(2) ひし形 $\mathrm{ A_1OA_2B_1 }$ と $\mathrm{ A_1B_1C_1B_4 }$ が合同であるとする。
対応する対角線の長さが等しいことから、 $a=\dfrac{\sqrt{\myBox{ケ} }}{\myBox{コ} }$ であることがわかる。
解説
(1)と同様にすれば、 $\mathrm{ B_1 }$ の座標は $(1,1,2a)$ なので、線分 $\mathrm{ OB_1 }$ の長さは $\sqrt{1^2+1^2+(2a)^2}=\sqrt{4a^2+2}$ となります。また、線分 $\mathrm{ A_1A_2 }$ の長さは $\sqrt{2}$ です。よって、2つの対角線の長さは $\sqrt{4a^2+2}$ と $\sqrt{2}$ になります。
(1)と同じように $\mathrm{ C_1 }$ の座標は $(1,0,3a)$ と計算でき、 $\mathrm{ A_1 }$ の座標は $(1,0,a)$ だから、 $\mathrm{ A_1C_1 }$ の長さは $2a$ となります。
もし2つのひし形が合同なら、対応する対角線の長さも等しくなります。 $\sqrt{4a^2+2}\gt \sqrt{4a^2}=2a$ なので、 $2a=\sqrt{2}$ が成り立つことがわかり、 $a=\dfrac{\sqrt{2} }{2}$ と求めることができます。
ちなみに、 $\mathrm{ B_4 }(1,-1,a)$ となるので、もう一つの対角線の長さは $2$ となり、 $\sqrt{4a^2+2}$ と一致します。これより、たしかに、 $a=\dfrac{\sqrt{2} }{2}$ のときに2つのひし形は合同になることがわかります。
解答
ケコ:22
解答編 つづき
問題
直線 $\mathrm{ OA_1 }$ 上に点 P を $\angle \mathrm{ OPA_2 }$ が直角となるようにとる。
実数 $s$ を用いて $\overrightarrow{ \mathrm{ OP } }=s\overrightarrow{ \mathrm{ OA_1 } }$ と表せる。 $\overrightarrow{ \mathrm{ PA_2 } }$ と $\overrightarrow{ \mathrm{ OA_1 } }$ が垂直であること、および
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_1 } } =\dfrac{\myBox{サ} }{\myBox{シ} }\ , \\[5pt] & & \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_2 } } =\dfrac{\myBox{ス} }{\myBox{セ} } \end{eqnarray}であることにより\[ s=\dfrac{\myBox{ソ} }{\myBox{タ} } \]であることがわかる。
解説
\begin{eqnarray} \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_1 } } &=& (1,0,a)\cdot(1,0,a) \\[5pt] &=& 1+a^2 \\[5pt] &=& 1+\frac{1}{2}=\dfrac{3}{2} \end{eqnarray}であり、 \begin{eqnarray} \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_2 } } &=& (1,0,a)\cdot(0,1,a) \\[5pt] &=& a^2=\frac{1}{2} \end{eqnarray}となります。$\overrightarrow{ \mathrm{ PA_2 } }$ と $\overrightarrow{ \mathrm{ OA_1 } }$ が垂直であることから、内積は $0$ になります。内積は
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ PA_2 } } \cdot \overrightarrow{ \mathrm{ OA_1 } } \\[5pt]
&=&
(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OP } }) \cdot \overrightarrow{ \mathrm{ OA_1 } } \\[5pt]
&=&
(\overrightarrow{ \mathrm{ OA_2 } }-s\overrightarrow{ \mathrm{ OA_1 } }) \cdot \overrightarrow{ \mathrm{ OA_1 } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OA_2 } } -s\overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OA_1 } } \\[5pt]
&=&
\frac{1}{2} -s\cdot \frac{3}{2} \\[5pt]
&=&
\frac{1-3s}{2} \\[5pt]
\end{eqnarray}と計算できるので、これが $0$ となることから $s=\dfrac{1}{3}$ だとわかります。
解答
サシ:32
スセ:12
ソタ:13
解答編 つづき
問題
(3) 実数 $a$ および点 P を(2)のようにとり、3点 $\mathrm{ P, A_2,A_4 }$ を通る平面を $\alpha$ とするとき、次のことについて考察しよう。
考察すること 平面 $\alpha$ と2点 $\mathrm{ B_2, C_3 }$ の位置関係$\angle \mathrm{ OPA_4 }$ も直角であるので、 $\overrightarrow{ \mathrm{ OA_1 } }$ と平面 $\alpha$ は垂直であることに注意する。
直線 $\mathrm{ B_2C_3 }$ と平面 $\alpha$ の交点を Q とする。
実数 $t$ を用いて\[ \overrightarrow{ \mathrm{ OQ } }=\overrightarrow{ \mathrm{ OB_2 } }+t\overrightarrow{ \mathrm{ B_2C_3 } } \]と表せる。 $\overrightarrow{ \mathrm{ PQ } }$ が $\overrightarrow{ \mathrm{ OA_1 } }$ と垂直であることにより\[ t=\dBox{チ} \]であることがわかる。
座標空間から平面 $\alpha$ を除いた部分は、 $\alpha$ を境に、原点 O を含む側と含まない側に分けられる。このとき、点 $\mathrm{ B_2 }$ は $\dBox{ツ}$ にあり、点 $\mathrm{ C_3 }$ は $\dBox{テ}$ にある。
$\dbox{チ}$ の解答群
0: $0$
1: $1$
2: $-1$
3: $\dfrac{1}{2}$
4: $-\dfrac{1}{2}$
5: $\dfrac{1}{3}$
6: $-\dfrac{1}{3}$
7: $\dfrac{2}{3}$
$\dbox{ツ}, \dbox{テ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\alpha$ 上
1: O を含む側
2: O を含まない側
解説
(2)より、 $\overrightarrow{ \mathrm{ OP } }=\dfrac{1}{3}\overrightarrow{ \mathrm{ OA_1 } }$ です。
三角形 $\mathrm{ OPA_2 }$ と三角形 $\mathrm{ OPA_4 }$ は、対称性から合同であり、問題文にある通り、 $\angle \mathrm{ OPA_4 }$ は直角だとわかります。なので、問題文にある通り、 $\overrightarrow{ \mathrm{ OA_1 } }$ は平面 $\alpha$ は垂直になります。
P, Q はどちらも平面 $\alpha$ 上の点なので、 $\overrightarrow{ \mathrm{ PQ } }$ は $\overrightarrow{ \mathrm{ OA_1 } }$ と垂直です。なので、内積は $0$ です。ここで
\begin{eqnarray}
\overrightarrow{ \mathrm{ PQ } }
&=&
\overrightarrow{ \mathrm{ OQ } }-\overrightarrow{ \mathrm{ OP } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OB_2 } } +t\overrightarrow{ \mathrm{ B_2C_3 } }-\frac{1}{3} \overrightarrow{ \mathrm{ OA_1 } } \\[5pt]
&=&
(-1,1,2a) +t(0,-1,a)-\frac{1}{3} (1,0,a) \\[5pt]
&=&
\left(-\frac{4}{3}, 1-t, \frac{(5+3t)a}{3} \right) \\[5pt]
\end{eqnarray}となります。これより、内積は
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ PQ } }\cdot \overrightarrow{ \mathrm{ OA_1 } } \\[5pt]
&=&
\left(-\frac{4}{3}, 1-t, \frac{(5+3t)a}{3} \right) \cdot (1,0,a) \\[5pt]
&=&
-\frac{4}{3}+\frac{(5+3t)a^2}{3} \\[5pt]
&=&
-\frac{4}{3}+\frac{5+3t}{6} \\[5pt]
&=&
\frac{-3+3t}{6} \\[5pt]
\end{eqnarray}なので、内積が $0$ とすると $t=1$ と求められます。なお、3行目から4行目で、 $a=\dfrac{\sqrt{2} }{2}$ であることを使っています。
$t=1$ ということは、\[ \overrightarrow{ \mathrm{ OQ } }=\overrightarrow{ \mathrm{ OB_2 } }+\overrightarrow{ \mathrm{ B_2C_3 } }=\overrightarrow{ \mathrm{ OC_3 } } \]ということであり、 Q は $\mathrm{ C_3 }$ と一致している、ということです。つまり、点 $\mathrm{ C_3 }$ は平面 $\alpha$ 上にあることがわかります。
また、 $a=\dfrac{\sqrt{2} }{2}$ なので、(1)の後半より\[ \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=2a^2-1=0 \]だから、 $\overrightarrow{ \mathrm{ OB_2 } }$ は $\overrightarrow{ \mathrm{ OA_1 } }$ と垂直です。このことから、 $\alpha$ と $\overrightarrow{ \mathrm{ OB_2 } }$ は平行であることがわかります。よって、 $\mathrm{ B_2 }$ は平面 $\alpha$ に対して$\mathrm{ O }$ と同じ側にあることがわかります。
もしくは、 $\overrightarrow{ \mathrm{ A_4C_3 } }$ が平面 $\alpha$ 上にあることと、 $\overrightarrow{ \mathrm{ B_2C_3 } }=\overrightarrow{ \mathrm{ OA_4 } }$ であることから、 $\overrightarrow{ \mathrm{ OB_2 } }$ と平面 $\alpha$ が平行であることに着目して答えることもできます。
解答
チ:1
ツテ:10