共通テスト数学II・数学B 2022年度第5問解説

🕒 2022/01/17 🔄 2023/05/01

【第3問～第5問から2問選択】

問題編

問題

　平面上の点 O を中心とする半径 $1$ の円周上に、3点 A, B, C があり、 $\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } }=-\dfrac{2}{3}$ および $\overrightarrow{ \mathrm{ OC } }=-\overrightarrow{ \mathrm{ OA } }$ を満たすとする。 $t$ を $0\lt t \lt 1$ を満たす実数とし、線分 AB を $t:(1-t)$ に内分する点を P とする。また、直線 OP 上に点 Q をとる。

(1) $\cos\angle \mathrm{ AOB }=\dfrac{\myBox{アイ} }{\myBox{ウ} }$ である。

　また、実数 $k$ を用いて、 $\overrightarrow{ \mathrm{ OQ } }=k\overrightarrow{ \mathrm{ OP } }$ と表せる。したがって
\begin{eqnarray} \overrightarrow{ \mathrm{ OQ } } &=& \dBox{エ} \overrightarrow{ \mathrm{ OA } }+\dBox{オ} \overrightarrow{ \mathrm{ OB } } \quad \cdots ① \\[5pt] \overrightarrow{ \mathrm{ CQ } } &=& \dBox{カ} \overrightarrow{ \mathrm{ OA } }+\dBox{キ} \overrightarrow{ \mathrm{ OB } } \end{eqnarray}となる。
　$\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OP } }$ が垂直となるのは、 $t=\dfrac{\myBox{ク} }{\myBox{ケ} }$ のときである。

　$\dbox{エ}$ ～ $\dbox{キ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $kt$
　1: $(k-kt)$
　2: $(kt+1)$
　3: $(kt-1)$
　4: $(k-kt+1)$
　5: $(k-kt-1)$

　以下、 $t\ne\dfrac{\mybox{ク} }{\mybox{ケ} }$ とし、 $\angle \mathrm{ OCQ }$ が直角であるとする。

(2) $\angle \mathrm{ OCQ }$ が直角であることにより、(1)の $k$ は\[ k=\dfrac{\myBox{コ} }{\myBox{サ}t-\myBox{シ} } \quad\cdots ② \]となることがわかる。

　平面から直線 OA を除いた部分は、直線 OA を境に二つの部分に分けられる。そのうち、点 B を含む部分を $D_1$ 、含まない部分を $D_2$ とする。また、平面から直線 OB を除いた部分は、直線 OB を境に二つの部分に分けられる。そのうち、点 A を含む部分を $E_1$ 、含まない部分を $E_2$ とする。

　・ $0\lt t\lt \dfrac{\mybox{ク} }{\mybox{ケ} }$ ならば、点 Q は $\dBox{ス}$。

　・ $\dfrac{\mybox{ク} }{\mybox{ケ} }\lt t\lt 1$ ならば、点 Q は $\dBox{セ}$。

　$\dbox{ス}$, $\dbox{セ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $D_1$ に含まれ、かつ $E_1$ に含まれる
　1: $D_1$ に含まれ、かつ $E_2$ に含まれる
　2: $D_2$ に含まれ、かつ $E_1$ に含まれる
　3: $D_2$ に含まれ、かつ $E_2$ に含まれる

(3) 太郎さんと花子さんは、点 P の位置と $\left| \overrightarrow{ \mathrm{ OQ } } \right|$ の関係について考えている。

　$t=\dfrac{1}{2}$ のとき、①と②により、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\myBox{ソ} }$ とわかる。

$t\ne \dfrac{1}{2}$ のときにも、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\mybox{ソ} }$ となる場合があるかな。

$\left| \overrightarrow{ \mathrm{ OQ } } \right|$ を $t$ を用いて表して、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\mybox{ソ} }$ を満たす $t$ の値について考えればいいと思うよ。

計算が大変そうだね。

直線 OA に関して、 $t=\dfrac{1}{2}$ のときの点 Q と対称な点を R としたら、 $\left| \overrightarrow{ \mathrm{ OR } } \right|=\sqrt{\mybox{ソ} }$ となるよ。

$\overrightarrow{ \mathrm{ OR } }$ と $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OB } }$ を用いて表すことができれば、 $t$ の値が求められそうだね。

　直線 OA に関して、 $t=\dfrac{1}{2}$ のときの点 Q と対称な点を R とすると
\begin{eqnarray} \overrightarrow{ \mathrm{ CR } } &=& \myBox{タ} \overrightarrow{ \mathrm{ CQ } } \\[5pt] &=& \myBox{チ} \overrightarrow{ \mathrm{ OA } } +\myBox{ツ} \overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となる。
　$t\ne\dfrac{1}{2}$ のとき、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\mybox{ソ} }$ となる $t$ の値は $\dfrac{\myBox{テ} }{\myBox{ト} }$ である。

考え方

(2)以降は、図をかいて考えないと、何をやっているかがわかりにくいでしょう。(2)は、 $t$ によって図がどのように変わるかをよく考えましょう。

最後は、会話がヒントになっているものの、どのように解釈して利用するかは少し難しいです。

【第3問～第5問から2問選択】

解答編

問題

　平面上の点 O を中心とする半径 $1$ の円周上に、3点 A, B, C があり、 $\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } }=-\dfrac{2}{3}$ および $\overrightarrow{ \mathrm{ OC } }=-\overrightarrow{ \mathrm{ OA } }$ を満たすとする。 $t$ を $0\lt t \lt 1$ を満たす実数とし、線分 AB を $t:(1-t)$ に内分する点を P とする。また、直線 OP 上に点 Q をとる。

(1) $\cos\angle \mathrm{ AOB }=\dfrac{\myBox{アイ} }{\myBox{ウ} }$ である。

　また、実数 $k$ を用いて、 $\overrightarrow{ \mathrm{ OQ } }=k\overrightarrow{ \mathrm{ OP } }$ と表せる。したがって
\begin{eqnarray} \overrightarrow{ \mathrm{ OQ } } &=& \dBox{エ} \overrightarrow{ \mathrm{ OA } }+\dBox{オ} \overrightarrow{ \mathrm{ OB } } \quad \cdots ① \\[5pt] \overrightarrow{ \mathrm{ CQ } } &=& \dBox{カ} \overrightarrow{ \mathrm{ OA } }+\dBox{キ} \overrightarrow{ \mathrm{ OB } } \end{eqnarray}となる。
　$\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OP } }$ が垂直となるのは、 $t=\dfrac{\myBox{ク} }{\myBox{ケ} }$ のときである。

　$\dbox{エ}$ ～ $\dbox{キ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $kt$
　1: $(k-kt)$
　2: $(kt+1)$
　3: $(kt-1)$
　4: $(k-kt+1)$
　5: $(k-kt-1)$

解説

線分 OA, OB の長さは $1$ なので
\begin{eqnarray} \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } } &=& \left|\overrightarrow{ \mathrm{ OA } }\right| \left|\overrightarrow{ \mathrm{ OB } }\right|\cos\angle \mathrm{ AOB } \\[5pt] -\dfrac{2}{3} &=& 1\cdot 1\cos\angle \mathrm{ AOB } \\[5pt] \cos\angle \mathrm{ AOB } &=& -\dfrac{2}{3} \\[5pt] \end{eqnarray}となります。

また、\[ \overrightarrow{ \mathrm{ OP } }=(1-t)\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } } \]なので、
\begin{eqnarray} \overrightarrow{ \mathrm{ OQ } } &=& k\overrightarrow{ \mathrm{ OP } } \\[5pt] &=& (k-kt)\overrightarrow{ \mathrm{ OA } }+kt\overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となり、 \begin{eqnarray} \overrightarrow{ \mathrm{ CQ } } &=& \overrightarrow{ \mathrm{ OQ } }-\overrightarrow{ \mathrm{ OC } } \\[5pt] &=& \overrightarrow{ \mathrm{ OQ } }+\overrightarrow{ \mathrm{ OA } } \\[5pt] &=& (k-kt+1)\overrightarrow{ \mathrm{ OA } }+kt\overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となります。

$\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OP } }$ の内積を計算すると
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA } } \cdot \overrightarrow{ \mathrm{ OP } } \\[5pt] &=& \overrightarrow{ \mathrm{ OA } } \cdot \left((1-t)\overrightarrow{ \mathrm{ OA } }+t\overrightarrow{ \mathrm{ OB } }\right) \\[5pt] &=& (1-t) +t\cdot \left(-\dfrac{2}{3}\right) \\[5pt] &=& 1-\frac{5}{3}t \end{eqnarray}なので、 $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OP } }$ が垂直となるとき、つまり、内積が $0$ となるのは $t=\dfrac{3}{5}$ のときとわかります。

解答

アイウ：-23
エオ：10
カキ：40
クケ：35

解答編つづき

　以下、 $t\ne\dfrac{\mybox{ク} }{\mybox{ケ} }$ とし、 $\angle \mathrm{ OCQ }$ が直角であるとする。

(2) $\angle \mathrm{ OCQ }$ が直角であることにより、(1)の $k$ は\[ k=\dfrac{\myBox{コ} }{\myBox{サ}t-\myBox{シ} } \quad\cdots ② \]となることがわかる。

解説

$\angle \mathrm{ OCQ }$ が直角であることと $\overrightarrow{ \mathrm{ CO } }$ と $\overrightarrow{ \mathrm{ CQ } }$ との内積が $0$ になることは同値です。つまり、 $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ CQ } }$ の内積が $0$ です。内積を計算すると
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA } } \cdot \overrightarrow{ \mathrm{ CQ } } \\[5pt] &=& \overrightarrow{ \mathrm{ OA } } \cdot \left\{ (k-kt+1)\overrightarrow{ \mathrm{ OA } }+kt\overrightarrow{ \mathrm{ OB } } \right\} \\[5pt] &=& (k-kt+1)-\dfrac{2}{3}kt \\[5pt] &=& k-\dfrac{5}{3}kt+1 \\[5pt] \end{eqnarray}となるので、これが $0$ となります。よって、 \begin{eqnarray} k-\dfrac{5}{3}kt+1 &=& 0 \\[5pt] 3k-5kt+3 &=& 0 \\[5pt] (3-5t)k &=& -3 \\[5pt] \end{eqnarray}となります。ここで、 $t\ne \dfrac{3}{5}$ なので、\[ k=\dfrac{3}{5t-3} \]となることがわかります。

解答

コサシ：353

解答編つづき

　平面から直線 OA を除いた部分は、直線 OA を境に二つの部分に分けられる。そのうち、点 B を含む部分を $D_1$ 、含まない部分を $D_2$ とする。また、平面から直線 OB を除いた部分は、直線 OB を境に二つの部分に分けられる。そのうち、点 A を含む部分を $E_1$ 、含まない部分を $E_2$ とする。

　・ $0\lt t\lt \dfrac{\mybox{ク} }{\mybox{ケ} }$ ならば、点 Q は $\dBox{ス}$。

　・ $\dfrac{\mybox{ク} }{\mybox{ケ} }\lt t\lt 1$ ならば、点 Q は $\dBox{セ}$。

　$\dbox{ス}$, $\dbox{セ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $D_1$ に含まれ、かつ $E_1$ に含まれる
　1: $D_1$ に含まれ、かつ $E_2$ に含まれる
　2: $D_2$ に含まれ、かつ $E_1$ に含まれる
　3: $D_2$ に含まれ、かつ $E_2$ に含まれる

解説

図をかくと次のようになります。

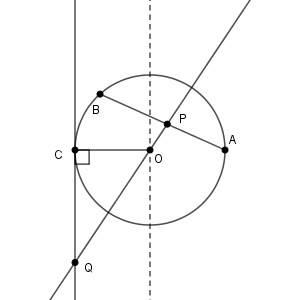
点 A, B, C は、中心が O で半径 $1$ の円周上の点です。破線は、 $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OP } }$ が垂直になる場合の直線 OP を表しています。

$0\lt t\lt\dfrac{3}{5}$ の場合、点 P は点 A に近い方に寄るので、 Q は上の図のようになります。よって、 Q は、 $D_2$ かつ $E_2$ に含まれることがわかります。

$\dfrac{3}{5}\lt t \lt 1$ の場合は、点 P は点 B に近い側に寄るので、次のような図になります。

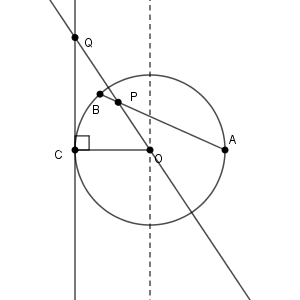
よって、 $D_1$ かつ $E_1$ に含まれることがわかります。

解答

ス：3
セ：0

解答編つづき

(3) 太郎さんと花子さんは、点 P の位置と $\left| \overrightarrow{ \mathrm{ OQ } } \right|$ の関係について考えている。

　$t=\dfrac{1}{2}$ のとき、①と②により、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\myBox{ソ} }$ とわかる。

解説

$t=\dfrac{1}{2}$ のとき、②より
\begin{eqnarray} k &=& \frac{3}{5t-3} = \frac{6}{10t-6} \\[5pt] &=& \frac{6}{5-6} = -6 \\[5pt] \end{eqnarray}となります。 $kt=-3$ なので、①より \begin{eqnarray} \overrightarrow{ \mathrm{ OQ } } &=& (k-kt)\overrightarrow{ \mathrm{ OA } }+kt\overrightarrow{ \mathrm{ OB } } \\[5pt] &=& (-6+3) \overrightarrow{ \mathrm{ OA } }-3\overrightarrow{ \mathrm{ OB } } \\[5pt] &=& -3 \overrightarrow{ \mathrm{ OA } } -3\overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となります。これより、 \begin{eqnarray} & & \left| \overrightarrow{ \mathrm{ OQ } } \right|^2 \\[5pt] &=& 9\left| \overrightarrow{ \mathrm{ OA } } \right|^2 +18\overrightarrow{ \mathrm{ OA } }\cdot\overrightarrow{ \mathrm{ OB } } +9\left| \overrightarrow{ \mathrm{ OB } } \right|^2 \\[5pt] &=& 9 -12 +9 \\[5pt] &=& 6 \end{eqnarray}となるので、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{6}$ となります。

解答

ソ：6

解答編つづき

$t\ne \dfrac{1}{2}$ のときにも、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\mybox{ソ} }$ となる場合があるかな。

$\left| \overrightarrow{ \mathrm{ OQ } } \right|$ を $t$ を用いて表して、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\mybox{ソ} }$ を満たす $t$ の値について考えればいいと思うよ。

計算が大変そうだね。

直線 OA に関して、 $t=\dfrac{1}{2}$ のときの点 Q と対称な点を R としたら、 $\left| \overrightarrow{ \mathrm{ OR } } \right|=\sqrt{\mybox{ソ} }$ となるよ。

$\overrightarrow{ \mathrm{ OR } }$ と $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OB } }$ を用いて表すことができれば、 $t$ の値が求められそうだね。

　直線 OA に関して、 $t=\dfrac{1}{2}$ のときの点 Q と対称な点を R とすると
\begin{eqnarray} \overrightarrow{ \mathrm{ CR } } &=& \myBox{タ} \overrightarrow{ \mathrm{ CQ } } \\[5pt] &=& \myBox{チ} \overrightarrow{ \mathrm{ OA } } +\myBox{ツ} \overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となる。
　$t\ne\dfrac{1}{2}$ のとき、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{\mybox{ソ} }$ となる $t$ の値は $\dfrac{\myBox{テ} }{\myBox{ト} }$ である。

解説

図は次のようになっています。

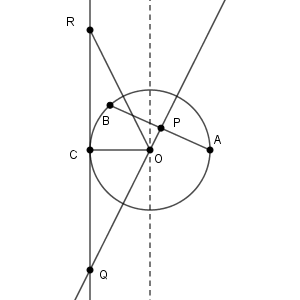
太郎さんと花子さんが言っているのは、上のように OR をひくと、線分 AB との交点ができるので、ここに P をもってくれば、 $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{6}$ となること、つまり、いま求めたいものがわかる、ということです。

R は直線 OA について点 Q と対称で、直線 OA と直線 CQ は垂直なので
\begin{eqnarray} \overrightarrow{ \mathrm{ CR } } &=& -\overrightarrow{ \mathrm{ CQ } } \\[5pt] &=& -(k-kt+1)\overrightarrow{ \mathrm{ OA } }-kt\overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となります。ここで、 $k=-6$, $kt=-3$ より \begin{eqnarray} \overrightarrow{ \mathrm{ CR } } &=& -(-6+3+1)\overrightarrow{ \mathrm{ OA } }+3\overrightarrow{ \mathrm{ OB } } \\[5pt] &=& 2\overrightarrow{ \mathrm{ OA } }+3\overrightarrow{ \mathrm{ OB } } \\[5pt] \end{eqnarray}となります。これより\[ \overrightarrow{ \mathrm{ OR } }=\overrightarrow{ \mathrm{ OC } }+\overrightarrow{ \mathrm{ CR } }=\overrightarrow{ \mathrm{ OA } }+3\overrightarrow{ \mathrm{ OB } } \]となることがわかります。

よって、線分 AB と線分 OR の交点を S とすると\[ \overrightarrow{ \mathrm{ OS } }=\frac{1}{4}\overrightarrow{ \mathrm{ OA } }+\frac{3}{4}\overrightarrow{ \mathrm{ OB } } \]となるので、 $t\ne\dfrac{1}{2}$ かつ $\left| \overrightarrow{ \mathrm{ OQ } } \right|=\sqrt{6}$ となる $t$ の値は $\dfrac{3}{4}$ と求められます。