共通テスト 数学II・数学B 2022年度 第4問 解説
【第3問~第5問から2問選択】
問題編
問題
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標が $y$ であるとき、その点は位置 $y$ にあるということにする。また、歩行者が自宅を出発してから $x$ 分経過した時点を時刻 $x$ と表す。歩行者は時刻 $0$ に自宅を出発し、正の向きに毎分 $1$ の速さで歩き始める。自転車は時刻 $2$ に自宅を出発し、毎分 $2$ の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分 $1$ の速さで歩き出し、自転車は毎分 $2$ の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分 $2$ の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
$x=a_n$ を自転車が $n$ 回目に自宅を出発する時刻とし、 $y=b_n$ をそのときの歩行者の位置とする。
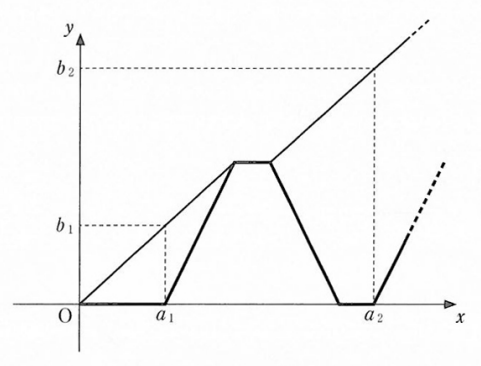
(1) 花子さんと太郎さんは、数列 $\{a_n\}$, $\{b_n\}$ の一般項を求めるために、歩行者と自転車について、時刻 $x$ において位置 $y$ にいることを $\mathrm{O}$ を原点とする座標平面上の点 $(x,y)$ で表すことにした。
$a_1=2$, $b_1=2$ により、自転車が最初に自宅を出発するときの時刻と自転車の位置を表す点の座標は $(2,0)$ であり、そのときの時刻と歩行者の位置を表す点の座標は $(2,2)$ である。また、自転車が最初に歩行者に追いつくときの時刻と位置を表す点の座標は $\left(\myBox{ア},\ \mybox{ア}\right)$ である。よって\[ a_2=\myBox{イ},\ b_2=\myBox{ウ} \]である。
- 数列 $\{a_n\}$, $\{b_n\}$ の一般項について考える前に、 $\left(\mybox{ア},\ \mybox{ア}\right)$ の求め方について整理してみようか。
- 花子さんはどうやって求めたの?
- 自転車が歩行者を追いかけるときに、間隔が1分間に $1$ ずつ縮まっていくことを利用したよ。
- 歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を計算して求めることもできるね。
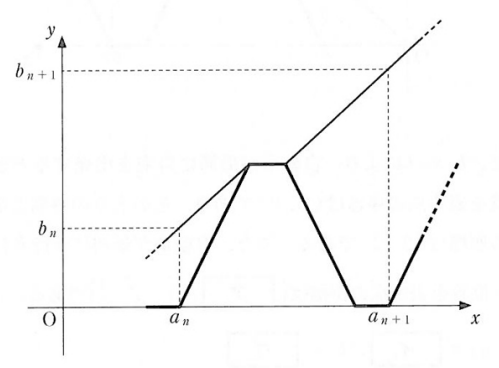
自転車が $n$ 回目に自宅を出発するときの時刻と自転車の位置を表す点の座標は $(a_n,0)$ であり、そのときの時刻と歩行者の位置を表す点の座標は $(a_n,b_n)$ である。よって、 $n$ 回目に自宅を出発した自転車が次に歩行者に追いつくときの時刻と位置を表す点の座標は、 $a_n,b_n$ を用いて、 $\left(\dBox{エ}, \dBox{オ}\right)$ と表せる。
$\dbox{エ}$, $\dbox{オ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $a_n$
1: $b_n$
2: $2a_n$
3: $a_n+b_n$
4: $2b_n$
5: $3a_n$
6: $2a_n+b_n$
7: $a_n+2b_n$
8: $3b_n$以上から、数列 $\{a_n\}$, $\{b_n\}$ について、自然数 $n$ に対して、関係式
\begin{eqnarray} a_{n+1} &=& a_n + \myBox{カ}b_n + \myBox{キ} \quad \cdots ① \\[5pt] b_{n+1} &=& 3b_n + \myBox{ク} \quad \cdots ② \end{eqnarray}が成り立つことがわかる。まず、 $b_1=2$ と②から\[ b_n=\dBox{ケ} \ (n=1,2,3,\cdots) \]を得る。この結果と、 $a_1=2$ および①から\[ a_n=\dBox{コ} \ (n=1,2,3,\cdots) \]がわかる。$\dbox{ケ}$, $\dbox{コ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $3^{n-1}+1$
1: $\dfrac{1}{2}\cdot3^{n}+\dfrac{1}{2}$2: $3^{n-1}+n$
3: $\dfrac{1}{2}\cdot3^{n}+n-\dfrac{1}{2}$4: $3^{n-1}+n^2$
5: $\dfrac{1}{2}\cdot3^{n}+n^2-\dfrac{1}{2}$6: $2\cdot 3^{n-1}$
7: $\dfrac{5}{2}\cdot3^{n-1}-\dfrac{1}{2}$8: $2\cdot 3^{n-1}+n-1$
9: $\dfrac{5}{2}\cdot3^{n-1}+n-\dfrac{3}{2}$a: $2\cdot 3^{n-1}+n^2-1$
b: $\dfrac{5}{2}\cdot3^{n-1}+n^2-\dfrac{3}{2}$(2) 歩行者が $y=300$ の位置に到着するときまでに、自転車が歩行者に追いつく回数は $\myBox{サ}$ 回である。また、 $\mybox{サ}$ 回目に自転車が歩行者に追いつく時刻は、 $x=\myBox{シスセ}$ である。
考え方
自転車の動きは謎ですが、動き方を把握するのは難しくはないでしょう。太郎さんと花子さんの会話は、なぜかアを解いた後にアのヒントになっているという変な配置になっています。グラフが間に挿入されていますが、大したヒントにはならないでしょう。
漸化式を作るところまでは、状況をきちんと把握していれば難しくはないでしょう。漸化式を解く計算は、今までのセンター試験などに比べるとかなり軽いです。数列の問題としてはよくある問題です。最後の問題も、最悪、力技でもなんとかなります。
【第3問~第5問から2問選択】
解答編
問題
以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車をその数直線上を動く点とみなす。数直線上の点の座標が $y$ であるとき、その点は位置 $y$ にあるということにする。また、歩行者が自宅を出発してから $x$ 分経過した時点を時刻 $x$ と表す。歩行者は時刻 $0$ に自宅を出発し、正の向きに毎分 $1$ の速さで歩き始める。自転車は時刻 $2$ に自宅を出発し、毎分 $2$ の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに1分だけ停止する。その後、歩行者は再び正の向きに毎分 $1$ の速さで歩き出し、自転車は毎分 $2$ の速さで自宅に戻る。自転車は自宅に到着すると、1分だけ停止した後、再び毎分 $2$ の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
$x=a_n$ を自転車が $n$ 回目に自宅を出発する時刻とし、 $y=b_n$ をそのときの歩行者の位置とする。
(1) 花子さんと太郎さんは、数列 $\{a_n\}$, $\{b_n\}$ の一般項を求めるために、歩行者と自転車について、時刻 $x$ において位置 $y$ にいることを $\mathrm{O}$ を原点とする座標平面上の点 $(x,y)$ で表すことにした。
$a_1=2$, $b_1=2$ により、自転車が最初に自宅を出発するときの時刻と自転車の位置を表す点の座標は $(2,0)$ であり、そのときの時刻と歩行者の位置を表す点の座標は $(2,2)$ である。また、自転車が最初に歩行者に追いつくときの時刻と位置を表す点の座標は $\left(\myBox{ア},\ \mybox{ア}\right)$ である。よって\[ a_2=\myBox{イ},\ b_2=\myBox{ウ} \]である。
- 数列 $\{a_n\}$, $\{b_n\}$ の一般項について考える前に、 $\left(\mybox{ア},\ \mybox{ア}\right)$ の求め方について整理してみようか。
- 花子さんはどうやって求めたの?
- 自転車が歩行者を追いかけるときに、間隔が1分間に $1$ ずつ縮まっていくことを利用したよ。
- 歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を計算して求めることもできるね。
解説
時刻 $2$ のときには、歩行者の位置は $2$ で、自転車の位置は $0$ です。距離は $2$ だけ離れています。
時刻が1分進むごとに、歩行者と自転車の距離は $2-1=1$ だけ縮まっていきます。なので、自転車が出発してから $2$ 分後に、自転車は歩行者に追いつきます。このことから、1回目に追いつくときの時刻は $2+2=4$ です。このときの歩行者の位置は $4$ です。
$1$ 分間停止をして、自転車は自宅に戻ります。距離 $4$ を毎分 $2$ のスピードで移動するので、 $2$ 分後には自宅に到着します。その $1$ 分後に自転車は自宅を出発することから、\[ a_2=4+1+2+1=8 \]となります。また、この間、歩行者は $1$ 分だけ停止をしているので、自宅からは $7$ 離れているから、 $b_2=7$ となります。
解答
ア:4
イ:8
ウ:7
解答編 つづき
自転車が $n$ 回目に自宅を出発するときの時刻と自転車の位置を表す点の座標は $(a_n,0)$ であり、そのときの時刻と歩行者の位置を表す点の座標は $(a_n,b_n)$ である。よって、 $n$ 回目に自宅を出発した自転車が次に歩行者に追いつくときの時刻と位置を表す点の座標は、 $a_n,b_n$ を用いて、 $\left(\dBox{エ}, \dBox{オ}\right)$ と表せる。
$\dbox{エ}$, $\dbox{オ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $a_n$
1: $b_n$
2: $2a_n$
3: $a_n+b_n$
4: $2b_n$
5: $3a_n$
6: $2a_n+b_n$
7: $a_n+2b_n$
8: $3b_n$
解説
自転車が $n$ 回目に自宅を出発するとき、時刻は $a_n$ です。自転車は自宅から $0$ の場所、歩行者は自宅から $b_n$ の場所にいます。
自転車と歩行者の距離は1分毎に $1$ ずつ縮まっていくので、 $b_n$ 分後に自転車は歩行者に追いつきます。そのため、追いついたときの時刻は $a_n+b_n$ と表すことができます。この間、歩行者は $b_n$ の位置から、毎分 $1$ の速さで $b_n$ 分間移動しているので、自宅から $b_n+b_n=2b_n$ だけ離れたところにいることがわかります。
解答
エ:3
オ:4
解答編 つづき
以上から、数列 $\{a_n\}$, $\{b_n\}$ について、自然数 $n$ に対して、関係式
\begin{eqnarray} a_{n+1} &=& a_n + \myBox{カ}b_n + \myBox{キ} \quad \cdots ① \\[5pt] b_{n+1} &=& 3b_n + \myBox{ク} \quad \cdots ② \end{eqnarray}が成り立つことがわかる。
解説
自転車が $n$ 回目に自宅を出発した後を考えます。前の問題で見たように、時刻 $a_n+b_n$ で自宅から $2b_n$ だけ離れた地点で歩行者に追いつきます。この後、自転車は $1$ 分停止して、時間 $2b_n\div 2=b_n$ だけかけて自宅に戻ります。この $1$ 分後に $n+1$ 回目の出発をするので、\[ a_{n+1}=(a_n+b_n)+1+b_n+1=a_n+2b_n+2 \]が成り立ちます。
また、歩行者は、時刻 $a_n$ から $a_{n+1}=a_n+2b_n+2$ の間、 $1$ 分停止する以外はずっと歩いているので\[ b_{n+1}=b_n+(2b_n+1)=3b_n+1 \]が成り立ちます。
解答
カキ:22
ク:1
解答編 つづき
まず、 $b_1=2$ と②から\[ b_n=\dBox{ケ} \ (n=1,2,3,\cdots) \]を得る。この結果と、 $a_1=2$ および①から\[ a_n=\dBox{コ} \ (n=1,2,3,\cdots) \]がわかる。
$\dbox{ケ}$, $\dbox{コ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $3^{n-1}+1$
1: $\dfrac{1}{2}\cdot3^{n}+\dfrac{1}{2}$2: $3^{n-1}+n$
3: $\dfrac{1}{2}\cdot3^{n}+n-\dfrac{1}{2}$4: $3^{n-1}+n^2$
5: $\dfrac{1}{2}\cdot3^{n}+n^2-\dfrac{1}{2}$6: $2\cdot 3^{n-1}$
7: $\dfrac{5}{2}\cdot3^{n-1}-\dfrac{1}{2}$8: $2\cdot 3^{n-1}+n-1$
9: $\dfrac{5}{2}\cdot3^{n-1}+n-\dfrac{3}{2}$a: $2\cdot 3^{n-1}+n^2-1$
b: $\dfrac{5}{2}\cdot3^{n-1}+n^2-\dfrac{3}{2}$
解説
$x=3x+1$ を解くと $x=-\dfrac{1}{2}$ なので\[ b_n+\dfrac{1}{2}=3 \left( b_n+\dfrac{1}{2} \right) \]が成り立ちます。よって、数列 $\left\{ b_n+\dfrac{1}{2} \right\}$ は、初項が $b_1+\dfrac{1}{2}=\dfrac{5}{2}$ で、公比が $3$ の等比数列なので
\begin{eqnarray}
b_n+\dfrac{1}{2} &=& \dfrac{5}{2}\cdot 3^{n-1} \\[5pt]
b_n &=& \dfrac{5}{2}\cdot 3^{n-1}-\dfrac{1}{2} \\[5pt]
\end{eqnarray}となります。
これを①に代入すると
\begin{eqnarray}
a_{n+1} &=& a_n +2b_n+2 \\[5pt]
&=& a_n +2\left( \dfrac{5}{2}\cdot 3^{n-1}-\dfrac{1}{2} \right)+2 \\[5pt]
&=& a_n +5\cdot 3^{n-1}+1 \\[5pt]
\end{eqnarray}となります。これより、 $n\geqq 2$ の場合は
\begin{eqnarray}
a_n
&=&
a_1 +\sum_{k=1}^{n-1} (5\cdot 3^{k-1}+1) \\[5pt]
&=&
2 + 5 \cdot\frac{3^{n-1}-1}{3-1} +(n-1) \\[5pt]
&=&
2+\frac{5}{2}\cdot 3^{n-1} -\frac{5}{2}+n-1 \\[5pt]
&=&
\frac{5}{2}\cdot 3^{n-1} +n-\frac{3}{2} \\[5pt]
\end{eqnarray}となります。 $n=1$ を代入すると最後の式は $2$ となるので、 $n=1$ のときも成り立ちます。よって、これが $a_n$ の一般項だとわかります。
解答
ケ:7
コ:9
解答編 つづき
(2) 歩行者が $y=300$ の位置に到着するときまでに、自転車が歩行者に追いつく回数は $\myBox{サ}$ 回である。また、 $\mybox{サ}$ 回目に自転車が歩行者に追いつく時刻は、 $x=\myBox{シスセ}$ である。
解説
歩行者が $y=300$ の位置に到着するとします。 $a_n\lt 300$ となる $n$ を考えると
\begin{eqnarray}
\frac{5}{2}\cdot 3^{n-1} +n-\frac{3}{2} & \lt & 300 \\[5pt]
3^{n-1} +\frac{2n}{5}-\frac{3}{5} & \lt & 120 \\[5pt]
3^n +\frac{6n}{5} & \lt & 360+\frac{9}{5}
\end{eqnarray}となります。代入して試していくと、 $n\leqq 5$ では成り立ちますが、 $n\geqq 6$ では成り立ちません。また、\[ b_5=\dfrac{5}{2}\cdot 3^{5-1}-\dfrac{1}{2}=202 \]となります。このことから、自転車の5回目の出発時点では、歩行者は自宅から $202$ のところにいるので、まだ $300$ の地点までは来ていないことがわかります。「5回目の出発」ということは、それまで4回歩行者に追いついていることがわかります。また、5回目に追いつくのは、オより、自宅から $2b_5=404$ だけ離れた地点なので、 $y=300$ を超えてしまいます。よって、自転車が歩行者に追いつくのは $4$ 回だとわかります。
\begin{eqnarray}
a_4 &=& \dfrac{5}{2}\cdot 3^{4-1} +4-\frac{3}{2} = 70 \\[5pt]
b_4 &=& \dfrac{5}{2}\cdot 3^{4-1}-\dfrac{1}{2}=67
\end{eqnarray}だから、4回目に追いつく時刻は、エより、 $a_4+b_4=137$ だとわかります。
解答
サ:4
シスセ:137