共通テスト 数学II・数学B 2022年度 第2問 [1] 解説

【必答問題】

問題編

問題

　$a$ を実数とし、 $f(x)=x^3-6ax+16$ とおく。

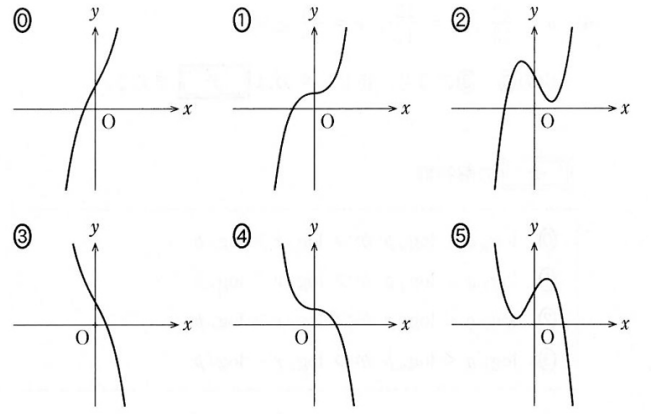
(1) $y=f(x)$ のグラフの概形は
　$a=0$ のとき、 $\dBox{ア}$
　$a\lt 0$ のとき、 $\dBox{イ}$
である。

　$\dbox{ア}$, $\dbox{イ}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

(2) $a\gt 0$ とし、 $p$ を実数とする。座標平面上の曲線 $y=f(x)$ と直線 $y=p$ が3個の共有点をもつような $p$ の値の範囲は $\dBox{ウ} \lt p \lt \dBox{エ}$ である。

　$p=\dbox{ウ}$ のとき、曲線 $y=f(x)$ と直線 $y=p$ は2個の共有点をもつ。それらの $x$ 座標を $q, r$ $(q\lt r)$ とする。曲線 $y=f(x)$ と直線 $y=p$ が点 $(r, p)$ で接することに注意すると\[ q=\myBox{オカ} \sqrt{\myBox{キ} } a^{\frac{1}{2} },\ r=\sqrt{\myBox{ク} } a^{\frac{1}{2} } \]と表せる。

　$\dbox{ウ}$, $\dbox{エ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $2\sqrt{2}a^{\frac{3}{2} }+16$
　1: $-2\sqrt{2}a^{\frac{3}{2} }+16$
　2: $4\sqrt{2}a^{\frac{3}{2} }+16$
　3: $-4\sqrt{2}a^{\frac{3}{2} }+16$
　4: $8\sqrt{2}a^{\frac{3}{2} }+16$
　5: $-8\sqrt{2}a^{\frac{3}{2} }+16$

(3) 方程式 $f(x)=0$ の異なる実数解の個数を $n$ とする。次の 0 ～ 5 のうち正しいものは $\dBox{ケ}$ と $\dBox{コ}$ である。

　$\dbox{ケ}$, $\dbox{コ}$ の解答群（解答の順序は問わない。）

　0: $n=1$ ならば $a\lt 0$
　1: $a\lt 0$ ならば $n=1$
　2: $n=2$ ならば $a\lt 0$
　3: $a\lt 0$ ならば $n=2$
　4: $n=3$ ならば $a\gt 0$
　5: $a\gt 0$ ならば $n=3$

考え方

微分とグラフの関係、グラフと方程式の関係を使う問題です。(2)の計算は、ヒントがついているのでそれを活用しましょう。(3)はグラフの形がどう変わるかを考えながら選ぶといいでしょう。

【必答問題】

解答編

問題

　$a$ を実数とし、 $f(x)=x^3-6ax+16$ とおく。

(1) $y=f(x)$ のグラフの概形は
　$a=0$ のとき、 $\dBox{ア}$
　$a\lt 0$ のとき、 $\dBox{イ}$
である。

　$\dbox{ア}$, $\dbox{イ}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

解説

$f'(x)=3x^2-6a$ です。

よって、 $a=0$ のときは $x=0$ のときに $f'(x)=0$ となり、 $x\ne 0$ のときは $f'(x)\gt 0$ となります。選択肢の中で該当するのは 1 です。

$a\lt 0$ のときは $f'(x)$ はつねに正なので、グラフは、選択肢の中では 0 となります。

解答

ア：1
イ：0

解答編 つづき

(2) $a\gt 0$ とし、 $p$ を実数とする。座標平面上の曲線 $y=f(x)$ と直線 $y=p$ が3個の共有点をもつような $p$ の値の範囲は $\dBox{ウ} \lt p \lt \dBox{エ}$ である。

　$p=\dbox{ウ}$ のとき、曲線 $y=f(x)$ と直線 $y=p$ は2個の共有点をもつ。それらの $x$ 座標を $q, r$ $(q\lt r)$ とする。曲線 $y=f(x)$ と直線 $y=p$ が点 $(r, p)$ で接することに注意すると\[ q=\myBox{オカ} \sqrt{\myBox{キ} } a^{\frac{1}{2} },\ r=\sqrt{\myBox{ク} } a^{\frac{1}{2} } \]と表せる。

　$\dbox{ウ}$, $\dbox{エ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $2\sqrt{2}a^{\frac{3}{2} }+16$
　1: $-2\sqrt{2}a^{\frac{3}{2} }+16$
　2: $4\sqrt{2}a^{\frac{3}{2} }+16$
　3: $-4\sqrt{2}a^{\frac{3}{2} }+16$
　4: $8\sqrt{2}a^{\frac{3}{2} }+16$
　5: $-8\sqrt{2}a^{\frac{3}{2} }+16$

解説

$f'(x)=3x^2-6a$ なので、$a\gt 0$ のときに $f'(x)=0$ とすると $x=\pm\sqrt{2a}$ となります。このことから、増減表は次のようになります。

また、 $x=\sqrt{2a}, -\sqrt{2a}$ を $f(x)=x^3-6ax+16$ に代入すると
\begin{eqnarray} f(\sqrt{2a}) &=& 2a\sqrt{2a}-6a\sqrt{2a}+16 \\[5pt] &=& -4 \sqrt{2} a^{\frac{3}{2} }+16 \\[5pt] \\ f(-\sqrt{2a}) &=& -2a\sqrt{2a}+6a\sqrt{2a}+16 \\[5pt] &=& 4 \sqrt{2} a^{\frac{3}{2} }+16 \\[5pt] \end{eqnarray}となります。よって、 $y=f(x)$ のグラフは次のようになります。

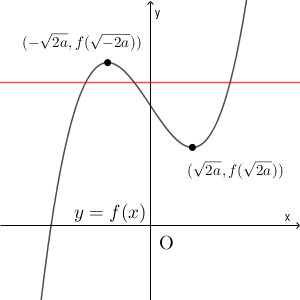
直線 $y=p$ （赤い線）を動かしたときに $y=f(x)$ との共有点が3個となるような $p$ の範囲は、 $f(\sqrt{2a})\lt p \lt f(-\sqrt{2a})$ なので、\[ -4 \sqrt{2} a^{\frac{3}{2} }+16\lt p \lt 4 \sqrt{2} a^{\frac{3}{2} }+16 \]となります。

$p=-4 \sqrt{2} a^{\frac{3}{2} }+16$ のとき、グラフは次のようになります。

まず、共有点の $x$ 座標のうち、大きい方は $r=\sqrt{2a}=\sqrt{2}a^{\frac{1}{2} }$ となります。もう片方を求めます。
\begin{eqnarray} f(x) &=& f(\sqrt{2a}) \\[5pt] x^3-6ax+16 &=& 4 \sqrt{2} a^{\frac{3}{2} }+16 \\[5pt] x^3-6ax+4 \sqrt{2} a^{\frac{3}{2} } &=& 0 \\[5pt] \end{eqnarray}これは $x=r$ を重解に持つので、左辺は $(x-r)^2=x^2-2\sqrt{2a}x+2a$ で割り切れます。割り算をすれば\[ (x-\sqrt{2a})^2 (x+2\sqrt{2a})=0 \]となることがわかるので、もう片方の $x$ 座標 $q$ は $-2\sqrt{2}a^{\frac{1}{2} }$ になることがわかります。

解答

ウ：3
エ：2
オカキ：-22
ク：2

解答編 つづき

(3) 方程式 $f(x)=0$ の異なる実数解の個数を $n$ とする。次の 0 ～ 5 のうち正しいものは $\dBox{ケ}$ と $\dBox{コ}$ である。

　$\dbox{ケ}$, $\dbox{コ}$ の解答群（解答の順序は問わない。）

　0: $n=1$ ならば $a\lt 0$
　1: $a\lt 0$ ならば $n=1$
　2: $n=2$ ならば $a\lt 0$
　3: $a\lt 0$ ならば $n=2$
　4: $n=3$ ならば $a\gt 0$
　5: $a\gt 0$ ならば $n=3$

解説

問題文の(1)のグラフの選択肢でいうと、 $a\lt 0$ が選択肢0 、 $a=0$ が選択肢1、 $a\gt 0$ が選択肢2　に対応します。

$a\leqq 0$ の場合は、グラフ $y=f(x)$ と $x$ 軸との交点は1つのみです。

(2)で考えた増減表からもわかる通り、 $a\gt 0$ のときの極小値はいくらでも小さくできます。そのため、 $y=f(x)$ のグラフは、 $a$ の値によって $x$ 軸との交点が1点、2点、3点になることがあります。どれか1つに決まるわけではありません。

このことから、 $n=1$ となるのは $a$ は正負いずれの場合もありえます。また、 $n=2$ や $n=3$ となるのは $a\gt 0$ のときだけです。よって、0, 2, 4の中では、4だけが正しいです。

また、 $a$ が負なら $n=1$ なので、1, 3, 5 の中では、1だけが正しいです。

解答

ケ・コ：1・4