共通テスト 数学I・数学A 2024年度 第5問 解説

【第3問～第5問から2問選択】

問題編

問題

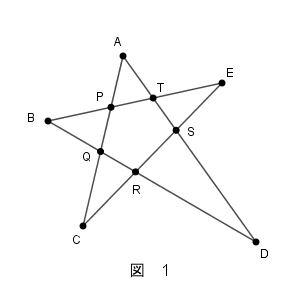
　図1のように、平面上に5点 $\mathrm{A,B,C,D,E}$ があり、線分 $\mathrm{AC}$, $\mathrm{CE}$, $\mathrm{EB}$, $\mathrm{BD}$, $\mathrm{DA}$ によって、星形の図形ができるときを考える。線分 $\mathrm{AC}$ と $\mathrm{BE}$ の交点を $\mathrm{P}$, $\mathrm{AC}$ と $\mathrm{BD}$ の交点を $\mathrm{Q}$, $\mathrm{BD}$ と $\mathrm{CE}$ の交点を $\mathrm{R}$, $\mathrm{AD}$ と $\mathrm{CE}$ の交点を $\mathrm{S}$, $\mathrm{AD}$ と $\mathrm{BE}$ の交点を $\mathrm{T}$ とする。

　ここでは
\begin{eqnarray} \mathrm{AP:PQ:QC}=2:3:3 \\[5pt] \mathrm{AT:TS:SD}=1:1:3 \\[5pt] \end{eqnarray}を満たす星形の図形を考える。

　以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

(1) $\triangle \mathrm{AQD}$ と直線 $\mathrm{CE}$ に着目すると\[ \dfrac{\mathrm{QR}}{\mathrm{RD}} \cdot \dfrac{\mathrm{DS}}{\mathrm{SA}} \cdot \dfrac{\dBox{ア}}{\mathrm{CQ}}=1 \]が成り立つので\[ \mathrm{QR:RD}=\myBox{イ}\ :\ \myBox{ウ} \]となる。また、$\triangle \mathrm{AQD}$ と直線 $\mathrm{BE}$ に着目すると\[ \mathrm{QB:BD}=\myBox{エ}\ :\ \myBox{オ} \]となる。したがって\[ \mathrm{BQ:QR:RD}=\mybox{エ}\ :\ \mybox{イ}\ :\ \mybox{ウ} \]となることがわかる。

　$\dbox{ア}$ の解答群

　0: $\mathrm{AC}$
　1: $\mathrm{AP}$
　2: $\mathrm{AQ}$
　3: $\mathrm{CP}$
　4: $\mathrm{PQ}$

(2) 5点 $\mathrm{P,Q,R,S,T}$ が同一円周上にあるとし、 $\mathrm{AC}=8$ であるとする。

(i) 5点 $\mathrm{A,P,Q,S,T}$ に着目すると、 $\mathrm{AT:AS}=1:2$ より $\mathrm{AT}=\sqrt{\myBox{カ}}$ となる。さらに、5点 $\mathrm{D,Q,R,S,T}$ に着目すると $\mathrm{DR}=4\sqrt{3}$ となることがわかる。

(ii) 3点 $\mathrm{A,B,C}$ を通る円と点 $\mathrm{D}$ との位置関係を、次の構想に基づいて調べよう。

構想
線分 $\mathrm{AC}$ と $\mathrm{BD}$ の交点 $\mathrm{Q}$ に着目し、 $\mathrm{AQ\cdot CQ}$ と $\mathrm{BQ\cdot DQ}$ の大小を比べる。

　まず、$\mathrm{AQ\cdot CQ}=5\cdot 3=15$ かつ $\mathrm{BQ\cdot DQ}=\myBox{キク}$ であるから\[ \mathrm{AQ\cdot CQ}\ \dBox{ケ}\ \mathrm{BQ\cdot DQ}\quad\cdots ① \]が成り立つ。また、3点 $\mathrm{A,B,C}$ を通る円と直線 $\mathrm{BD}$ との交点のうち、 $\mathrm{B}$ と異なる点を $\mathrm{X}$ とすると\[ \mathrm{AQ\cdot CQ}\ \dBox{コ}\ \mathrm{BQ\cdot XQ}\quad\cdots ② \]が成り立つ。①と②の左辺は同じなので、①と②の右辺を比べることにより、 $\mathrm{XQ}\ \dBox{サ}\ \mathrm{DQ}$ が得られる。したがって、点 $\mathrm{D}$ は3点 $\mathrm{A,B,C}$ を通る円の $\dBox{シ}$ にある。

　$\dbox{ケ}$ ～ $\dbox{サ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\lt$
　1: $=$
　2: $\gt$

　$\dbox{シ}$ の解答群

　0: 内部
　1: 周上
　2: 外部

(iii) 3点 $\mathrm{C,D,E}$ を通る円と2点 $\mathrm{A,B}$ との位置関係について調べよう。

　この星型の図形において、さらに $\mathrm{CR=RS=SE}=3$ となることがわかる。したがって、点 $\mathrm{A}$ は3点 $\mathrm{C,D,E}$ を通る円の $\dBox{ス}$ にあり、点 $\mathrm{B}$ は3点 $\mathrm{C,D,E}$ を通る円の $\dBox{ス}$ にある。

　$\dbox{ス}$, $\dbox{セ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 内部
　1: 周上
　2: 外部

考え方

図形の分野でよく出てくる定理を使って解いていきましょう。(2)(iii)は(ii)がヒントになっています。 $\mathrm{CR=RS=SE}=3$ という結果も書いてくれているので、かなり親切です。長さがいくらかだけでなく、その長さを使うことも読み取れるので、あとは(ii)の判定方法を真似するだけです。

【第3問～第5問から2問選択】

解答編

問題

　図1のように、平面上に5点 $\mathrm{A,B,C,D,E}$ があり、線分 $\mathrm{AC}$, $\mathrm{CE}$, $\mathrm{EB}$, $\mathrm{BD}$, $\mathrm{DA}$ によって、星形の図形ができるときを考える。線分 $\mathrm{AC}$ と $\mathrm{BE}$ の交点を $\mathrm{P}$, $\mathrm{AC}$ と $\mathrm{BD}$ の交点を $\mathrm{Q}$, $\mathrm{BD}$ と $\mathrm{CE}$ の交点を $\mathrm{R}$, $\mathrm{AD}$ と $\mathrm{CE}$ の交点を $\mathrm{S}$, $\mathrm{AD}$ と $\mathrm{BE}$ の交点を $\mathrm{T}$ とする。

　ここでは
\begin{eqnarray} \mathrm{AP:PQ:QC}=2:3:3 \\[5pt] \mathrm{AT:TS:SD}=1:1:3 \\[5pt] \end{eqnarray}を満たす星形の図形を考える。

　以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。

(1) $\triangle \mathrm{AQD}$ と直線 $\mathrm{CE}$ に着目すると\[ \dfrac{\mathrm{QR}}{\mathrm{RD}} \cdot \dfrac{\mathrm{DS}}{\mathrm{SA}} \cdot \dfrac{\dBox{ア}}{\mathrm{CQ}}=1 \]が成り立つので\[ \mathrm{QR:RD}=\myBox{イ}\ :\ \myBox{ウ} \]となる。また、$\triangle \mathrm{AQD}$ と直線 $\mathrm{BE}$ に着目すると\[ \mathrm{QB:BD}=\myBox{エ}\ :\ \myBox{オ} \]となる。したがって\[ \mathrm{BQ:QR:RD}=\mybox{エ}\ :\ \mybox{イ}\ :\ \mybox{ウ} \]となることがわかる。

　$\dbox{ア}$ の解答群

　0: $\mathrm{AC}$
　1: $\mathrm{AP}$
　2: $\mathrm{AQ}$
　3: $\mathrm{CP}$
　4: $\mathrm{PQ}$

解説

(1)

$\triangle \mathrm{AQD}$ と直線 $\mathrm{CE}$ についてメネラウスの定理を使うと
\begin{eqnarray} \frac{\mathrm{QR}}{\mathrm{RD}} \cdot \frac{\mathrm{DS}}{\mathrm{SA}} \cdot \frac{\mathrm{AC}}{\mathrm{CQ}} &=& 1 \end{eqnarray}が成り立ちます。ここで、仮定より $\mathrm{DS:SA}=3:(1+1)=3:2$ と $\mathrm{AC:CQ}=(2+3+3):3=8:3$ なので \begin{eqnarray} \frac{\mathrm{QR}}{\mathrm{RD}} \cdot \frac{3}{2} \cdot \frac{8}{3} &=& 1 \\[5pt] \frac{\mathrm{QR}}{\mathrm{RD}} &=& \frac{1}{4} \end{eqnarray}なので、$\mathrm{QR:RD}=1:4$ となります。

また、$\triangle \mathrm{AQD}$ と直線 $\mathrm{BE}$ についてメネラウスの定理を使うと
\begin{eqnarray} \frac{\mathrm{AP}}{\mathrm{PQ}} \cdot \frac{\mathrm{QB}}{\mathrm{BD}} \cdot \frac{\mathrm{DT}}{\mathrm{TA}} &=& 1 \\[5pt] \frac{2}{3} \cdot \frac{\mathrm{QB}}{\mathrm{BD}} \cdot \frac{1+3}{1} &=& 1 \\[5pt] \frac{\mathrm{QB}}{\mathrm{BD}} &=& \frac{3}{8} \\[5pt] \end{eqnarray}なので、$\mathrm{QB:BD}=3:8$ となります。

よって、 $\mathrm{BQ:QR:RD}=3:1:4$ だとわかります。

解答

ア：0 (2点)
イウ：14 (3点)
エオ：38 (2点)

解答編　つづき

問題

(2) 5点 $\mathrm{P,Q,R,S,T}$ が同一円周上にあるとし、 $\mathrm{AC}=8$ であるとする。

(i) 5点 $\mathrm{A,P,Q,S,T}$ に着目すると、 $\mathrm{AT:AS}=1:2$ より $\mathrm{AT}=\sqrt{\myBox{カ}}$ となる。さらに、5点 $\mathrm{D,Q,R,S,T}$ に着目すると $\mathrm{DR}=4\sqrt{3}$ となることがわかる。

解説

(2)
(i)
5点 $\mathrm{P,Q,R,S,T}$ が同一円周上にあるので、方べきの定理が使えます。

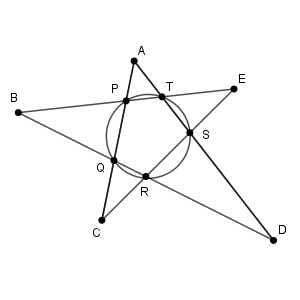
5点 $\mathrm{A,P,Q,S,T}$ に着目すると、 $\mathrm{AP\cdot AQ}=\mathrm{AT\cdot AS}$ が成り立ちます。 $\mathrm{AC}=8$ なので、 $\mathrm{AP}=2$, $\mathrm{AQ}=5$ だから、 $\mathrm{AT\cdot AS}=2\cdot5=10$ となります。また、 $\mathrm{AS}=2\mathrm{AT}$ なので、\[2\mathrm{AT}^2=10\]より $\mathrm{AT}=\sqrt{5}$ と求められます。

また、問題文にあるように、 $\mathrm{D,Q,R,S,T}$ に着目すると $\mathrm{DR\cdot DQ}=\mathrm{DS\cdot DT}$ が成り立ちます。 $\mathrm{AT}=\sqrt{5}$ なので、 $\mathrm{DS}=3\sqrt{5}$, $\mathrm{DT}=4\sqrt{5}$ だから、 $\mathrm{DR\cdot DQ}=60$ となります。(1)の最後から、 $\mathrm{DQ}=\dfrac{5}{4}\mathrm{DR}$ なので、\[\frac{5}{4}\mathrm{DR}^2=60\]より $\mathrm{DR}=4\sqrt{3}$ となることがわかります。

解答

カ：5 (3点)

解答編　つづき

問題

(ii) 3点 $\mathrm{A,B,C}$ を通る円と点 $\mathrm{D}$ との位置関係を、次の構想に基づいて調べよう。

構想
線分 $\mathrm{AC}$ と $\mathrm{BD}$ の交点 $\mathrm{Q}$ に着目し、 $\mathrm{AQ\cdot CQ}$ と $\mathrm{BQ\cdot DQ}$ の大小を比べる。

　まず、$\mathrm{AQ\cdot CQ}=5\cdot 3=15$ かつ $\mathrm{BQ\cdot DQ}=\myBox{キク}$ であるから\[ \mathrm{AQ\cdot CQ}\ \dBox{ケ}\ \mathrm{BQ\cdot DQ}\quad\cdots ① \]が成り立つ。また、3点 $\mathrm{A,B,C}$ を通る円と直線 $\mathrm{BD}$ との交点のうち、 $\mathrm{B}$ と異なる点を $\mathrm{X}$ とすると\[ \mathrm{AQ\cdot CQ}\ \dBox{コ}\ \mathrm{BQ\cdot XQ}\quad\cdots ② \]が成り立つ。①と②の左辺は同じなので、①と②の右辺を比べることにより、 $\mathrm{XQ}\ \dBox{サ}\ \mathrm{DQ}$ が得られる。したがって、点 $\mathrm{D}$ は3点 $\mathrm{A,B,C}$ を通る円の $\dBox{シ}$ にある。

　$\dbox{ケ}$ ～ $\dbox{サ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\lt$
　1: $=$
　2: $\gt$

　$\dbox{シ}$ の解答群

　0: 内部
　1: 周上
　2: 外部

解説

(ii)

$\mathrm{AQ\cdot CQ}=5\cdot 3=15$ であり、 $\mathrm{BQ\cdot DQ}=3\sqrt{3}\cdot 5\sqrt{3}=45$ なので、\[ \mathrm{AQ\cdot CQ}\lt \mathrm{BQ\cdot DQ} \]となります。

一方、 $\mathrm{X}$ について考えると、方べきの定理から\[ \mathrm{AQ\cdot CQ} = \mathrm{BQ\cdot XQ} \]となります。

この2つの式を比較すると $\mathrm{XQ}\lt \mathrm{DQ}$ なので、点 $\mathrm{D}$ は、3点 $\mathrm{A,B,C}$ を通る円の外部にあることがわかります。

問題文では $\mathrm{DQ}$ が出てきた後に $\mathrm{XQ}$ が出てきますが、後半では $\mathrm{XQ}\ \dBox{サ}\ \mathrm{DQ}$ と、 $\mathrm{XQ}$ が左辺にあるので、答えるときに不等号の向きを間違えないようにしましょう。

解答

キクケ：450 (3点)
コサシ：102 (4点)

解答編　つづき

問題

(iii) 3点 $\mathrm{C,D,E}$ を通る円と2点 $\mathrm{A,B}$ との位置関係について調べよう。

　この星型の図形において、さらに $\mathrm{CR=RS=SE}=3$ となることがわかる。したがって、点 $\mathrm{A}$ は3点 $\mathrm{C,D,E}$ を通る円の $\dBox{ス}$ にあり、点 $\mathrm{B}$ は3点 $\mathrm{C,D,E}$ を通る円の $\dBox{ス}$ にある。

　$\dbox{ス}$, $\dbox{セ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 内部
　1: 周上
　2: 外部

解説

(iii)
まずは、問題文にあることを確かめておきます。

$\triangle \mathrm{ACS}$ と直線 $\mathrm{BD}$ についてメネラウスの定理を使うと
\begin{eqnarray} \frac{\mathrm{AQ}}{\mathrm{QC}} \cdot \frac{\mathrm{CR}}{\mathrm{RS}} \cdot \frac{\mathrm{SD}}{\mathrm{DA}} &=& 1 \\[5pt] \frac{2+3}{3} \cdot \frac{\mathrm{CR}}{\mathrm{RS}} \cdot \frac{3}{3+1+1} &=& 1 \\[5pt] \frac{\mathrm{CR}}{\mathrm{RS}} &=& 1 \\[5pt] \end{eqnarray}なので、$\mathrm{CR:RS}=1:1$ となります。

また、$\triangle \mathrm{ACS}$ と直線 $\mathrm{BE}$ についてメネラウスの定理を使うと
\begin{eqnarray} \frac{\mathrm{AT}}{\mathrm{TS}} \cdot \frac{\mathrm{SE}}{\mathrm{EC}} \cdot \frac{\mathrm{CP}}{\mathrm{PA}} &=& 1 \\[5pt] \frac{1}{1} \cdot \frac{\mathrm{SE}}{\mathrm{EC}} \cdot \frac{3+3}{2} &=& 1 \\[5pt] \frac{\mathrm{SE}}{\mathrm{EC}} &=& \frac{1}{3} \\[5pt] \end{eqnarray}なので、$\mathrm{SE:EC}=1:3$ となります。

以上から、 $\mathrm{CR:RS:SE}=1:1:1$ となることがわかります。

また、 $\mathrm{C,P,Q,R,S}$ について方べきの定理から
\begin{eqnarray} \mathrm{CR} \cdot \mathrm{CS} &=& \mathrm{CQ} \cdot \mathrm{CP} \\[5pt] 2\mathrm{CR}^2 &=& 3 \cdot 6 \\[5pt] \mathrm{CR} &=& 3 \end{eqnarray}なので、たしかに $\mathrm{CR=RS=SE}=3$ となることがわかります。

$\mathrm{DS\cdot SA}=3\sqrt{5}\cdot 2\sqrt{5}=30$ であり、 $\mathrm{CS\cdot SE}=6\cdot3=18$ より大きいので、(ii)と同じように考えて、 $\mathrm{A}$ は3点 $\mathrm{C,D,E}$ を通る円の外部にあることがわかります。

$\mathrm{BR\cdot RD}=4\sqrt{3}\cdot4\sqrt{3}=48$ であり、 $\mathrm{CR\cdot RE}=3 \cdot 6=18$ より大きいので、 $\mathrm{B}$ は3点 $\mathrm{C,D,E}$ を通る円の外部にあることがわかります。

解答

スセ：22 (3点)