共通テスト数学I・数学A 2024年度第2問 [1] 解説

🕒 2024/01/14 🔄 2024/01/20

【必答問題】

問題編

問題

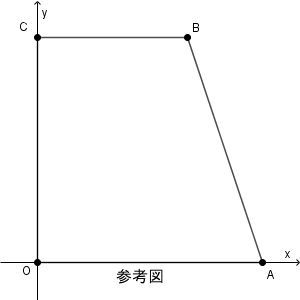
　座標平面上に4点 $\mathrm{O}(0,0)$, $\mathrm{A}(6,0)$, $\mathrm{B}(4,6)$, $\mathrm{C}(0,6)$ を頂点とする台形 $\mathrm{OABC}$ がある。また、この座標平面上で、点 $\mathrm{P, Q}$ は次の規則に従って移動する。

規則

$\mathrm{P}$ は、$\mathrm{O}$ から出発して毎秒 $1$ の一定の速さで $x$ 軸上を正の向きに $\mathrm{A}$ まで移動し、$\mathrm{A}$ に到達した時点で移動を終了する。

$\mathrm{Q}$ は、$\mathrm{C}$ から出発して $y$ 軸上を負の向きに $\mathrm{O}$ まで移動し、$\mathrm{O}$ に到達した後は $y$ 軸上を正の向きに $\mathrm{C}$ まで移動する。そして、$\mathrm{C}$ に到達した時点で移動を終了する。ただし、 $\mathrm{Q}$ は毎秒 $2$ の一定の速さで移動する。

$\mathrm{P}$, $\mathrm{Q}$ は同時刻に移動を開始する。

　この規則に従って $\mathrm{P}$, $\mathrm{Q}$ が移動するとき、$\mathrm{P}$, $\mathrm{Q}$ はそれぞれ $\mathrm{A}$, $\mathrm{C}$ に同時刻に到達し、移動を終了する。

　以下において、$\mathrm{P}$, $\mathrm{Q}$ が移動を開始する時刻を開始時刻、移動を終了する時刻を終了時刻とする。

(1) 開始時刻から $1$ 秒後の $\triangle \mathrm{PBQ}$ の面積は $\myBox{ア}$ である。

(2) 開始時刻から $3$ 秒間の $\triangle \mathrm{PBQ}$ の面積について、面積の最小値は $\myBox{イ}$ であり、最大値は $\myBox{ウエ}$ である。

(3) 開始時刻から終了時刻までの $\triangle \mathrm{PBQ}$ の面積について、面積の最小値は $\myBox{オ}$ であり、最大値は $\myBox{カキ}$ である。

(4) 開始時刻から終了時刻までの $\triangle \mathrm{PBQ}$ の面積について、面積が $10$ 以下となる時間は $\left(\myBox{ク}-\sqrt{\myBox{ケ}}+\sqrt{\myBox{コ}}\right)$ 秒間である。

考え方

式を自分で考える必要がありますが、(1)をヒントと思えば、(2)は考えやすいでしょう。(3)は3秒後からの式を考えるために、まずは Q の座標について考えるといいでしょう。(4)はまずは面積が 10 になる場合から考えてみましょう。

【必答問題】

解答編

問題

　座標平面上に4点 $\mathrm{O}(0,0)$, $\mathrm{A}(6,0)$, $\mathrm{B}(4,6)$, $\mathrm{C}(0,6)$ を頂点とする台形 $\mathrm{OABC}$ がある。また、この座標平面上で、点 $\mathrm{P, Q}$ は次の規則に従って移動する。

規則

$\mathrm{P}$ は、$\mathrm{O}$ から出発して毎秒 $1$ の一定の速さで $x$ 軸上を正の向きに $\mathrm{A}$ まで移動し、$\mathrm{A}$ に到達した時点で移動を終了する。

$\mathrm{Q}$ は、$\mathrm{C}$ から出発して $y$ 軸上を負の向きに $\mathrm{O}$ まで移動し、$\mathrm{O}$ に到達した後は $y$ 軸上を正の向きに $\mathrm{C}$ まで移動する。そして、$\mathrm{C}$ に到達した時点で移動を終了する。ただし、 $\mathrm{Q}$ は毎秒 $2$ の一定の速さで移動する。

$\mathrm{P}$, $\mathrm{Q}$ は同時刻に移動を開始する。

　この規則に従って $\mathrm{P}$, $\mathrm{Q}$ が移動するとき、$\mathrm{P}$, $\mathrm{Q}$ はそれぞれ $\mathrm{A}$, $\mathrm{C}$ に同時刻に到達し、移動を終了する。

　以下において、$\mathrm{P}$, $\mathrm{Q}$ が移動を開始する時刻を開始時刻、移動を終了する時刻を終了時刻とする。

(1) 開始時刻から $1$ 秒後の $\triangle \mathrm{PBQ}$ の面積は $\myBox{ア}$ である。

解説

(1)

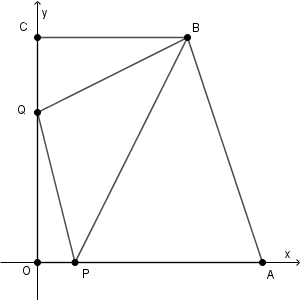
$\mathrm{P}(1,0)$, $\mathrm{Q}(0,4)$ なので、$\triangle \mathrm{ABP}$ の面積は $\dfrac{5\cdot 6}{2}=15$ 、$\triangle \mathrm{BCQ}$ の面積は $\dfrac{2\cdot 4}{2}=4$ 、$\triangle \mathrm{OPQ}$ の面積は $\dfrac{1\cdot 4}{2}=2$ です。また、台形の面積は\[ \frac{(4+6)\cdot 6}{2}=30 \]なので、 $\triangle \mathrm{PBQ}$ の面積は\[ 30-15-4-2=9 \]となります。

解答

ア：9 (3点)

解答編　つづき

問題

(2) 開始時刻から $3$ 秒間の $\triangle \mathrm{PBQ}$ の面積について、面積の最小値は $\myBox{イ}$ であり、最大値は $\myBox{ウエ}$ である。

解説

(2)
$0\leqq x\leqq 3$ のとき、 $x$ 秒後における $\triangle \mathrm{PBQ}$ の面積を考えます。

$\mathrm{P}(x,0)$, $\mathrm{Q}(0,6-2x)$ なので、$\triangle \mathrm{ABP}$ の面積は $\dfrac{(6-x)\cdot 6}{2}=3(6-x)$ 、$\triangle \mathrm{BCQ}$ の面積は $\dfrac{2x\cdot 4}{2}=4x$ 、$\triangle \mathrm{OPQ}$ の面積は $\dfrac{x\cdot (6-2x)}{2}=x(3-x)$ です。また、台形の面積は $30$ なので、 $\triangle \mathrm{PBQ}$ の面積は
\begin{eqnarray} & & 30 -3(6-x)-4x-x(3-x) \\[5pt] &=& 30 -18+3x-4x+x^2-3x \\[5pt] &=& x^2-4x+12 \\[5pt] &=& (x-2)^2+8 \\[5pt] \end{eqnarray}となります。

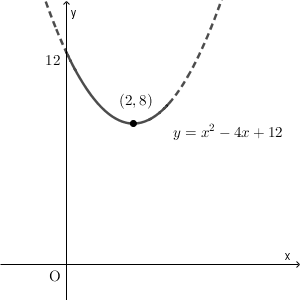
よって、 $x=2$ のとき最小値 $8$ をとり、 $x=0$ のとき最大値 $12$ をとることがわかります。

解答

イ：8 (3点)
ウエ：12 (2点)

解答編　つづき

問題

(3) 開始時刻から終了時刻までの $\triangle \mathrm{PBQ}$ の面積について、面積の最小値は $\myBox{オ}$ であり、最大値は $\myBox{カキ}$ である。

解説

(3)
$3\leqq x\leqq 6$ のとき、 $x$ 秒後における $\triangle \mathrm{PBQ}$ の面積を考えます。

$\mathrm{P}(x,0)$, $\mathrm{Q}(0,2x-6)$ なので、$\triangle \mathrm{ABP}$ の面積は $3(6-x)$ 、$\triangle \mathrm{BCQ}$ の面積は $\dfrac{(12-2x)\cdot 4}{2}=2(12-2x)$ 、$\triangle \mathrm{OPQ}$ の面積は $\dfrac{x\cdot (2x-6)}{2}=x(x-3)$ です。また、台形の面積は $30$ なので、 $\triangle \mathrm{PBQ}$ の面積は
\begin{eqnarray} & & 30 -3(6-x)-2(12-2x)-x(x-3) \\[5pt] &=& 30 -18+3x -24+4x -x^2+3x \\[5pt] &=& -x^2 +10x -12 \\[5pt] &=& -(x-5)^2+13 \\[5pt] \end{eqnarray}となります。

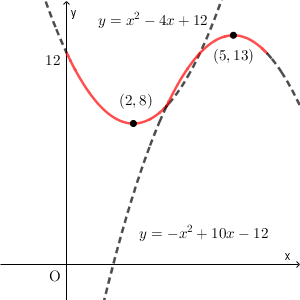
よって、全体では、 $x=2$ のときに最小値 $8$ をとり、 $x=5$ のときに最大値 $13$ をとることがわかります。

解答

オ：8 (1点)
カキ：13 (2点)

解答編　つづき

問題

(4) 開始時刻から終了時刻までの $\triangle \mathrm{PBQ}$ の面積について、面積が $10$ 以下となる時間は $\left(\myBox{ク}-\sqrt{\myBox{ケ}}+\sqrt{\myBox{コ}}\right)$ 秒間である。

解説

(4)

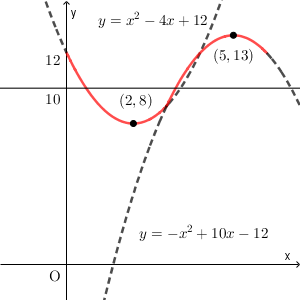
まずは、 $0\leqq x\leqq 3$ の場合を考えます。

$x^2-4x+12=10$ を解くと
\begin{eqnarray} x^2-4x+12 &=& 10 \\[5pt] x^2-4x+2 &=& 0 \\[5pt] x &=& 2\pm\sqrt{4-2} \\[5pt] &=& 2\pm\sqrt{2} \end{eqnarray}となります。なので、 $0\leqq x\leqq 3$ の範囲で、面積が $10$ 以下となるのは、 $2-\sqrt{2}\leqq x\leqq 3$ のときだとわかります。

次に、 $3\leqq x\leqq 6$ の場合を考えます。 $-x^2 +10x -12=10$ を解くと
\begin{eqnarray} -x^2 +10x -12 &=& 10 \\[5pt] x^2-10x+22 &=& 0 \\[5pt] x &=& 5\pm\sqrt{25-22} \\[5pt] &=& 5\pm\sqrt{3} \end{eqnarray}となります。なので、 $3\leqq x\leqq 6$ の範囲で、面積が $10$ 以下となるのは、 $3\leqq x\leqq 5-\sqrt{3}$ のときだとわかります。

以上から、面積が $10$ 以下となるのは $2-\sqrt{2} \leqq x \leqq 5-\sqrt{3}$ のときだとわかるので、この間の時間は
\begin{eqnarray} (5-\sqrt{3})-(2-\sqrt{2}) &=& 3-\sqrt{3}+\sqrt{2} \end{eqnarray}秒間と求められます。