共通テスト 数学I・数学A 2024年度 第2問 [2] 解説

【必答問題】

問題編

問題

　高校の陸上部で長距離競技の選手として活躍する太郎さんは、長距離競技の公認記録が掲載されているWebページを見つけた。このWebページでは、各選手における公認記録のうち最も速いものが掲載されている。そのWebページに掲載されている、ある選手のある長距離競技での公認記録を、その選手のその競技でのベストタイムということにする。

　なお、以下の図や表については、ベースボール・マガジン社「陸上競技ランキング」のWebページをもとに作成している。

(1) 太郎さんは、男子マラソンの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA、データBとした。

　ここでは、マラソンのベストタイムは、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。例えば2時間5分30秒であれば、 $60\times5+30=330$(秒)となる。

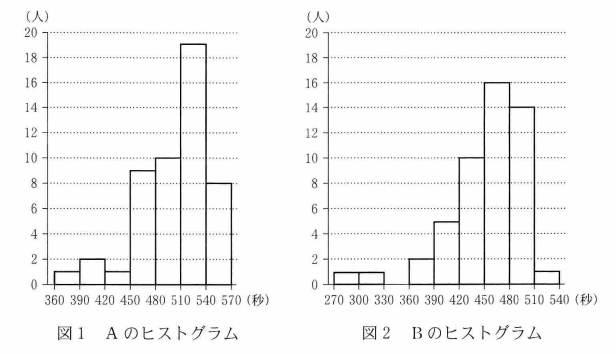
(i) 図1と図2はそれぞれ、階級の幅を30秒としたAとBのヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　図1からAの最頻値は階級 $\dBox{サ}$ の階級値である。また、図2からBの中央値が含まれる階級は $\dBox{シ}$ である。

　$\dbox{サ}$, $\dbox{シ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 270以上 300未満
　1: 300以上 330未満
　2: 330以上 360未満
　3: 360以上 390未満
　4: 390以上 420未満
　5: 420以上 450未満
　6: 450以上 480未満
　7: 480以上 510未満
　8: 510以上 540未満
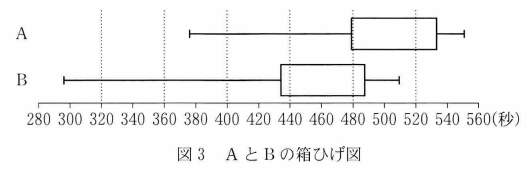
　9: 540以上 570未満

(ii) 図3は、A, B それぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。

　図3より次のことが読み取れる。ただし、A, B それぞれにおける、速い方から13番目の選手は、一人ずつとする。

• Bの速い方から13番目の選手のベストタイムは、Aの速い方から13番目の選手のベストタイムより、およそ $\dBox{ス}$ 秒速い。
• Aの四分位範囲から Bの四分位範囲を引いた差の絶対値は $\dBox{セ}$ である。

　$\dbox{ス}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つ選べ。

　0: 5
　1: 15
　2: 25
　3: 35
　4: 45
　5: 55

　$\dbox{セ}$ の解答群

　0: 0以上 20未満
　1: 20以上 40未満
　2: 40以上 60未満
　3: 60以上 80未満
　4: 80以上 100未満

(iii) 太郎さんは、Aのある選手とBのある選手のベストタイムの比較において、その二人の選手のベストタイムが速いか遅いかとは別の観点でも考えるために、次の式を満たす $z$ の値を用いて判断することにした。

式
（あるデータのある選手のベストタイム）＝
　　（そのデータの平均値）＋$z$ ×（そのデータの標準偏差）

　二人の選手それぞれのベストタイムに対する $z$ の値を比較し、その値の小さい選手の方が優れていると判断する。

　表1は、A, B それぞれにおける、速い方から1番目の選手（以下、1位の選手）のベストタイムと、データの平均値と標準偏差をまとめたものである。

表1　1位の選手のベストタイム、平均値、標準偏差

データ	1位の選手のベストタイム	平均値	標準偏差
A	$376$	$504$	$40$
B	$296$	$454$	$45$

　式と表1を用いると、Bの1位の選手のベストタイムに対する $z$ の値は\[ z=-\myBox{ソ}.\ \myBox{タチ} \]である。このことから、Bの1位の選手のベストタイムは、平均値より標準偏差のおよそ $\mybox{ソ}.\ \mybox{タチ}$ 倍だけ小さいことがわかる。

　A, B それぞれにおける、1位の選手についての記述として、次の 0 ～ 3 のうち、正しいものは $\dBox{ツ}$ である。

　$\dbox{ツ}$ の解答群

　0: ベストタイムで比較するとAの1位の選手の方が速く、 $z$ の値で比較するとAの1位の選手の方が優れている。

　1: ベストタイムで比較するとBの1位の選手の方が速く、 $z$ の値で比較するとBの1位の選手の方が優れている。

　2: ベストタイムで比較するとAの1位の選手の方が速く、 $z$ の値で比較するとBの1位の選手の方が優れている。

　3: ベストタイムで比較するとBの1位の選手の方が速く、 $z$ の値で比較するとAの1位の選手の方が優れている。

(2) 太郎さんは、マラソン、10000m、5000m のベストタイムに関連がないかを調べることにした。そのために、2022年末時点のこれら3種目のベストタイムをすべて確認できた日本人男子選手のうち、マラソンのベストタイムが速い方から50人を選んだ。

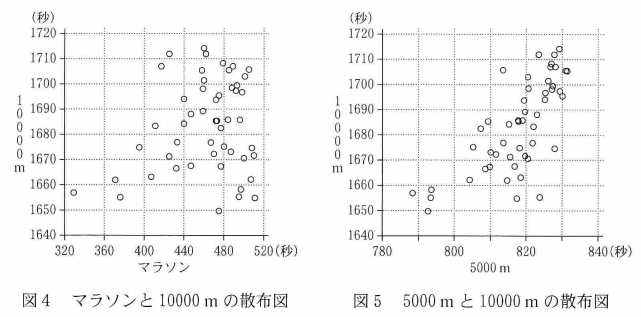
　図4と図5はそれぞれ、選んだ50人についてのマラソンと 10000m のベストタイム、5000m と 10000m のベストタイムの散布図である。ただし、5000m と 10000m のベストタイムは秒単位で表し、マラソンのベストタイムは(1)の場合と同様、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。なお、これらの散布図には、完全に重なっている点はない。

　次の (a), (b) は、図4と図5に関する記述である。

(a) マラソンのベストタイムの速い方から3番目までの選手の 10000m のベストタイムは、3選手とも 1670秒未満である。

(b) マラソンと 10000m の間の相関は、5000m と 10000m の間の相関より強い。

　(a), (b) の正誤の組合せとして正しいものは $\dBox{テ}$ である。

　$\dbox{テ}$ の解答群

　0: (a)正　(b)正
　1: (a)正　(b)誤
　2: (a)誤　(b)正
　3: (a)誤　(b)誤

考え方

ヒストグラムや箱ひげ図、散布図を読み解く問題は、標準的な問題です。(1)(iii)で、独自の評価方法について考える問題がありますが、式に当てはめて考えるだけです。

【必答問題】

解答編

問題

　高校の陸上部で長距離競技の選手として活躍する太郎さんは、長距離競技の公認記録が掲載されているWebページを見つけた。このWebページでは、各選手における公認記録のうち最も速いものが掲載されている。そのWebページに掲載されている、ある選手のある長距離競技での公認記録を、その選手のその競技でのベストタイムということにする。

　なお、以下の図や表については、ベースボール・マガジン社「陸上競技ランキング」のWebページをもとに作成している。

(1) 太郎さんは、男子マラソンの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA、データBとした。

　ここでは、マラソンのベストタイムは、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。例えば2時間5分30秒であれば、 $60\times5+30=330$(秒)となる。

(i) 図1と図2はそれぞれ、階級の幅を30秒としたAとBのヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　図1からAの最頻値は階級 $\dBox{サ}$ の階級値である。また、図2からBの中央値が含まれる階級は $\dBox{シ}$ である。

　$\dbox{サ}$, $\dbox{シ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 270以上 300未満
　1: 300以上 330未満
　2: 330以上 360未満
　3: 360以上 390未満
　4: 390以上 420未満
　5: 420以上 450未満
　6: 450以上 480未満
　7: 480以上 510未満
　8: 510以上 540未満
　9: 540以上 570未満

解説

(1)
(i)
Aの最頻値とは、一番棒が長いところを見ればいいので、510以上540未満の階級の階級値となります。

全体で50個の値があるので、Bの中央値は、25番目と26番目の値を平均したものです。どちらも450以上480未満の階級にあるので、Bの中央値もこの階級に含まれます。

解答

サ：8 (2点)
シ：6 (2点)

解答編　つづき

問題

(ii) 図3は、A, B それぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。

　図3より次のことが読み取れる。ただし、A, B それぞれにおける、速い方から13番目の選手は、一人ずつとする。

• Bの速い方から13番目の選手のベストタイムは、Aの速い方から13番目の選手のベストタイムより、およそ $\dBox{ス}$ 秒速い。
• Aの四分位範囲から Bの四分位範囲を引いた差の絶対値は $\dBox{セ}$ である。

　$\dbox{ス}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つ選べ。

　0: 5
　1: 15
　2: 25
　3: 35
　4: 45
　5: 55

　$\dbox{セ}$ の解答群

　0: 0以上 20未満
　1: 20以上 40未満
　2: 40以上 60未満
　3: 60以上 80未満
　4: 80以上 100未満

解説

(ii)
全体で50人いるので、第1四分位数は、速い方から13番目のタイムとなります。Bの第1四分位数はだいたい435で、Aの第一四分位数はだいたい480なので、Bのほうがおよそ45秒速いことがわかります。

Aの四分位範囲は、およそ 530-480=50 秒です。Bの四分位範囲は、およそ 485-435=50 秒なので、差の絶対値は 0以上20未満です。

解答

ス：4 (2点)
セ：0 (2点)

解答編　つづき

問題

(iii) 太郎さんは、Aのある選手とBのある選手のベストタイムの比較において、その二人の選手のベストタイムが速いか遅いかとは別の観点でも考えるために、次の式を満たす $z$ の値を用いて判断することにした。

式
（あるデータのある選手のベストタイム）＝
　　（そのデータの平均値）＋$z$ ×（そのデータの標準偏差）

　二人の選手それぞれのベストタイムに対する $z$ の値を比較し、その値の小さい選手の方が優れていると判断する。

　表1は、A, B それぞれにおける、速い方から1番目の選手（以下、1位の選手）のベストタイムと、データの平均値と標準偏差をまとめたものである。

表1　1位の選手のベストタイム、平均値、標準偏差

データ	1位の選手のベストタイム	平均値	標準偏差
A	$376$	$504$	$40$
B	$296$	$454$	$45$

　式と表1を用いると、Bの1位の選手のベストタイムに対する $z$ の値は\[ z=-\myBox{ソ}.\ \myBox{タチ} \]である。このことから、Bの1位の選手のベストタイムは、平均値より標準偏差のおよそ $\mybox{ソ}.\ \mybox{タチ}$ 倍だけ小さいことがわかる。

　A, B それぞれにおける、1位の選手についての記述として、次の 0 ～ 3 のうち、正しいものは $\dBox{ツ}$ である。

　$\dbox{ツ}$ の解答群

　0: ベストタイムで比較するとAの1位の選手の方が速く、 $z$ の値で比較するとAの1位の選手の方が優れている。

　1: ベストタイムで比較するとBの1位の選手の方が速く、 $z$ の値で比較するとBの1位の選手の方が優れている。

　2: ベストタイムで比較するとAの1位の選手の方が速く、 $z$ の値で比較するとBの1位の選手の方が優れている。

　3: ベストタイムで比較するとBの1位の選手の方が速く、 $z$ の値で比較するとAの1位の選手の方が優れている。

解説

(iii)
Bについて、1位の選手のベストタイムは296、平均値は454、標準偏差は45なので、問題文にある $z$ を求めると
\begin{eqnarray} & & 296=454+z\cdot 45 \\[5pt] & & 45z=-158 \\[5pt] & & z=-3.511\cdots \\[5pt] \end{eqnarray}となります。

また、Aについても同様に求めると
\begin{eqnarray} & & 376 = 504+40z \\[5pt] & & 40z = -128 \\[5pt] & & z = -3.2 \\[5pt] \end{eqnarray}となります。

1位の選手のベストタイムは、A：376 と B：296 なので、Bのほうがはやいです。

また、$z$ の値だと、Aは $-3.2$ で Bは $-3.511\cdots$ なので、Bのほうが小さいから、Bのほうが優れているといえます。

問題文では、Bについて聞かれた後に、AとBの比較をするという流れです。Aから聞かれているわけではないので、前半でAについて答えてしまったり、後半でAとBの値を反対にして答えてしまったりといった間違いがないようにしましょう。

解答

ソタチ：351 (2点)
ツ：1 (2点)

解答編　つづき

問題

(2) 太郎さんは、マラソン、10000m、5000m のベストタイムに関連がないかを調べることにした。そのために、2022年末時点のこれら3種目のベストタイムをすべて確認できた日本人男子選手のうち、マラソンのベストタイムが速い方から50人を選んだ。

　図4と図5はそれぞれ、選んだ50人についてのマラソンと 10000m のベストタイム、5000m と 10000m のベストタイムの散布図である。ただし、5000m と 10000m のベストタイムは秒単位で表し、マラソンのベストタイムは(1)の場合と同様、実際のベストタイムから2時間を引いた時間を秒単位で表したものとする。なお、これらの散布図には、完全に重なっている点はない。

　次の (a), (b) は、図4と図5に関する記述である。

(a) マラソンのベストタイムの速い方から3番目までの選手の 10000m のベストタイムは、3選手とも 1670秒未満である。

(b) マラソンと 10000m の間の相関は、5000m と 10000m の間の相関より強い。

　(a), (b) の正誤の組合せとして正しいものは $\dBox{テ}$ である。

　$\dbox{テ}$ の解答群

　0: (a)正　(b)正
　1: (a)正　(b)誤
　2: (a)誤　(b)正
　3: (a)誤　(b)誤

解説

(2)
それぞれの選択肢を考えます。

図4を見ます。マラソンのベストタイムのはやい方から3番目までとは、左にある点を見ればいいです。それら3つの点は、縦に見ると、1670未満なので、10000mのベストタイムは3選手とも1670秒未満といえます。なので、(a)は正しいです。

図4と図5では、右のほうが強い相関があると言えるので、(b)は誤りです。

解答

テ：1 (3点)