共通テスト 数学I・数学A 2024年度 第1問 [2] 解説

【必答問題】

問題編

問題

（三角比の表は省略しています）

　以下の問題を解答するにあたっては、必要に応じて37ページの三角比の表を用いてもよい。

　水平な地面（以下、地面）に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。

　図1のように、電柱の影の先端は坂の斜面（以下、坂）にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには 7% と表示されているとする。

　電柱の太さと影の幅は無視して考えるものとする。また、地面と坂は平面であるとし、地面と坂が交わってできる直線を $\ell$ とする。

　電柱の先端を点 $\mathrm{A}$ とし、根もとを点 $\mathrm{B}$ とする。電柱の影について、地面にある部分を線分 $\mathrm{BC}$ とし、坂にある部分を線分 $\mathrm{CD}$ とする。線分 $\mathrm{BC, CD}$ がそれぞれ $\ell$ と垂直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。

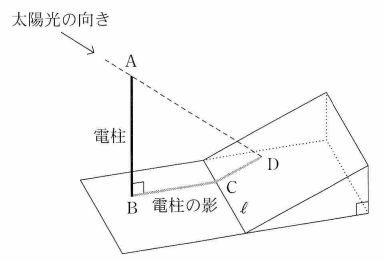
　電柱の影が坂に向かってまっすぐにのびているとする。このとき、4点 $\mathrm{A, B ,C, D}$ を通る平面は $\ell$ と垂直である。その平面において、図2のように、直線 $\mathrm{AD}$ と直線 $\mathrm{BC}$ の交点を $\mathrm{P}$ とすると、太陽高度とは $\angle \mathrm{APB}$ の大きさのことである。

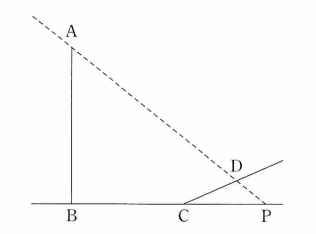
　道路標識の 7% という表示は、この坂をのぼったとき、$100\mathrm{m}$ の水平距離に対して $7\mathrm{m}$ の割合で高くなることを示している。 $n$ を $1$ 以上 $9$ 以下の整数とするとき、坂の傾斜角 $\angle \mathrm{DCP}$ の大きさについて\[ n^{\circ} \lt \angle \mathrm{DCP} \lt n^{\circ}+1^{\circ} \]を満たす $n$ の値は $\myBox{シ}$ である。

　以下では、 $\angle \mathrm{DCP}$ の大きさは、ちょうど $\mybox{シ}^{\circ}$ であるとする。

　ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところ $\mathrm{BC}=7\mathrm{m}$、$\mathrm{CD}=4\mathrm{m}$ であり、太陽高度は $\angle \mathrm{APB}=45^{\circ}$ であった。点 $\mathrm{D}$ から直線 $\mathrm{AB}$ に垂直な直線を引き、直線 $\mathrm{AB}$ との交点を $\mathrm{E}$ とするとき\[ \mathrm{BE}=\myBox{ス}\times\dBox{セ} \mathrm{m} \]であり、\[ \mathrm{DE}=\left(\myBox{ソ}+\myBox{タ}\times\dBox{チ}\right) \mathrm{m} \]である。よって、電柱の高さは、小数第2位で四捨五入すると $\dBox{ツ}\mathrm{m}$ であることがわかる。

　$\dbox{セ}, \dbox{チ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\sin\angle \mathrm{DCP}$

　1: $\dfrac{1}{\sin\angle \mathrm{DCP}}$

　2: $\cos\angle \mathrm{DCP}$

　3: $\dfrac{1}{\cos\angle \mathrm{DCP}}$

　4: $\tan\angle \mathrm{DCP}$

　5: $\dfrac{1}{\tan\angle \mathrm{DCP}}$

　$\dbox{ツ}$ の解答群

　0: $10.4$
　1: $10.7$
　2: $11.0$
　3: $11.3$
　4: $11.6$
　5: $11.9$

　別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は $\angle \mathrm{APB}=42^{\circ}$ であった。電柱の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある部分の長さは\[ \mathrm{CD}=\dfrac{\mathrm{AB}-\myBox{テ}\times\dBox{ト}}{\dBox{ナ}+\dBox{ニ}\times\dbox{ト}} \mathrm{m} \]である。 $\mathrm{AB}=\dbox{ツ}\mathrm{m}$ として、これを計算することにより、この日の電柱の影について、坂にある部分の長さは、前回調べた $4\mathrm{m}$ より約 $1.2\mathrm{m}$ だけ長いことがわかる。

　$\dbox{ト}$ ～ $\dbox{ニ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\sin\angle \mathrm{DCP}$
　1: $\cos\angle \mathrm{DCP}$
　2: $\tan\angle \mathrm{DCP}$
　3: $\sin\angle 42^{\circ}$
　4: $\cos\angle 42^{\circ}$
　5: $\tan\angle 42^{\circ}$

考え方

太陽や坂の絵がありますが、図形の問題と思って考えていけばいいです。後半は、使える角と長さに注意して、CD を含む式を作り、CD について解くのですが、結構計算が大変です。計算力が必要です。

【必答問題】

解答編

問題

（三角比の表は省略しています）

　以下の問題を解答するにあたっては、必要に応じて37ページの三角比の表を用いてもよい。

　水平な地面（以下、地面）に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。

　図1のように、電柱の影の先端は坂の斜面（以下、坂）にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには 7% と表示されているとする。

　電柱の太さと影の幅は無視して考えるものとする。また、地面と坂は平面であるとし、地面と坂が交わってできる直線を $\ell$ とする。

　電柱の先端を点 $\mathrm{A}$ とし、根もとを点 $\mathrm{B}$ とする。電柱の影について、地面にある部分を線分 $\mathrm{BC}$ とし、坂にある部分を線分 $\mathrm{CD}$ とする。線分 $\mathrm{BC, CD}$ がそれぞれ $\ell$ と垂直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。

　電柱の影が坂に向かってまっすぐにのびているとする。このとき、4点 $\mathrm{A, B ,C, D}$ を通る平面は $\ell$ と垂直である。その平面において、図2のように、直線 $\mathrm{AD}$ と直線 $\mathrm{BC}$ の交点を $\mathrm{P}$ とすると、太陽高度とは $\angle \mathrm{APB}$ の大きさのことである。

　道路標識の 7% という表示は、この坂をのぼったとき、$100\mathrm{m}$ の水平距離に対して $7\mathrm{m}$ の割合で高くなることを示している。 $n$ を $1$ 以上 $9$ 以下の整数とするとき、坂の傾斜角 $\angle \mathrm{DCP}$ の大きさについて\[ n^{\circ} \lt \angle \mathrm{DCP} \lt n^{\circ}+1^{\circ} \]を満たす $n$ の値は $\myBox{シ}$ である。

　以下では、 $\angle \mathrm{DCP}$ の大きさは、ちょうど $\mybox{シ}^{\circ}$ であるとする。

解説

$\tan\angle \mathrm{DCP}=0.07$ なので、 $\tan4^{\circ}=0.0699$ と $\tan5^{\circ}=0.0875$ の間にあるから\[ 4^{\circ} \lt \angle\mathrm{DCP} \lt 5^{\circ} \]です。

解答

シ：4 (4点)

解答編　つづき

問題

　ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところ $\mathrm{BC}=7\mathrm{m}$、$\mathrm{CD}=4\mathrm{m}$ であり、太陽高度は $\angle \mathrm{APB}=45^{\circ}$ であった。点 $\mathrm{D}$ から直線 $\mathrm{AB}$ に垂直な直線を引き、直線 $\mathrm{AB}$ との交点を $\mathrm{E}$ とするとき\[ \mathrm{BE}=\myBox{ス}\times\dBox{セ} \mathrm{m} \]であり、\[ \mathrm{DE}=\left(\myBox{ソ}+\myBox{タ}\times\dBox{チ}\right) \mathrm{m} \]である。よって、電柱の高さは、小数第2位で四捨五入すると $\dBox{ツ}\mathrm{m}$ であることがわかる。

　$\dbox{セ}, \dbox{チ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\sin\angle \mathrm{DCP}$

　1: $\dfrac{1}{\sin\angle \mathrm{DCP}}$

　2: $\cos\angle \mathrm{DCP}$

　3: $\dfrac{1}{\cos\angle \mathrm{DCP}}$

　4: $\tan\angle \mathrm{DCP}$

　5: $\dfrac{1}{\tan\angle \mathrm{DCP}}$

　$\dbox{ツ}$ の解答群

　0: $10.4$
　1: $10.7$
　2: $11.0$
　3: $11.3$
　4: $11.6$
　5: $11.9$

解説

$\mathrm{BE}$ は $\mathrm{CD} \sin\angle\mathrm{DCP}$ と一致するので、 $\mathrm{BE}=4\sin\angle\mathrm{DCP}$ です。

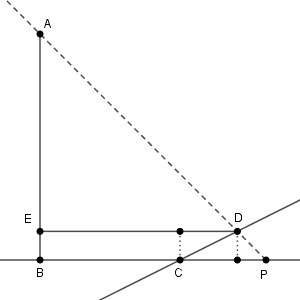
また、$\mathrm{DE}$ は $\mathrm{BC}+\mathrm{CD} \cos\angle\mathrm{DCP}$ と一致するので、 $\mathrm{DE}=7+4\cos\angle\mathrm{DCP}$ です。

太陽高度が $45^{\circ}$ なので、 $\mathrm{AE=DE}$ だから、電柱の高さは $\mathrm{BE+DE}$ となります。
\begin{eqnarray} & & 4\sin\angle\mathrm{DCP} +7+4\cos\angle\mathrm{DCP} \\[5pt] &=& 4\sin 4^{\circ} +7+4\cos4^{\circ} \\[5pt] &=& 4 \cdot 0.0698 +7+4 \cdot 0.9976 \\[5pt] &=& 11.26 \end{eqnarray}となるので、小数第2位を四捨五入して $11.3$ となります。

解答

スセ：40 (4点)
ソタチ：742 (4点)
ツ：3 (4点)

解答編　つづき

問題

　別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は $\angle \mathrm{APB}=42^{\circ}$ であった。電柱の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある部分の長さは\[ \mathrm{CD}=\dfrac{\mathrm{AB}-\myBox{テ}\times\dBox{ト}}{\dBox{ナ}+\dBox{ニ}\times\dbox{ト}} \mathrm{m} \]である。 $\mathrm{AB}=\dbox{ツ}\mathrm{m}$ として、これを計算することにより、この日の電柱の影について、坂にある部分の長さは、前回調べた $4\mathrm{m}$ より約 $1.2\mathrm{m}$ だけ長いことがわかる。

　$\dbox{ト}$ ～ $\dbox{ニ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $\sin\angle \mathrm{DCP}$
　1: $\cos\angle \mathrm{DCP}$
　2: $\tan\angle \mathrm{DCP}$
　3: $\sin\angle 42^{\circ}$
　4: $\cos\angle 42^{\circ}$
　5: $\tan\angle 42^{\circ}$

解説

$\mathrm{AB}$ は $\mathrm{AE+EB}$ とかけます。これはいつでも成り立ちます。

太陽高度が $42^{\circ}$ なので、 $\tan 42^{\circ}=\dfrac{\mathrm{AE}}{\mathrm{DE}}$ だから $\mathrm{AE}=\mathrm{DE}\tan 42^{\circ}$ となります。さらに、 $\mathrm{DE}=\mathrm{BC}+\mathrm{CD} \cos\angle\mathrm{DCP}$ であり、 $\mathrm{BC}=7$ も変わらないので、\[ \mathrm{AE}=(7+\mathrm{CD} \cos\angle\mathrm{DCP})\tan 42^{\circ} \]が成り立ちます。

また、$\mathrm{EB}=\mathrm{CD}\sin\angle\mathrm{DCP}$ が成り立ちます。

これらから
\begin{eqnarray} \mathrm{AB} &=& \mathrm{AE+EB} \\[5pt] \mathrm{AB} &=& (7+\mathrm{CD} \cos\angle\mathrm{DCP})\tan 42^{\circ} + \mathrm{CD}\sin\angle\mathrm{DCP} \\[5pt] \mathrm{AB} &=& 7\tan 42^{\circ}+\mathrm{CD} \cos\angle\mathrm{DCP}\tan 42^{\circ} + \mathrm{CD}\sin\angle\mathrm{DCP} \\[5pt] \mathrm{AB}-7\tan 42^{\circ} &=& \mathrm{CD} (\cos\angle\mathrm{DCP}\tan 42^{\circ}+\sin\angle\mathrm{DCP}) \\[5pt] \mathrm{CD} &=& \frac{\mathrm{AB}-7\tan 42^{\circ}} {\sin\angle\mathrm{DCP}+\cos\angle\mathrm{DCP}\tan 42^{\circ}} \\[5pt] \end{eqnarray}と求められます。実際に代入して計算すると、 $5.16\cdots$ となり、たしかに、 $4$ より約 $1.2$ だけ大きな値になることがわかります。

解答

テトナニ：7501 (4点)