共通テスト 数学I・数学A 2022年度追試 第5問 解説
【第3問~第5問から2問選択】
問題編
問題
(1) 円と直線に関する次の定理を考える。
定理
3点 P, Q, R は一直線上にこの順に並んでいるとし、点 T はこの直線上にないものとする。このとき、 $\mathrm{ PQ }\cdot \mathrm{ PR }=\mathrm{ PT }^2$ が成り立つならば、直線 PT は3点 Q, R, T を通る円に接する。この定理が成り立つことは、次のように説明できる。
直線 PT は3点 Q, R, T を通る円 O に接しないとする。このとき、直線 PT は円 O と異なる2点で交わる。直線 PT と円 O との交点で点 T とは異なる点を $\mathrm{ T' }$ とすると\[
\mathrm{ PT }\cdot \mathrm{ PT' } =\dBox{ア}\cdot\dBox{イ} \]が成り立つ。点 $\mathrm{ T }$ と点 $\mathrm{ T' }$ が異なることにより、 $\mathrm{ PT }\cdot \mathrm{ PT' }$ の値と $\mathrm{ PT }^2$ の値は異なる。したがって、 $\mathrm{ PQ }\cdot \mathrm{ PR }=\mathrm{ PT }^2$ に矛盾するので、背理法により、直線 PT は3点 Q, R, T を通る円に接するといえる。$\dbox{ア}, \dbox{イ}$ の解答群(解答の順序は問わない。)
0: PQ
1: PR
2: QR
3: QT
4: RT(2) $\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=\dfrac{1}{2}$, $\mathrm{ BC }=\dfrac{3}{4}$, $\mathrm{ AC }=1$ とする。
このとき、 $\angle \mathrm{ ABC }$ の二等分線と辺 AC との交点を D とすると、 $\mathrm{ AD }=\dfrac{\myBox{ウ} }{\myBox{エ} }$ である。直線 BC 上に、点 C とは異なり、 $\mathrm{ BC }=\mathrm{ BE }$ となる点 E をとる。 $\angle \mathrm{ ABE }$ の二等分線と線分 AE との交点を F とし、直線 AC との交点を G とすると
\begin{eqnarray} \dfrac{\mathrm{ AC } }{\mathrm{ AG } } &=& \dfrac{\myBox{オ} }{\myBox{カ} } \ , \\[5pt] \dfrac{\triangle\mathrm{ ABF }\ \sf{の面積}}{\triangle\mathrm{ AFG }\ \sf{の面積}} &=& \dfrac{\myBox{キ} }{\myBox{ク} } \\[5pt] \end{eqnarray}である。線分 DG の中点を H とすると、 $\mathrm{ BH }=\dfrac{\myBox{ケ} }{\myBox{コ} }$ である。また\[ \mathrm{ AH }=\dfrac{\myBox{サ} }{\myBox{シ} }, \ \mathrm{ CH }=\dfrac{\myBox{ス} }{\myBox{セ} } \]である。
$\triangle \mathrm{ ABC }$ の外心を O とする。 $\triangle \mathrm{ ABC }$ の外接円 O の半径が $\dfrac{\myBox{ソ}\sqrt{\myBox{タチ} }}{\myBox{ツテ} }$ であることから、線分 BH を $1:2$ に内分する点を I とすると\[ \mathrm{ IO }=\dfrac{\myBox{ト}\sqrt{\myBox{ナ} }}{\myBox{ニヌ} } \]であることがわかる。
考え方
(1)で抽象的なケース、(2)で具体的なケースを扱います。このつながりが少しわかりづらいかもしれません。
また、(2)の中盤のケコは、唐突感があり、何を使って求めるのかがわかりづらいです。その後のサ~セのほうが考えやすいでしょう。
ソ~テも唐突感があり、最後のト~ヌもどう求めればいいのか気づきにくいかもしれません。
教科書にある基本的な定理を知っているだけでなく、使いこなせるようにしておく必要があり、また、文脈を読んで行間を埋めて解く力も必要で、なかなか難しい問題です。
【第3問~第5問から2問選択】
解答編
問題
(1) 円と直線に関する次の定理を考える。
定理
3点 P, Q, R は一直線上にこの順に並んでいるとし、点 T はこの直線上にないものとする。このとき、 $\mathrm{ PQ }\cdot \mathrm{ PR }=\mathrm{ PT }^2$ が成り立つならば、直線 PT は3点 Q, R, T を通る円に接する。この定理が成り立つことは、次のように説明できる。
直線 PT は3点 Q, R, T を通る円 O に接しないとする。このとき、直線 PT は円 O と異なる2点で交わる。直線 PT と円 O との交点で点 T とは異なる点を $\mathrm{ T' }$ とすると\[
\mathrm{ PT }\cdot \mathrm{ PT' } =\dBox{ア}\cdot\dBox{イ} \]が成り立つ。点 $\mathrm{ T }$ と点 $\mathrm{ T' }$ が異なることにより、 $\mathrm{ PT }\cdot \mathrm{ PT' }$ の値と $\mathrm{ PT }^2$ の値は異なる。したがって、 $\mathrm{ PQ }\cdot \mathrm{ PR }=\mathrm{ PT }^2$ に矛盾するので、背理法により、直線 PT は3点 Q, R, T を通る円に接するといえる。$\dbox{ア}, \dbox{イ}$ の解答群(解答の順序は問わない。)
0: PQ
1: PR
2: QR
3: QT
4: RT
解説
いわゆる「方べきの定理の逆」の話です。
3点 Q, R, T を通る円 O と、P, Q, R を通る直線をかくと、図は次のようになります。
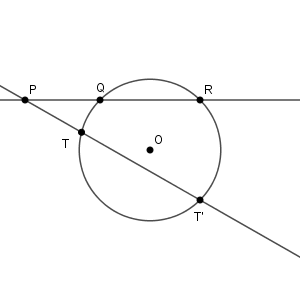
方べきの定理から、\[ \mathrm{ PT }\cdot \mathrm{ PT' }=\mathrm{ PQ }\cdot \mathrm{ PR } \]となります。仮定より $\mathrm{ PQ }\cdot \mathrm{ PR }=\mathrm{ PT }^2$ なので、問題文にある通り、直線 PT が円 O と2点で交わると矛盾します。なので、直線 PT は円 O に接することがいえます。
解答
ア・イ:0・1
解答編 つづき
問題
(2) $\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=\dfrac{1}{2}$, $\mathrm{ BC }=\dfrac{3}{4}$, $\mathrm{ AC }=1$ とする。
このとき、 $\angle \mathrm{ ABC }$ の二等分線と辺 AC との交点を D とすると、 $\mathrm{ AD }=\dfrac{\myBox{ウ} }{\myBox{エ} }$ である。直線 BC 上に、点 C とは異なり、 $\mathrm{ BC }=\mathrm{ BE }$ となる点 E をとる。 $\angle \mathrm{ ABE }$ の二等分線と線分 AE との交点を F とし、直線 AC との交点を G とすると
\begin{eqnarray} \dfrac{\mathrm{ AC } }{\mathrm{ AG } } &=& \dfrac{\myBox{オ} }{\myBox{カ} } \ , \\[5pt] \dfrac{\triangle\mathrm{ ABF }\ \sf{の面積}}{\triangle\mathrm{ AFG }\ \sf{の面積}} &=& \dfrac{\myBox{キ} }{\myBox{ク} } \\[5pt] \end{eqnarray}である。
解説
図は次のようになっています。
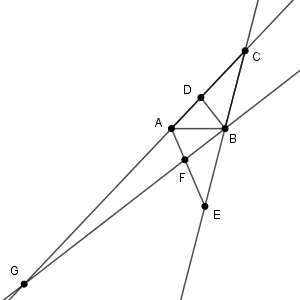
直線 BD は $\angle \mathrm{ ABC }$ の二等分線なので、\[ \mathrm{ AD:CD }=\mathrm{ AB:BC }=2:3 \]となります。なので、\[ \mathrm{ AD }=\dfrac{2}{5}\cdot\mathrm{ AC }=\frac{2}{5} \]となります。
また、外角の二等分線の性質から、 $\mathrm{ AB }:\mathrm{ BC }=\mathrm{ AG }:\mathrm{ GC }$ なので、 $\mathrm{ AG }:\mathrm{ CG }=2:3$ となり、 $\mathrm{ AG }:\mathrm{ AC }=2:1$ となるので\[ \frac{\mathrm{ AC } }{\mathrm{ AG } } = \frac{1}{2} \]と求めることができます。
最後に、三角形 ABF と三角形 AFG の面積比を考えます。 BF, FG を底辺と考えれば高さが同じなので、面積比はこの線分比と一致します。三角形 CGB と直線 AE について、メネラウスの定理を使うと
\begin{eqnarray}
\frac{\mathrm{ CA } }{\mathrm{ AG } } \cdot \frac{\mathrm{ GF } }{\mathrm{ FB } } \cdot \frac{\mathrm{ BE } }{\mathrm{ EC } } &=& 1 \\[5pt]
\frac{1}{2} \cdot \frac{\mathrm{ GF } }{\mathrm{ FB } } \cdot \frac{1}{2} &=& 1 \\[5pt]
\frac{\mathrm{ GF } }{\mathrm{ FB } } &=& 4 \\[5pt]
\end{eqnarray}となります。 $\mathrm{ BF }:\mathrm{ FG }=1:4$ なので、\[ \dfrac{\triangle\mathrm{ ABF }\ \sf{の面積}}{\triangle\mathrm{ AFG }\ \sf{の面積}}=\frac{1}{4} \]となります。
解答
ウエ:25
オカ:12
キク:14
解答編 つづき
問題
線分 DG の中点を H とすると、 $\mathrm{ BH }=\dfrac{\myBox{ケ} }{\myBox{コ} }$ である。また\[ \mathrm{ AH }=\dfrac{\myBox{サ} }{\myBox{シ} }, \ \mathrm{ CH }=\dfrac{\myBox{ス} }{\myBox{セ} } \]である。
解説
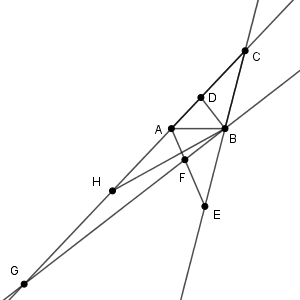
$\angle \mathrm{ DBG }$ に着目すると
\begin{eqnarray}
\angle \mathrm{ DBG }
&=&
\angle \mathrm{ DBA } +\angle \mathrm{ ABG } \\[5pt]
&=&
\frac{1}{2} \angle \mathrm{ ABC } +\frac{1}{2}\angle \mathrm{ ABE } \\[5pt]
&=&
\frac{\angle \mathrm{ ABC }+\angle \mathrm{ ABE } }{2} \\[5pt]
&=&
90^{\circ} \\[5pt]
\end{eqnarray}となります。よって、点 B は、線分 DG を直径とする円周上の点です。また、H はこの円の中心です。そのため、BH は半径だから
\begin{eqnarray}
\mathrm{ BH }
&=&
\frac{\mathrm{ AG }+\mathrm{ AD } }{2} \\[5pt]
&=&
\frac{2+\frac{2}{5} }{2} \\[5pt]
&=&
\frac{10+2}{10} \\[5pt]
&=&
\frac{6}{5} \\[5pt]
\end{eqnarray}となります。また、
\begin{eqnarray}
\mathrm{ AH } &=& \mathrm{ AG }-\mathrm{ HG } \\[5pt]
&=& \mathrm{ AG }-\mathrm{ BH } \\[5pt]
&=& 2-\frac{6}{5} \\[5pt]
&=& \frac{4}{5} \\[5pt]
\end{eqnarray}がわかり、
\begin{eqnarray}
\mathrm{ CH } &=& \mathrm{ CA }+\mathrm{ AH } \\[5pt]
&=& 1+\frac{4}{5} \\[5pt]
&=& \frac{9}{5} \\[5pt]
\end{eqnarray}と求められます。
解答
ケコ:65
サシスセ:4595
解答編 つづき
問題
$\triangle \mathrm{ ABC }$ の外心を O とする。 $\triangle \mathrm{ ABC }$ の外接円 O の半径が $\dfrac{\myBox{ソ}\sqrt{\myBox{タチ} }}{\myBox{ツテ} }$ であることから、線分 BH を $1:2$ に内分する点を I とすると\[ \mathrm{ IO }=\dfrac{\myBox{ト}\sqrt{\myBox{ナ} }}{\myBox{ニヌ} } \]であることがわかる。
解説
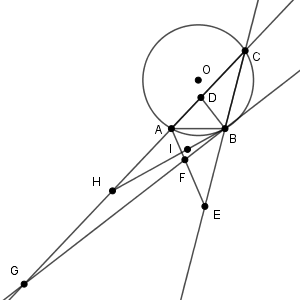
余弦定理より
\begin{eqnarray}
\cos\angle \mathrm{ ABC }
&=&
\frac{\mathrm{ AB }^2+\mathrm{ BC }^2-\mathrm{ AC }^2}{2\cdot \mathrm{ AB }\cdot \mathrm{ BC } } \\[5pt]
&=&
\frac{\frac{1}{4}+\frac{9}{16}-1}{2\cdot \frac{1}{2}\cdot \frac{3}{4} } \\[5pt]
&=&
\frac{\frac{-3}{16} }{\frac{3}{4} } \\[5pt]
&=&
-\frac{1}{4} \\[5pt]
\end{eqnarray}となるので、 $\sin\angle \mathrm{ ABC }=\frac{\sqrt{15} }{4}$ と求められます。円 O の半径を $R$ とすると、正弦定理より
\begin{eqnarray}
2R &=& \frac{\mathrm{ AC } }{\sin\angle \mathrm{ ABC } } \\[5pt]
&=& \frac{1}{\frac{\sqrt{15} }{4} } \\[5pt]
&=& \frac{4}{\sqrt{15} } \\[5pt]
R &=& \frac{2}{\sqrt{15} } \\[5pt]
&=& \frac{2\sqrt{15} }{15} \\[5pt]
\end{eqnarray}となります。
また、 $\mathrm{ HA }\cdot \mathrm{ HC }=\dfrac{36}{25}$, $\mathrm{ HB }^2=\dfrac{36}{25}$ なので、(1)で見た内容から、直線 HB は円 O に接することがわかります。よって、 $\angle \mathrm{ IBO }=\angle \mathrm{ HBO }=90^{\circ}$ が成り立ちます。また、 $\mathrm{ BI }=\dfrac{\mathrm{ BH } }{3}=\dfrac{2}{5}$ なので、三平方の定理から
\begin{eqnarray}
\mathrm{ IO }
&=&
\sqrt{\mathrm{ BI }^2+\mathrm{ BO }^2} \\[5pt]
&=&
\sqrt{\frac{4}{25}+\frac{4}{15} } \\[5pt]
&=&
\sqrt{\frac{12+20}{75} } \\[5pt]
&=&
\frac{\sqrt{32} }{5\sqrt{3} } \\[5pt]
&=&
\frac{4\sqrt{6} }{15} \\[5pt]
\end{eqnarray}と求められます。
解答
ソタチツテ:21515
トナニヌ:4615





