共通テスト 数学I・数学A 2022年度追試 第1問 [3] 解説

【必答問題】

問題編

問題

　三角形は、与えられた辺の長さや角の大きさの条件によって、ただ一通りに決まる場合や二通りに決まる場合がある。

　以下、 $\triangle \mathrm{ ABC }$ において $\mathrm{ AB }=4$ とする。

(1) $\mathrm{ AC }=6$、 $\cos\angle \mathrm{ BAC }=\dfrac{1}{3}$ とする。このとき、 $\mathrm{ BC }=\myBox{ソ}$ であり、 $\triangle \mathrm{ ABC }$ はただ一通りに決まる。

(2) $\sin\angle \mathrm{ BAC }=\dfrac{1}{3}$ とする。このとき、 $\mathrm{ BC }$ の長さのとり得る値の範囲は、点 B と直線 AC との距離を考えることにより、 $\mathrm{ BC }\geqq \dfrac{\myBox{タ} }{\myBox{チ} }$ である。

　$\mathrm{ BC }=\dfrac{\mybox{タ} }{\mybox{チ} }$ または $\mathrm{ BC }=\myBox{ツ}$ のとき、 $\triangle \mathrm{ ABC }$ はただ一通りに決まる。

　また、 $\angle \mathrm{ ABC }=90^{\circ}$ のとき、 $\mathrm{ BC }=\sqrt{\myBox{テ} }$ である。

　したがって、 $\triangle \mathrm{ ABC }$ の形状について、次のことが成り立つ。

・ $\dfrac{\mybox{タ} }{\mybox{チ} } \lt \mathrm{ BC } \lt \sqrt{\mybox{テ} }$ のとき、 $\triangle \mathrm{ ABC }$ は $\dBox{ト}$ 。

・ $\mathrm{ BC }=\sqrt{\mybox{テ} }$ のとき、 $\triangle \mathrm{ ABC }$ は $\dBox{ナ}$ 。

・ $\mathrm{ BC }\gt\sqrt{\mybox{テ} }$ かつ $\mathrm{ BC }\ne \mybox{ツ}$ のとき、 $\triangle \mathrm{ ABC }$ は $\dBox{ニ}$ 。

　$\dbox{ト}$ ～ $\dbox{ニ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: ただ一通りに決まり、それは鋭角三角形である
　1: ただ一通りに決まり、それは直角三角形である
　2: ただ一通りに決まり、それは鈍角三角形である

　3: 二通りに決まり、それらはともに鋭角三角形である
　4: 二通りに決まり、それらは鋭角三角形と直角三角形である
　5: 二通りに決まり、それらは鋭角三角形と鈍角三角形である

　6: 二通りに決まり、それらはともに直角三角形である
　7: 二通りに決まり、それらは直角三角形と鈍角三角形である
　8: 二通りに決まり、それらはともに鈍角三角形である

考え方

(2)が、非常に解きにくいです。計算だけで考えるのは難しいのですが、図をかこうとしてもどのような図をかけばいいのか思いつきにくく、手を付けづらいです。C がどういう場所に存在できるかを考えながら、試行錯誤して図をかきましょう。

【必答問題】

解答編

問題

　三角形は、与えられた辺の長さや角の大きさの条件によって、ただ一通りに決まる場合や二通りに決まる場合がある。

　以下、 $\triangle \mathrm{ ABC }$ において $\mathrm{ AB }=4$ とする。

(1) $\mathrm{ AC }=6$、 $\cos\angle \mathrm{ BAC }=\dfrac{1}{3}$ とする。このとき、 $\mathrm{ BC }=\myBox{ソ}$ であり、 $\triangle \mathrm{ ABC }$ はただ一通りに決まる。

解説

余弦定理より
\begin{eqnarray} \mathrm{ BC }^2 &=& \mathrm{ AB }^2+\mathrm{ AC }^2-2\mathrm{ AB }\cdot\mathrm{ AC }\cos\angle \mathrm{ BAC } \\[5pt] &=& 4^2+6^2-2\cdot 4\cdot 6 \cdot \frac{1}{3} \\[5pt] &=& 16+36-16 \\[5pt] &=& 36 \end{eqnarray}なので、 $\mathrm{ BC }=6$ となります。

解答

ソ：6

解答編 つづき

問題

(2) $\sin\angle \mathrm{ BAC }=\dfrac{1}{3}$ とする。このとき、 $\mathrm{ BC }$ の長さのとり得る値の範囲は、点 B と直線 AC との距離を考えることにより、 $\mathrm{ BC }\geqq \dfrac{\myBox{タ} }{\myBox{チ} }$ である。

解説

$0^{\circ}\lt \theta\lt 180^{\circ}$ で $\sin \theta=\dfrac{1}{3}$ となる $\theta$ は、鋭角と鈍角の2つあります。このうち、小さい方を $\alpha$、大きい方を $\beta$ とします。そうすると、点 C は、下の図の赤線のどこかにあることがわかります。

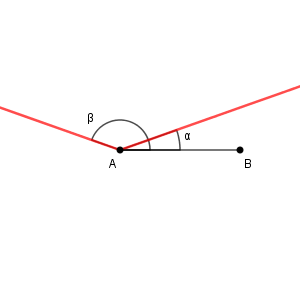
このような点のうち、 BC が最小となるのは、 $\angle \mathrm{ C }=90^{\circ}$ のときです。このときの BC の長さは\[ 4\cdot \sin\angle \mathrm{ BAC }=\dfrac{4}{3} \]と求められるので、 $\mathrm{ BC }\geqq \dfrac{4}{3}$ だとわかります。

なお、計算からも求めることができます。正弦定理より\[ \frac{\mathrm{ AB } }{\sin C}=\dfrac{\mathrm{ BC } }{\sin A} \]が成り立つので、\[ \mathrm{ BC }=\dfrac{4}{3\sin C} \]となります。 $C=90^{\circ}$ となることはあるので、このときに最小値 $\dfrac{4}{3}$ をとることがわかります。

解答

タチ：43

解答編 つづき

問題

　$\mathrm{ BC }=\dfrac{\mybox{タ} }{\mybox{チ} }$ または $\mathrm{ BC }=\myBox{ツ}$ のとき、 $\triangle \mathrm{ ABC }$ はただ一通りに決まる。

　また、 $\angle \mathrm{ ABC }=90^{\circ}$ のとき、 $\mathrm{ BC }=\sqrt{\myBox{テ} }$ である。

解説

BC の長さを決めたときに C の場所がどこかになりうるかを考えます。そのために、B を中心とする円をかくことにします。

$\mathrm{ BC }=\dfrac{4}{3}$ の場合は以下のようになります。このときは、右側の赤い線が円の接線になります。

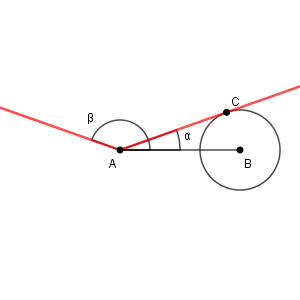
なので、問題文にあるように、たしかに C の場所は1点に決まり、三角形 ABC の形状は1通りに決まることがわかります。

これよりも少し大きくなると、次のようになります。

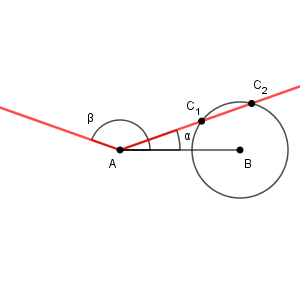
赤い線と2点で交わります。 C は、2点のどちらにあっても、今考えている条件（ AB の長さと $\sin\angle \mathrm{ BAC }$ の値）を満たすため、三角形 ABC の形状は二通りあることがわかります。

ただ、この円の半径をどんどん大きくしていくと、次のような状況が現れます。

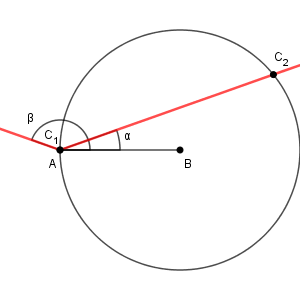
先ほどの $\mathrm{ C }_1$ が A に一致してしまうときです。このとき、3点 $\mathrm{ A }, \mathrm{ B }, \mathrm{ C }_1$ を結んでも三角形はできません。そのため、この場合は、 C は $\mathrm{ C }_2$ にある場合しか三角形はできないので、三角形 ABC の形状は一通りに決まります。

こうなってしまうのは、半径が AB と一致するとき、つまり、 $\mathrm{ BC }=4$ のときです。

さらに半径を大きくすると、左側の赤い線と右側の赤い線で、それぞれ1点ずつ交点をもつので、三角形 ABC の形状は二通りあることがわかります。

以上から、 $\mathrm{ BC }=\dfrac{4}{3},4$ のときは、$\triangle \mathrm{ ABC }$ はただ一通りに決まることがわかります。

また、 $\angle \mathrm{ ABC }=90^{\circ}$ のとき、 $\mathrm{ AC }:\mathrm{ BC }=3:1$ なので、\[ \mathrm{ AB }:\mathrm{ BC }=\sqrt{3^2-1^2}:1=2\sqrt{2}:1 \]であり、 $\mathrm{ AB }=4$ なので、 $\mathrm{ BC }=\sqrt{2}$ と求められます。

解答

ツ：4
テ：2

解答編 つづき

問題

　したがって、 $\triangle \mathrm{ ABC }$ の形状について、次のことが成り立つ。

・ $\dfrac{\mybox{タ} }{\mybox{チ} } \lt \mathrm{ BC } \lt \sqrt{\mybox{テ} }$ のとき、 $\triangle \mathrm{ ABC }$ は $\dBox{ト}$ 。

・ $\mathrm{ BC }=\sqrt{\mybox{テ} }$ のとき、 $\triangle \mathrm{ ABC }$ は $\dBox{ナ}$ 。

・ $\mathrm{ BC }\gt\sqrt{\mybox{テ} }$ かつ $\mathrm{ BC }\ne \mybox{ツ}$ のとき、 $\triangle \mathrm{ ABC }$ は $\dBox{ニ}$ 。

　$\dbox{ト}$ ～ $\dbox{ニ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: ただ一通りに決まり、それは鋭角三角形である
　1: ただ一通りに決まり、それは直角三角形である
　2: ただ一通りに決まり、それは鈍角三角形である

　3: 二通りに決まり、それらはともに鋭角三角形である
　4: 二通りに決まり、それらは鋭角三角形と直角三角形である
　5: 二通りに決まり、それらは鋭角三角形と鈍角三角形である

　6: 二通りに決まり、それらはともに直角三角形である
　7: 二通りに決まり、それらは直角三角形と鈍角三角形である
　8: 二通りに決まり、それらはともに鈍角三角形である

解説

まず、 $\dfrac{4}{3}\lt \mathrm{ BC } \lt \sqrt{2}$ の場合を考えます。

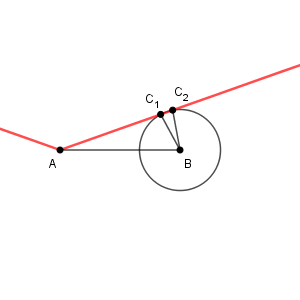
この場合、 B を中心とし、半径を BC と同じ長さとした円をかくと、$\dfrac{4}{3}\lt \mathrm{ BC }$ なので、赤い線と2点で交わります。 A に近い方から順に $\mathrm{ C }_1, \mathrm{ C }_2$ とします。

このとき、 $\angle \mathrm{ AC_1B }$ は鈍角で、 $\angle \mathrm{ AC_2B }$ は鋭角です。また、 $\mathrm{ BC }\lt \sqrt{2}$ なので、どちらの場合でも $B$ は鋭角です。そのため、 $\triangle \mathrm{ ABC }$ は二通りに決まり、それらは鈍角三角形と鋭角三角形であることがわかります。

$\mathrm{ BC }=\sqrt{2}$ のときは、三角形 $\mathrm{ ABC }_2$ が直角三角形となります。そのため、 $\triangle \mathrm{ ABC }$ は二通りに決まり、それらは鈍角三角形と直角三角形であることがわかります。

また、 $\sqrt{2} \lt \mathrm{ BC } \lt 4$ のときは、$\angle\mathrm{ AC_1B },\ \angle\mathrm{ ABC_2 }$ が鈍角となります。

そのため、 $\triangle \mathrm{ ABC }$ は二通りに決まり、それらはともに鈍角三角形であることがわかります。

最後に、 $\mathrm{ BC } \gt 4$ のときは、$\angle\mathrm{ C_1AB },\ \angle\mathrm{ ABC_2 }$ が鈍角となります。

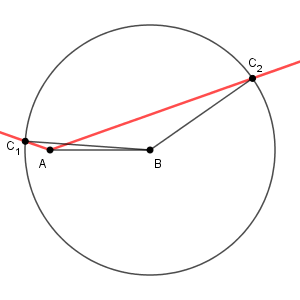
そのため、 $\triangle \mathrm{ ABC }$ は二通りに決まり、それらはともに鈍角三角形であることがわかります。

こうして、$\mathrm{ BC }\gt\sqrt{2}$ かつ $\mathrm{ BC }\ne 4$ のときは、 $\triangle \mathrm{ ABC }$ は二通りに決まり、それらはともに鈍角三角形であることがわかります。

解答

ト：5
ナ：7
ニ：8