共通テスト 数学I・数学A 2022年度追試 第2問 [2] 解説
【必答問題】
問題編
問題
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数(以下、交通量という。単位は台)を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値(以下、速度という。単位は km/h)を用いる。
(1) 表1は、2015年の交通量と速度の平均値、標準偏差および共分散である。ただし、共分散は交通量の偏差と速度の偏差の積の平均値である。
表1 2015年の交通量と速度の平均値、標準偏差および共分散 平均値 標準偏差 共分散 交通量 $17300$ $10200$ $-63600$ 速度 $82.0$ $9.60$ この表より、(標準偏差):(平均値)の比の値は、小数第3位を四捨五入すると、交通量については $0.59$ であり、速度については $\dBox{テ}$ である。また、交通量と速度の相関係数は $\dBox{ト}$ である。
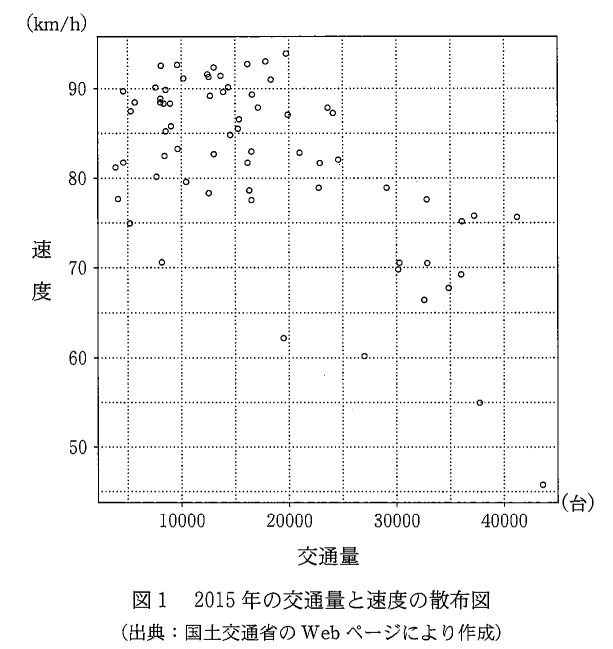
また、図1は、2015年の交通量と速度の散布図である。なお、この散布図には、完全に重なっている点はない。
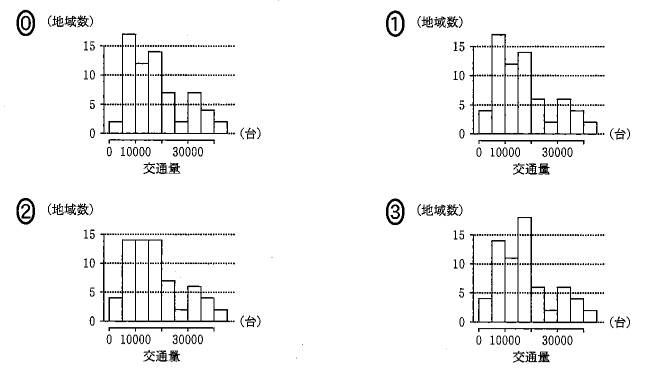
2015年の交通量のヒストグラムは、図1を参考にすると、 $\dBox{ナ}$ である。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。また、表1および図1から読み取れることとして、後の 0 ~ 5 のうち、正しいものは $\dBox{ニ}$ と $\dBox{ヌ}$ である。
$\dbox{テ}$, $\dbox{ト}$ については、最も適当なものを、次の 0 ~ 9 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $-0.71$
1: $-0.65$
2: $-0.59$
3: $-0.12$
4: $-0.03$5: $0.03$
6: $0.12$
7: $0.59$
8: $0.65$
9: $0.71$$\dbox{ナ}$ の解答群
$\dbox{ニ}$, $\dbox{ヌ}$ の解答群(解答の順序は問わない。)
0: 交通量が $27500$ 以上のすべての地域の速度は $75$ 未満である。
1: 交通量が $10000$ 未満のすべての地域の速度は $70$ 以上である。
2: 速度が平均値以上のすべての地域では、交通量が平均値以上である。
3: 速度が平均値未満のすべての地域では、交通量が平均値未満である。
4: 交通量が $27500$ 以上の地域は、ちょうど 7地域存在する。
5: 速度が $72.5$ 未満の地域は、ちょうど 11地域存在する。
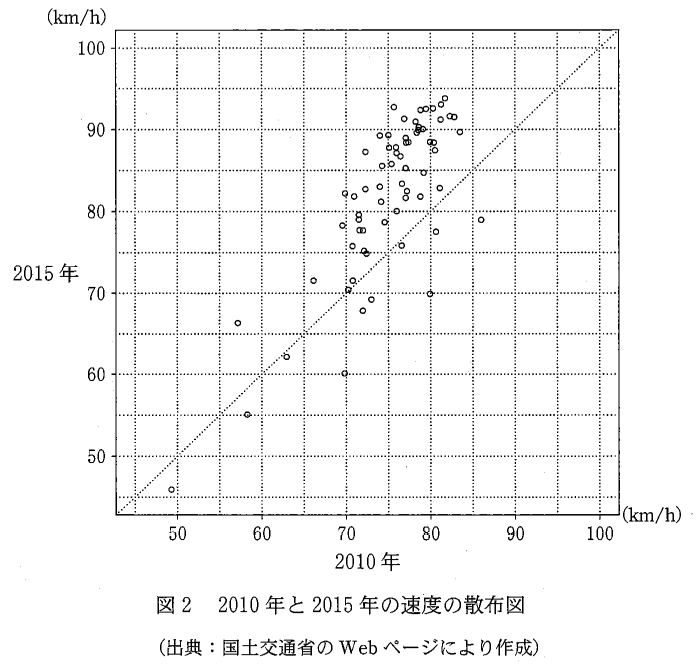
(2) 図2は、2010年と2015年の速度の散布図である。ただし、原点を通り、傾きが $1$ である直線(点線)を補助的に描いている。また、この散布図には、完全に重なっている点はない。
67地域について、2010年より2015年の速度が速くなった地域群をA群、遅くなった地域群をB群とする。A群の地域数は $\myBox{ネノ}$ である。
B群において、2010年より2015年の速度が、5km/h 以上遅くなった地域数は $\myBox{ハ}$ であり、10%以上遅くなった地域数は $\myBox{ヒ}$ である。
A群の2015年の速度については、第1四分位数は $81.2$、中央値は $86.7$、第3四分位数は $89.7$ であた。次の (I)、(II)、(III) はA群とB群の2015年の速度に関する記述である。
(I) A群の速度の範囲は、B群の速度の範囲より小さい。
(II) A群の速度の第1四分位数は、B群の速度の第3四分位数より小さい。
(III) A群の速度の四分位範囲は、B群の速度の四分位範囲より小さい。
(I)、(II)、(III) の正誤の組合せとして正しいものは $\dBox{フ}$ である。
$\dbox{フ}$ の解答群
0: (I) 正 (II) 正 (III) 正
1: (I) 正 (II) 正 (III) 誤
2: (I) 正 (II) 誤 (III) 正
3: (I) 正 (II) 誤 (III) 誤4: (I) 誤 (II) 正 (III) 正
5: (I) 誤 (II) 正 (III) 誤
6: (I) 誤 (II) 誤 (III) 正
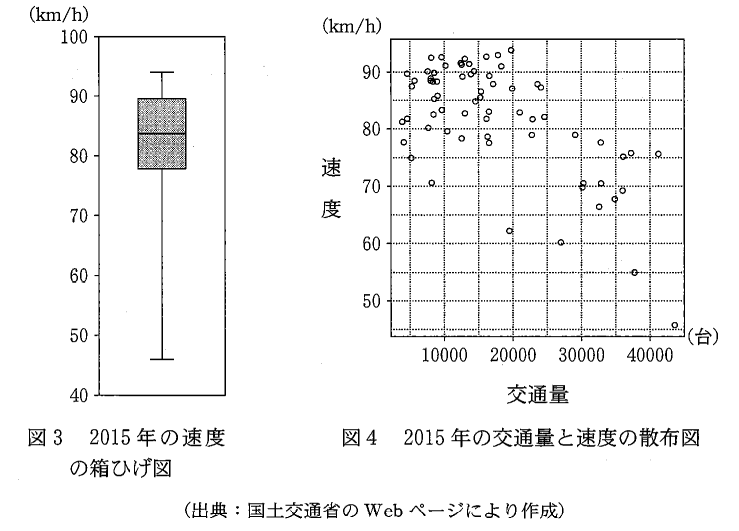
7: (I) 誤 (II) 誤 (III) 誤(3) 図3は2015年の速度の箱ひげ図である。図4は図1を再渇したものであり、2015年の交通量と速度の散布図である。これらの速度から 1km あたりの走行時間(分) を考える。例えば、速度が $55$ km/h の場合は、1時間あたりの走行距離が $55$ km なので、1kmあたりの走行時間は $\dfrac{1}{55}\times 60$ の小数第3位を四捨五入して $1.09$ 分となる。
このようにして2015年の速度を 1km あたりの走行時間に変換したデータの箱ひげ図は $\dBox{ヘ}$ であり、2015年の交通量と 1km あたりの走行時間の散布図は $\dBox{ホ}$ である。なお、解答群の散布図には、完全に重なっている点はない。
$\dbox{へ}$ の解答群
$\dbox{ホ}$ の解答群
考え方
(1)は、データの分析で出てくる基本的な内容がわかっているかどうかを問う問題ですが、量が多く、盛りだくさんです。
(2)は、点線でかかれたものをどう使うかを考えます。また、他の問題を解くときには、自分で必要な線を追加して考えましょう。
(3)はデータの変換によって、箱ひげ図や散布図がどう変わるかを考える問題です。特徴的な値について、変換の前後でどのように値が変わるかを考えながら選択肢をしぼっていきましょう。
【必答問題】
解答編
問題
国土交通省では「全国道路・街路交通情勢調査」を行い、地域ごとのデータを公開している。以下では、2010年と2015年に67地域で調査された高速道路の交通量と速度を使用する。交通量としては、それぞれの地域において、ある1日にある区間を走行した自動車の台数(以下、交通量という。単位は台)を用いる。また、速度としては、それぞれの地域において、ある区間を走行した自動車の走行距離および走行時間から算出した値(以下、速度という。単位は km/h)を用いる。
(1) 表1は、2015年の交通量と速度の平均値、標準偏差および共分散である。ただし、共分散は交通量の偏差と速度の偏差の積の平均値である。
表1 2015年の交通量と速度の平均値、標準偏差および共分散 平均値 標準偏差 共分散 交通量 $17300$ $10200$ $-63600$ 速度 $82.0$ $9.60$ この表より、(標準偏差):(平均値)の比の値は、小数第3位を四捨五入すると、交通量については $0.59$ であり、速度については $\dBox{テ}$ である。また、交通量と速度の相関係数は $\dBox{ト}$ である。
また、図1は、2015年の交通量と速度の散布図である。なお、この散布図には、完全に重なっている点はない。
2015年の交通量のヒストグラムは、図1を参考にすると、 $\dBox{ナ}$ である。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。また、表1および図1から読み取れることとして、後の 0 ~ 5 のうち、正しいものは $\dBox{ニ}$ と $\dBox{ヌ}$ である。
$\dbox{テ}$, $\dbox{ト}$ については、最も適当なものを、次の 0 ~ 9 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $-0.71$
1: $-0.65$
2: $-0.59$
3: $-0.12$
4: $-0.03$5: $0.03$
6: $0.12$
7: $0.59$
8: $0.65$
9: $0.71$$\dbox{ナ}$ の解答群
$\dbox{ニ}$, $\dbox{ヌ}$ の解答群(解答の順序は問わない。)
0: 交通量が $27500$ 以上のすべての地域の速度は $75$ 未満である。
1: 交通量が $10000$ 未満のすべての地域の速度は $70$ 以上である。
2: 速度が平均値以上のすべての地域では、交通量が平均値以上である。
3: 速度が平均値未満のすべての地域では、交通量が平均値未満である。
4: 交通量が $27500$ 以上の地域は、ちょうど 7地域存在する。
5: 速度が $72.5$ 未満の地域は、ちょうど 11地域存在する。
解説
まず、標準偏差と平均値の比を考えます。問題文にある通り、交通量については、比の値は\[ \dfrac{10200}{17300}=0.589\cdots \]となり、たしかに四捨五入すれば $0.59$ となります。速度については\[ \frac{9.60}{82.0}=0.117\cdots \]なので、小数第3位を四捨五入すれば、 $0.12$ と求められます。
相関係数は、共分散をそれぞれの標準偏差で割って求めることができるので\[ \dfrac{-63600}{10200\times 9.6}=-0.649\cdots \]となり、選択肢の中では $-0.65$ が一番近いことがわかります。
次に、ナのヒストグラムを考えます。一番左の 5000~10000 のところを見ると、4点あるので、選択肢0ではないことがわかります。15000~20000 のところを見ると、14点あるので、選択肢3ではないことがわかります。
残りは1と2ですが、20000~25000 のところを見てみます。6点あるので、選択肢2ではないことがわかります。こうして、選択肢1だとしぼることができます。
最後に、ニとヌを考えます。順番に考えていきます。
選択肢0は、散布図を見ると、交通量が32500で速度が75より大きい点があるので、誤りです。
選択肢1は、散布図を見ると、交通量が10000より左にある点は、すべて速度が70より大きいことがわかるので、正しいです。
次に、選択肢2と3を考えます。表1より、速度の平均値が $82.0$ ですが、これより大きいところで交通量が平均値の $17300$ を下回っている点があります(例えば、交通量 $5000$ 、速度 $90$ あたりの点)。また、速度が平均値より小さく、交通量が平均値より大きい点もあります(例えば、交通量 $37500$ 、速度 $55$ あたりの点)。なので、どちらの選択肢も誤りです。
選択肢4は、交通量が $27500$ 以上の点を数えると、7よりも多いので誤りです。
選択肢5は、速度が $72.5$ 未満の点を数えると、11なので、正しいです。
よって、選択肢 1 と 5 が正しいとわかります。
解答
テ:6
ト:1
ナ:1
ニ:ヌ:1・5
解答編 つづき
問題
(2) 図2は、2010年と2015年の速度の散布図である。ただし、原点を通り、傾きが $1$ である直線(点線)を補助的に描いている。また、この散布図には、完全に重なっている点はない。
67地域について、2010年より2015年の速度が速くなった地域群をA群、遅くなった地域群をB群とする。A群の地域数は $\myBox{ネノ}$ である。
B群において、2010年より2015年の速度が、5km/h 以上遅くなった地域数は $\myBox{ハ}$ であり、10%以上遅くなった地域数は $\myBox{ヒ}$ である。
A群の2015年の速度については、第1四分位数は $81.2$、中央値は $86.7$、第3四分位数は $89.7$ であた。次の (I)、(II)、(III) はA群とB群の2015年の速度に関する記述である。
(I) A群の速度の範囲は、B群の速度の範囲より小さい。
(II) A群の速度の第1四分位数は、B群の速度の第3四分位数より小さい。
(III) A群の速度の四分位範囲は、B群の速度の四分位範囲より小さい。
(I)、(II)、(III) の正誤の組合せとして正しいものは $\dBox{フ}$ である。
$\dbox{フ}$ の解答群
0: (I) 正 (II) 正 (III) 正
1: (I) 正 (II) 正 (III) 誤
2: (I) 正 (II) 誤 (III) 正
3: (I) 正 (II) 誤 (III) 誤4: (I) 誤 (II) 正 (III) 正
5: (I) 誤 (II) 正 (III) 誤
6: (I) 誤 (II) 誤 (III) 正
7: (I) 誤 (II) 誤 (III) 誤
解説
散布図では、横軸が2010年の速度を、縦軸が2015年の速度を表しています。それぞれを $x, y$ とおいて考えることにしましょう。
2010年より2015年の速度が速くなった、ということは、 $y\gt x$ ということであり、散布図でいうと、点線よりも上にある、ということです。なので、A群の地域数は、点線より上にある点を数えればいいです。
しかし、これは多すぎるので、B群を数えて全体から引きましょう。B群の地域数は数えると $10$ だとわかるので、A群の地域数は $67-10=57$ と求められます。
次に、2010年より2015年の速度が 5km/h 以上遅くなった、という条件を考えます。これは式でいうと $y\leqq x-5$ です。そのため、点線を下に $5$ だけずらした直線より下にある点を数えればいいです。散布図に直線をかきこんで数えると、 $(70, 60)$, $(80,70)$, $(86,79)$ あたりにある3点だけだとわかります。
また、10%以上遅くなった地域を数えます。2010年での速度が $50$ 以上なら、 $5$ 以上値が小さくなっているはずです。なので、先ほど求めた3点と、$(49, 46)$ あたりの点だけを考えればいいです。そうすると、2015年に 10% 以上下がったのは、 $(70, 60)$, $(80,70)$ あたりにある2点だけだとわかります。
続いて、3つの文章について考えます。
2015年のB群とは、点線より下にある点の $y$ 座標について考えるということです。
A群の速度の最小値は $67$ あたりで、最大値は $94$ あたりなので、範囲はおよそ $27$ です。B群の速度の最小値は $46$ あたりで、最大値は $79$ あたりなので、範囲はおよそ $33$ です。よって、A群の速度の範囲のほうが小さく、(I)は正しいとわかります。
B群の速度の第3四分位数とは、データの数が10個なので、上から3番目の値です。およそ $76$ です。A群の速度の第1四分位数は、問題文より $81.2$ なので、B群の速度の第3四分位数より大きいです。(II)は誤りです。
B群の速度の第1四分位数は、下から3番目の値であり、およそ $60$ です。なので、B群の四分位範囲は、およそ $76-60=16$ です。A群の四分位範囲は、 $89.7-81.2=8.5$ なので、A群の四分位範囲のほうが小さいので、(III)は正しいです。
よって、(I), (II), (III) の正誤は、順番に、正・誤・正となります。
解答
ネノ:57
ハ:3
ヒ:2
フ:2
解答編 つづき
問題
(3) 図3は2015年の速度の箱ひげ図である。図4は図1を再渇したものであり、2015年の交通量と速度の散布図である。これらの速度から 1km あたりの走行時間(分) を考える。例えば、速度が $55$ km/h の場合は、1時間あたりの走行距離が $55$ km なので、1kmあたりの走行時間は $\dfrac{1}{55}\times 60$ の小数第3位を四捨五入して $1.09$ 分となる。
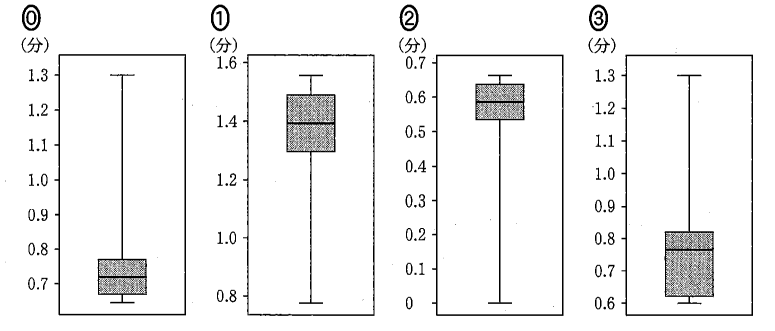
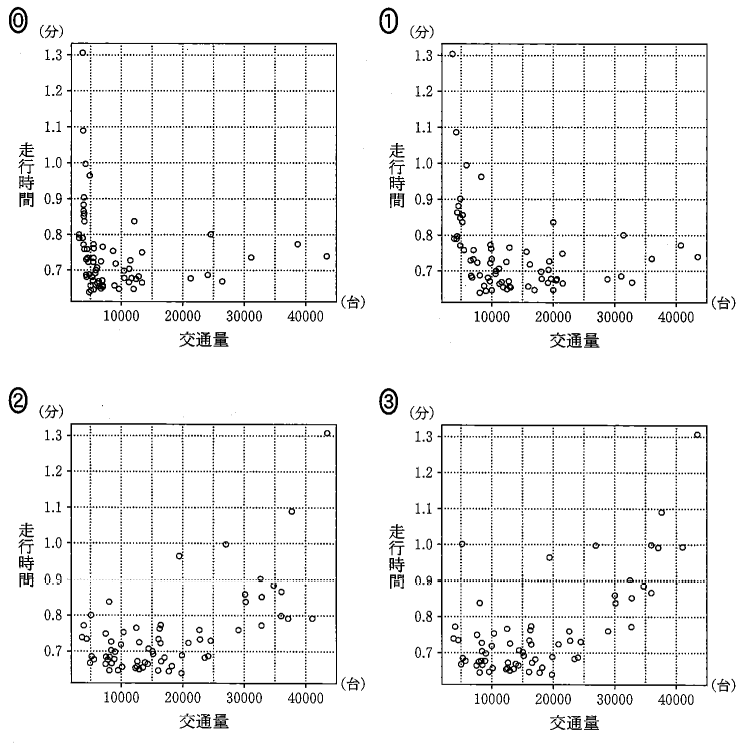
このようにして2015年の速度を 1km あたりの走行時間に変換したデータの箱ひげ図は $\dBox{ヘ}$ であり、2015年の交通量と 1km あたりの走行時間の散布図は $\dBox{ホ}$ である。なお、解答群の散布図には、完全に重なっている点はない。
$\dbox{へ}$ の解答群
$\dbox{ホ}$ の解答群
解説
速度が速い方が、1kmあたりの走行時間は短くなります(式からもわかりますが、直感的にもわかるはずです)。そのため、変換後の箱ひげ図の最小値には、変換前の箱ひげ図の最大値が対応します。
変換前の箱ひげ図の最大値は、94くらいなので、1kmあたりの走行時間になおすと\[ \frac{1}{94}\times 60=0.638\cdots \]となります。93や95に変えても、0.63 や 0.64 くらいになるので、箱ひげ図は選択肢 0 が正しいとわかります。(0.6 のところに目盛りがないのはイマイチですが)
最後に、散布図を選びます。交通量は何も変わっていないので、35000~40000には、4点あるはずなので、選択肢0と選択肢1は誤りだとすぐにわかります。
選択肢2と3を比較してわかりやすい違いを探します。すると、選択肢3には、交通量が5000で走行時間が1分の所に点があることがわかります。1kmあたり1分ということは、1時間で60kmなので、60km/h ですが、もとの散布図にはそのような点はありません。なので、選択肢3も誤りです。
こうして、選択肢2が正しいとわかります。
解答
ヘホ:02