共通テスト数学I・数学A 2022年度追試第2問 [1] 解説

🕒 2022/02/05 🔄 2023/05/01

【必答問題】

問題編

問題

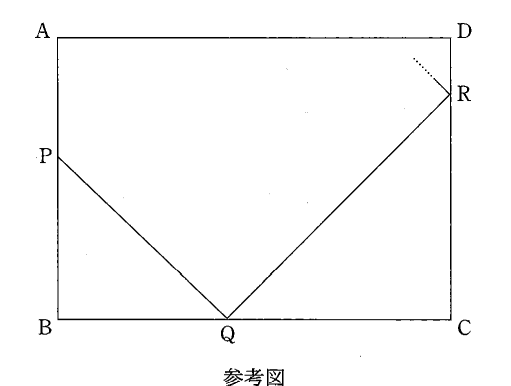
　$a$ を $5\lt a \lt 10$ を満たす実数とする。長方形 ABCD を考え、 $\mathrm{ AB }=\mathrm{ CD }=5$、 $\mathrm{ BC }=\mathrm{ DA }=a$ とする。

　次のようにして、長方形 ABCD の辺上に4点 P, Q, R, S をとり、内部に点 T をとることを考える。

　辺 AB 上に点 B と異なる点 P をとる。辺 BC 上に点 Q を $\angle \mathrm{ BPQ }$ が $45^{\circ}$ になるようにとる。 Q を通り、直線 PQ と垂直に交わる直線を $\ell$ とする。 $\ell$ が頂点 C, D 以外の点で辺 CD と交わるとき、 $\ell$ と辺 CD の交点を R とする。

　点 R を通り $\ell$ と垂直に交わる直線を $m$ とする。 $m$ と辺 AD との交点を S とする。点 S を通り $m$ と垂直に交わる直線を $n$ とする。 $n$ と直線 PQ との交点を T とする。

(1) $a=6$ のとき、 $\ell$ が頂点 C, D 以外の点で辺 CD と交わるときの AP の値の範囲は $0\leqq \mathrm{ AP }\lt\myBox{ア}$ である。このとき、四角形 QRST の面積の最大値は $\dfrac{\myBox{イウ} }{\myBox{エ} }$ である。

　$a=8$ のとき、四角形 QRST の面積の最大値は $\myBox{オカ}$ である。

(2) $5\lt a \lt 10$ とする。 $\ell$ が頂点 C, D 以外の点で辺 CD と交わるときの AP の値の範囲は\[ 0\leqq \mathrm{ AP }\lt \myBox{キク}-a \quad\cdots① \]である。

　点 P が①を満たす範囲を動くとする。四角形 QRST の面積の最大値が $\dfrac{\mybox{イウ} }{\mybox{エ} }$ となるときの $a$ の値の範囲は\[ 5\lt a\leqq \frac{\myBox{ケコ} }{\myBox{サ} } \]である。

　$a$ が $\dfrac{\mybox{ケコ} }{\mybox{サ} } \lt a \lt 10$ を満たすとき、 P が①を満たす範囲を動いたときの四角形 QRST の面積の最大値は\[ \myBox{シス}a^2 +\myBox{セソ}a-\myBox{タチツ} \]である。

考え方

AP と $a$ 、2つの文字があるため、考えづらいです。そのうえ、図形ともからんでいるので、なかなかハードルが高いです。

$x$ 以外の文字が入った二次関数の最大・最小を考える問題はよく出題されており、この問題も一応その類題といえますが、後半で「最大値が〇〇となるときの $a$ の値の範囲は…」など、さらにひねった設定になっています。

(2)の結果は、(1)の結果で検算できるとはいえ、考察も計算も時間内にやるのは大変です。(1)の計算をよく見ながら(2)を考えましょう。

【必答問題】

解答編

問題

　$a$ を $5\lt a \lt 10$ を満たす実数とする。長方形 ABCD を考え、 $\mathrm{ AB }=\mathrm{ CD }=5$、 $\mathrm{ BC }=\mathrm{ DA }=a$ とする。

　次のようにして、長方形 ABCD の辺上に4点 P, Q, R, S をとり、内部に点 T をとることを考える。

　辺 AB 上に点 B と異なる点 P をとる。辺 BC 上に点 Q を $\angle \mathrm{ BPQ }$ が $45^{\circ}$ になるようにとる。 Q を通り、直線 PQ と垂直に交わる直線を $\ell$ とする。 $\ell$ が頂点 C, D 以外の点で辺 CD と交わるとき、 $\ell$ と辺 CD の交点を R とする。

　点 R を通り $\ell$ と垂直に交わる直線を $m$ とする。 $m$ と辺 AD との交点を S とする。点 S を通り $m$ と垂直に交わる直線を $n$ とする。 $n$ と直線 PQ との交点を T とする。

(1) $a=6$ のとき、 $\ell$ が頂点 C, D 以外の点で辺 CD と交わるときの AP の値の範囲は $0\leqq \mathrm{ AP }\lt\myBox{ア}$ である。このとき、四角形 QRST の面積の最大値は $\dfrac{\myBox{イウ} }{\myBox{エ} }$ である。

解説

$\mathrm{ AP }=x$ とおくと、 $\mathrm{ BP }=5-x$ で、 $\mathrm{ BQ }=5-x$ となります（三角形 BPQ が直角二等辺三角形だから）。よって、 $\mathrm{ CQ }=6-(5-x)=x+1$ となります。

これが $5$ より小さければ、直線 $\ell$ は、辺 CD と端点以外で交わります。 $x+1\lt 5$ より $x\lt 4$ となります。よって、 AP の値の範囲は\[ 0\leqq \mathrm{ AP } \lt 4 \]となります。

このとき、 $\mathrm{ DR }=5-(x+1)=4-x$ となります。四角形 QRST は長方形だから、面積は
\begin{eqnarray} & & \mathrm{ QR }\cdot \mathrm{ SR } \\[5pt] &=& \sqrt{2} (x+1)\cdot \sqrt{2} (4-x) \\[5pt] &=& 2(-x^2+3x+4) \\[5pt] &=& -2(x^2-3x)+8 \\[5pt] &=& -2\left(x-\frac{3}{2}\right)^2 +\frac{9}{2}+8 \\[5pt] &=& -2\left(x-\frac{3}{2}\right)^2 +\frac{25}{2} \\[5pt] \end{eqnarray}となります。 $0\leqq x \lt 4$ なので、 $x=\dfrac{3}{2}$ のときに面積は最大値 $\dfrac{25}{2}$ をとることがわかります。

解答

ア：4
イウエ：252

解答編　つづき

問題

　$a=8$ のとき、四角形 QRST の面積の最大値は $\myBox{オカ}$ である。

解説

$a=8$ のときも、 $a=6$ のときと同様にします。

$\mathrm{ AP }=x$ とおくと、 $\mathrm{ BP }=\mathrm{ BQ }=5-x$ です。よって、 $\mathrm{ CQ }=8-(5-x)=x+3$ となります。 $x+3\lt 5$ を解くと $x\lt 2$ となるので、 $0\leqq x \lt 2$ となります。

このとき、 $\mathrm{ DR }=5-(x+3)=2-x$ となります。四角形 QRST は長方形だから、面積は
\begin{eqnarray} & & \mathrm{ QR }\cdot \mathrm{ SR } \\[5pt] &=& \sqrt{2} (x+3)\cdot \sqrt{2} (2-x) \\[5pt] &=& 2(-x^2-x+6) \\[5pt] &=& -2(x^2+x)+12 \\[5pt] &=& -2\left(x+\frac{1}{2}\right)^2 +\frac{1}{2}+12 \\[5pt] &=& -2\left(x+\frac{1}{2}\right)^2 +\frac{25}{2} \\[5pt] \end{eqnarray}となります。 $0\leqq x \lt 2$ の範囲では単調に減少するので、 $x=0$ のときに最大値 $12$ をとることがわかります。

解答

オカ：12

解答編　つづき

問題

(2) $5\lt a \lt 10$ とする。 $\ell$ が頂点 C, D 以外の点で辺 CD と交わるときの AP の値の範囲は\[ 0\leqq \mathrm{ AP }\lt \myBox{キク}-a \quad\cdots① \]である。

　点 P が①を満たす範囲を動くとする。四角形 QRST の面積の最大値が $\dfrac{\mybox{イウ} }{\mybox{エ} }$ となるときの $a$ の値の範囲は\[ 5\lt a\leqq \frac{\myBox{ケコ} }{\myBox{サ} } \]である。

　$a$ が $\dfrac{\mybox{ケコ} }{\mybox{サ} } \lt a \lt 10$ を満たすとき、 P が①を満たす範囲を動いたときの四角形 QRST の面積の最大値は\[ \myBox{シス}a^2 +\myBox{セソ}a-\myBox{タチツ} \]である。

解説

(1)のときと同様にします。

$\mathrm{ AP }=x$ とおくと、 $\mathrm{ BP }=\mathrm{ BQ }=5-x$ です。よって、 $\mathrm{ CQ }=a-(5-x)=x+a-5$ となります。 $x+a-5\lt 5$ を解くと $x\lt 10-a$ となるので、 $0\leqq \mathrm{AP} \lt 10-a$ となります。

このとき、 $\mathrm{ DR }=5-(x+a-5)=-x-a+10$ となります。四角形 QRST は長方形だから、面積は
\begin{eqnarray} & & \mathrm{ QR }\cdot \mathrm{ SR } \\[5pt] &=& \sqrt{2} (x+a-5)\cdot \sqrt{2} (-x-a+10) \\[5pt] &=& 2\{ -x^2 +(-a+10-a+5)x+(a-5)(-a+10) \} \\[5pt] &=& 2\{ -x^2 +(-2a+15)x\}+2(a-5)(-a+10) \\[5pt] &=& -2\left(x-\frac{-2a+15}{2}\right)^2 +\frac{(-2a+15)^2}{2}+2(a-5)(-a+10) \\[5pt] &=& -2\left(x-\frac{-2a+15}{2}\right)^2 +\frac{4a^2-60a+225}{2}+2(-a^2+15a-50) \\[5pt] &=& -2\left(x-\frac{-2a+15}{2}\right)^2 +\frac{25}{2} \\[5pt] \end{eqnarray}となります。

いつ最大値をとるかは、放物線の軸や頂点と、 $x$ のとりうる範囲によって変わります。

$\dfrac{-2a+15}{2}\geqq 0$ のとき、つまり $a\leqq \dfrac{15}{2}$ のときは、頂点で最大値をとります。つまり、 $x=\dfrac{-2a+15}{2}$ で最大値 $\dfrac{25}{2}$ をとることがわかります。

一方、 $\dfrac{-2a+15}{2}\lt 0$ のとき、つまり、 $a\gt \dfrac{15}{2}$ のときは、区間の左端で最大値をとります。つまり、 $x=0$ のときに最大値\[ 2(a-5)(-a+10)=-2a^2+30a-100 \]をとることがわかります。この値は頂点の $y$ 座標 $\dfrac{25}{2}$ より必ず小さくなります。

よって、四角形 QRST の面積の最大値が $\dfrac{25}{2}$ となるような $a$ の値の範囲は $5\lt a \leqq \dfrac{15}{2}$ であり、 $\dfrac{25}{2}\lt a \lt 10$ のときの面積の最大値は $-2a^2+30a-100$ となります。