共通テスト 数学I・数学A 2022年度追試 第1問 [2] 解説

【必答問題】
（三角比の表は省略しています）

問題編

問題

　以下の問題を解答するにあたっては、必要に応じて33ページの三角比の表を用いてもよい。

　火災時にビルの高層階に取り残された人を救出する際、はしご車を使用することがある。

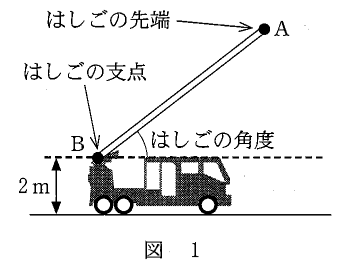
　図１のはしご車で考える。はしごの先端を A、はしごの支点を B とする。はしごの角度（はしごと水平面のなす角の大きさ）は $75^{\circ}$ まで大きくすることができ、はしごの長さ AB は $35$ mまで伸ばすことができる。また、はしごの支点 B は地面から $2$ mの高さにあるとする。

　以下、はしごの長さ AB は $35$ mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。

(1) はしごの先端 A の最高到達点の高さは、地面から $\myBox{サシ}$ mである。小数第1位を四捨五入して答えよ。

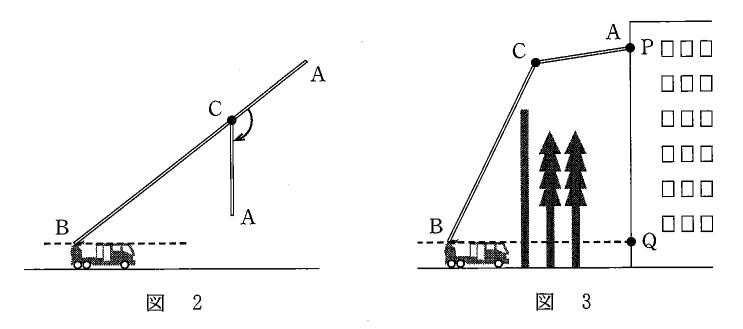
(2) 図１のはしごは、図２のように、点 C で、AC が鉛直方向になるまで下向きに屈折させることができる。AC の長さは $10$ mである。

　図３のように、あるビルにおいて、地面から $26$ mの高さにある位置を点 P とする。障害物のフェンスや木があるため、はしご車を BQ の長さが $18$ mとなる場所にとめる。ここで、点 Q は、点 P の真下で、点 B と同じ高さにある位置である。

　このとき、はしごの先端 A が点 P に届くかどうかは、障害物の高さや、はしご車と障害物の距離によって決まる。そこで、このことについて、後の(i)、(ii)のように考える。

　ただし、はしご車、障害物、ビルは同じ水平な地面上にあり、点 A, B, C, P, Q はすべて同一平面上にあるものとする。

(i) はしごを点 C で屈折させ、はしごの先端 A が点 P に一致したとすると、 $\angle \mathrm{QBC}$ の大きさはおよそ $\dBox{ス}^{\ \circ}$ になる。

　$\dbox{ス}$ については、最も適当なものを、次の 0 ～ 6 のうちから一つ選べ。

　0: 53
　1: 56
　2: 59
　3: 63
　4: 67
　5: 71
　6: 75

(ii) はしご車に最も近い障害物はフェンスで、フェンスの高さは $7$ m以上あり、障害物の中で最も高いものとする。フェンスは地面に垂直で2点 B, Q の間にあり、フェンスと BQ との交点から点 B までの距離は $6$ mであり。また、フェンスの厚みは考えないとする。

　このとき、次の 0 ～ 6 のフェンスの高さのうち、図３のように、はしごがフェンスに当たらずに、はしごの先端 A を点 P に一致させることができる最大のものは、 $\dBox{セ}$ である。

　$\dbox{セ}$ の解答群

　0: $7$ m
　1: $10$ m
　2: $13$ m
　3: $16$ m
　4: $19$ m
　5: $22$ m
　6: $25$ m

考え方

(1)は難しくないですが、(2)(i)は少し難しいです。工夫して求める必要がありますが、CQ に目が行ってしまうと、思いつきにくくなってしまうでしょう。

【必答問題】
（三角比の表は省略しています）

解答編

問題

　以下の問題を解答するにあたっては、必要に応じて33ページの三角比の表を用いてもよい。

　火災時にビルの高層階に取り残された人を救出する際、はしご車を使用することがある。

　図１のはしご車で考える。はしごの先端を A、はしごの支点を B とする。はしごの角度（はしごと水平面のなす角の大きさ）は $75^{\circ}$ まで大きくすることができ、はしごの長さ AB は $35$ mまで伸ばすことができる。また、はしごの支点 B は地面から $2$ mの高さにあるとする。

　以下、はしごの長さ AB は $35$ mに固定して考える。また、はしごは太さを無視して線分とみなし、はしご車は水平な地面上にあるものとする。

(1) はしごの先端 A の最高到達点の高さは、地面から $\myBox{サシ}$ mである。小数第1位を四捨五入して答えよ。

解説

はしごの角度を $75^{\circ}$ にしたときが一番高くなります。そのため、最高到達点は $(2+35\sin 75^{\circ})$ mとなります。三角比の表を用いて計算すると\[ 2+35\cdot 0.9659=35.8065 \]となるので、 $36$ mとなります。

解答

サシ：36

解答編 つづき

問題

(2) 図１のはしごは、図２のように、点 C で、AC が鉛直方向になるまで下向きに屈折させることができる。AC の長さは $10$ mである。

　図３のように、あるビルにおいて、地面から $26$ mの高さにある位置を点 P とする。障害物のフェンスや木があるため、はしご車を BQ の長さが $18$ mとなる場所にとめる。ここで、点 Q は、点 P の真下で、点 B と同じ高さにある位置である。

　このとき、はしごの先端 A が点 P に届くかどうかは、障害物の高さや、はしご車と障害物の距離によって決まる。そこで、このことについて、後の(i)、(ii)のように考える。

　ただし、はしご車、障害物、ビルは同じ水平な地面上にあり、点 A, B, C, P, Q はすべて同一平面上にあるものとする。

(i) はしごを点 C で屈折させ、はしごの先端 A が点 P に一致したとすると、 $\angle \mathrm{QBC}$ の大きさはおよそ $\dBox{ス}^{\ \circ}$ になる。

　$\dbox{ス}$ については、最も適当なものを、次の 0 ～ 6 のうちから一つ選べ。

　0: 53
　1: 56
　2: 59
　3: 63
　4: 67
　5: 71
　6: 75

解説

図のままだと考えづらいので、座標平面上で考えることにしましょう。点 B から地面に下した垂線と地面との交点を O とし、 $1$ m を 1目盛りとして考えることにします。

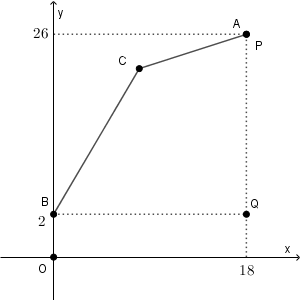
上の図は、わかりやすいように、縮尺を変えています。

上の図で、BQ, PQ と $\angle \mathrm{ Q }$ から、三角形 BPQ の形状が決まります。また、三角形 BCP の三辺の長さがわかるので、この三角形も形状が決まります。そのため、はしごの先端 A が P に一致したとすると、四角形 PCBQ の形状が1つに決まることがわかります。

さて、 $\angle \mathrm{ QBC }$ を求めるには、この角を含む $\triangle \mathrm{ QBC }$ を考えたくなります。しかし、 CQ の長さがわからないため、求めるのは難しいです。そのため、直接求めるのではなく工夫して求めます。

BP で分けて考えます。つまり、\[ \angle \mathrm{ QBC }=\angle \mathrm{ PBQ }+\angle \mathrm{ CBP } \]と分けて考えることにします。

三角形 BPQ は直角三角形であり、 $\tan \angle\mathrm{ PBQ }=\dfrac{24}{18}=\dfrac{4}{3}$ です。三角比の表で、 $\tan$ が $1.3333$ に近い角度を探すと、 $53^{\circ}$ が見つかります。

残りの $\angle \mathrm{ CBP }$ を考えます。三角形 BCP は三辺の長さが決まっているので、余弦定理が使えそうです。 $\mathrm{BQ}:\mathrm{PQ}=18:24=3:4$ なので、 $\mathrm{ BP }=30$ だから
\begin{eqnarray} \cos \angle \mathrm{ CBP } &=& \frac{\mathrm{ CB }^2+\mathrm{ BP }^2-\mathrm{ CP }^2}{2\mathrm{ CB }\cdot \mathrm{ BP } } \\[5pt] &=& \frac{25^2+30^2-10^2}{2\cdot 25\cdot 30} \\[5pt] &=& \frac{5^2+6^2-2^2}{2\cdot 30} \\[5pt] &=& \frac{57}{60} \\[5pt] &=& 0.95 \\[5pt] \end{eqnarray}と求められます。三角比の表から $\cos$ が $0.95$ に近い角を探すと、 $18^{\circ}$ が見つかります。

こうして、$\angle \mathrm{ QBC }$ のおおよその大きさは\[ 53^{\circ}+18^{\circ}=71^{\circ} \]となることがわかります。

解答

ス：5

解答編 つづき

問題

(ii) はしご車に最も近い障害物はフェンスで、フェンスの高さは $7$ m以上あり、障害物の中で最も高いものとする。フェンスは地面に垂直で2点 B, Q の間にあり、フェンスと BQ との交点から点 B までの距離は $6$ mであり。また、フェンスの厚みは考えないとする。

　このとき、次の 0 ～ 6 のフェンスの高さのうち、図３のように、はしごがフェンスに当たらずに、はしごの先端 A を点 P に一致させることができる最大のものは、 $\dBox{セ}$ である。

　$\dbox{セ}$ の解答群

　0: $7$ m
　1: $10$ m
　2: $13$ m
　3: $16$ m
　4: $19$ m
　5: $22$ m
　6: $25$ m

解説

フェンスにギリギリ当たる場合を考えてみます。このときよりもフェンスを低くすれば、フェンスには当たらないことがわかります。

フェンスとはしご車は、水平距離で $6$ m離れているので、ビルとフェンスは水平距離で $12$ m離れています。 AC の長さは $10$ mなので、はしご車とフェンスがギリギリ当たる場合を考えるには、BC とフェンスが当たる場合を考えればいいです。このときの当たる点を D とおきます。

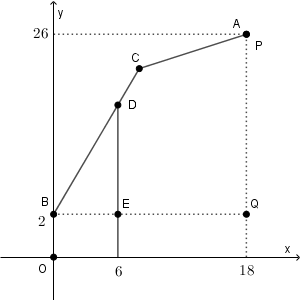
D から地面に引いた垂線と BQ との交点を E とします。このとき、 $\angle \mathrm{ DBE }=\angle \mathrm{ QBC }$ なので、先ほど求めた通り、およそ $71^{\circ}$ だとわかります。よって、DE のおおよその長さは\[ 6\tan71^{\circ}=6\times 2.9042=17.4252 \]と求められます。よって、 D の $y$ 座標は、およそ $19.4252$ なので、はしごが当たらないフェンスの最大の長さは $19$ mと求められます。

解答

セ：4