共通テスト 数学I・数学A 2017年度プレテスト 第1問 [2] 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
以下の問題では、 $\triangle \mathrm{ ABC }$ に対して、 $\angle \mathrm{ A }$, $\angle \mathrm{ B }$, $\angle \mathrm{ C }$ の大きさをそれぞれ A, B, C で表すものとする。
ある日、太郎さんと花子さんのクラスでは、数学の授業で先生から次のような宿題が出された。
【宿題】
$\triangle \mathrm{ ABC }$ において $A=60^{\circ}$ であるとする。このとき、\[ X=4\cos^2 B+4\sin^2C-4\sqrt{3}\cos B\sin C \]の値について調べなさい。放課後、太郎さんと花子さんは出された宿題について会話をした。二人の会話を読んで、下の問いに答えよ。
- A は $60^\circ$ だけど、 B も C もわからないから、方針が立たないよ。
- まずは、具体的に一つ例を作って考えてみようよ。もし $B=90^{\circ}$ であるとすると、 $\cos B = \myBox{オ}$, $\sin C = \myBox{カ}$ だね。だから、この場合の X の値を計算すると $1$ になるね。
(1) $\myBox{オ}$, $\myBox{カ}$ に当てはまるものを、次の 0~8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $0$
1: $1$
2: $-1$3: $\dfrac{1}{2}$
4: $\dfrac{\sqrt{2} }{2}$5: $\dfrac{\sqrt{3} }{2}$
6: $-\dfrac{1}{2}$7: $-\dfrac{\sqrt{2} }{2}$
8: $-\dfrac{\sqrt{3} }{2}$
- $B=13^{\circ}$ にしてみよう。数学の教科書に三角比の表があるから、それを見ると、 $\cos B=0.9744$ で、 $\sin C$ は……あれっ? 表には $0^{\circ}$ から $90^{\circ}$ までの三角比の値しか載っていないから分からないね。
- そういうときは、 $\myBox{キ}$ という関係を利用したらいいよ。この関係を使うと、教科書の三角比の表から $\sin C= \myBox{ク}$ だと分かるよ。
- じゃあ、この場合の X の値を電卓を使って計算してみよう。 $\sqrt{3}$ は $1.732$ として計算すると……あれっ? ぴったりにはならなかったけど、小数第4位を四捨五入すると、 X は $1.000$ になったよ! $_{(\mathrm{ a })}$ これで、 $A=60^{\circ}$, $B=13^{\circ}$ のときに $X=1$ になることが証明できたことになるね。さらに、$_{\mathrm{ (b) } }$ 「 $A=60^{\circ}$ ならば $X=1$ 」という命題が真であると証明できたね。
- 本当にそうなのかな?
(2) $\myBox{キ}$, $\myBox{ク}$ に当てはまる最も適当なものを、次の各解答群のうちから一つずつ選べ。
$\myBox{キ}$ の解答群:
0: $\sin (90^{\circ} -\theta) = \sin \theta$
1: $\sin (90^{\circ} -\theta) =-\sin \theta$
2: $\sin (90^{\circ} -\theta) = \cos \theta$
3: $\sin (90^{\circ} -\theta) =-\cos \theta$
4: $\sin (180^{\circ} -\theta)= \sin \theta$
5: $\sin (180^{\circ} -\theta)=-\sin \theta$
6: $\sin (180^{\circ} -\theta)= \cos \theta$
7: $\sin (180^{\circ} -\theta)=-\cos \theta$$\myBox{ク}$ の解答群:
0: $-3.2709$
1: $-0.9563$
2: $0.9563$
3: $3.2709$(3) 太郎さんが言った下線部 (a), (b) について、その正誤の組合せとして正しいものを、次の 0~3 のうちから一つ選べ。 $\myBox{ケ}$
0: 下線部 (a), (b) ともに正しい。
1: 下線部 (a) は正しいが、(b) は誤りである。
2: 下線部 (a) は誤りであるが、(b) は正しい。
3: 下線部 (a), (b)ともに誤りである。
- $A=60^{\circ}$ ならば $X=1$ となるかどうかを、数式を使って考えてみようよ。 $\triangle \mathrm{ ABC }$ の外接円の半径を R とするね。すると、 $A=60^{\circ}$ だから、 $\mathrm{ BC }=\sqrt{\myBox{コ} }R$ になるね。
- $\mathrm{ AB } = \myBox{サ}$, $\mathrm{ AC } = \myBox{シ}$ になるよ。
(4) $\myBox{コ}$ に当てはまる数を答えよ。また、 $\myBox{サ}$, $\myBox{シ}$ に当てはまるものを、次の 0~7 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $R\sin B$
1: $2R\sin B$
2: $R\cos B$
3: $2R\cos B$
4: $R\sin C$
5: $2R\sin C$
6: $R\cos C$
7: $2R\cos C$
- まず、B が鋭角の場合を考えてみたよ。
【花子さんのノート】
点 C から直線 AB に垂線 CH を引くと
$\mathrm{ AH } = \underline{\mathrm{ AC }\cos 60^{\circ} } _{①}$
$\mathrm{ BH } = \underline{\mathrm{ BC }\cos B} _{②}$
である。 AB を AH, BH を用いて表すと
$\mathrm{ AB } = \underline{\mathrm{ AH }+\mathrm{ BH } } _{③}$
であるから\[\underline{\mathrm{ AB } = \myBox{ス}\sin B+\myBox{セ}\cos B} _{④}\]が得られる。
- さっき、 $\mathrm{ AB } =\myBox{サ}$ と求めたから、 ④の式とあわせると、 $X=1$ となることが証明できたよ。
- B が直角のときは、すでに $X=1$ となることを計算したね。 $_{(\mathrm{ c })}$ B が鈍角のときは、証明を少し変えれば、やはり $X=1$ であることが示せるね。
(5) $\myBox{ス}$, $\myBox{セ}$ に当てはまるものを、次の 0~8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $\dfrac{1}{2}R$
1: $\dfrac{\sqrt{2} }{2}R$2: $\dfrac{\sqrt{3} }{2}R$
3: $R$
4: $\sqrt{2}R$
5: $\sqrt{3}R$6: $2R$
7: $2\sqrt{2}R$
8: $2\sqrt{3}R$(6) 下線部 (c) について、 B が鈍角のときには下線部①~③の式のうち修正が必要なものがある。修正が必要な番号についてのみ、修正した式をそれぞれ答えよ。解答は、解答欄 $\myBox{(い)}$ に記述せよ。
- 今まではずっと $A=60^{\circ}$ の場合を考えてきたんだけど、 $A=120^{\circ}$ で $B=30^{\circ}$ の場合を考えてみたよ。 $\sin B$ と $\cos C$ の値を求めて、 X の値を計算したら、この場合にも $1$ になったんだよね。
- わっ、本当だ。計算してみたら X の値は $1$ になるね。
(7) $\triangle \mathrm{ ABC }$ について、次の条件 p, q を考える。
\begin{eqnarray} p&:&\ A=60^{\circ} \\[5pt] q&:&\ 4\cos^2 B+4\sin^2 C -4\sqrt{3}\cos B \sin C =1 \end{eqnarray}これまでの太郎さんと花子さんが行った考察をもとに、正しいと判断できるものを、次の 0~3 のうちから一つ選べ。 $\myBox{ソ}$
0: p は q であるための必要十分条件である。
1: p は q であるための必要条件であるが、十分条件でない。
2: p は q であるための十分条件であるが、必要条件でない。
3: p は q であるための必要条件でも十分条件でもない。
考え方
三角比の内容に、ところどころ命題の内容が混じっている問題です。
文章が長いですが、難しいことはあまりやっていません。ただ、条件が問題によって変わるので、「今考えている問題では、何が仮定されているか」をよく確かめながら考えていきましょう。
センター試験に比べて計算問題はほとんどありません。記述も、図が描ければすぐにわかる内容です。
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
解答編
問題
以下の問題では、 $\triangle \mathrm{ ABC }$ に対して、 $\angle \mathrm{ A }$, $\angle \mathrm{ B }$, $\angle \mathrm{ C }$ の大きさをそれぞれ A, B, C で表すものとする。
ある日、太郎さんと花子さんのクラスでは、数学の授業で先生から次のような宿題が出された。
【宿題】
$\triangle \mathrm{ ABC }$ において $A=60^{\circ}$ であるとする。このとき、\[ X=4\cos^2 B+4\sin^2C-4\sqrt{3}\cos B\sin C \]の値について調べなさい。放課後、太郎さんと花子さんは出された宿題について会話をした。二人の会話を読んで、下の問いに答えよ。
- A は $60^\circ$ だけど、 B も C もわからないから、方針が立たないよ。
- まずは、具体的に一つ例を作って考えてみようよ。もし $B=90^{\circ}$ であるとすると、 $\cos B = \myBox{オ}$, $\sin C = \myBox{カ}$ だね。だから、この場合の X の値を計算すると $1$ になるね。
(1) $\myBox{オ}$, $\myBox{カ}$ に当てはまるものを、次の 0~8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $0$
1: $1$
2: $-1$3: $\dfrac{1}{2}$
4: $\dfrac{\sqrt{2} }{2}$5: $\dfrac{\sqrt{3} }{2}$
6: $-\dfrac{1}{2}$7: $-\dfrac{\sqrt{2} }{2}$
8: $-\dfrac{\sqrt{3} }{2}$
解説
これはサービス問題です。
$B=90^{\circ}$ なので、 $\cos B=0$ ですね。 $A=60^{\circ}$ なので、 $C=30^{\circ}$ です。よって、 $\sin C=\dfrac{1}{2}$ となります。
ちなみに、 X の値を計算してみましょう。(計算しなくても問題ありませんが)
\begin{eqnarray}
X
&=&
4\cos^2 B+4\sin^2C-4\sqrt{3}\cos B\sin C \\[5pt]
&=&
0 + 4\times \left(\dfrac{1}{2}\right)^2 -0 \\[5pt]
&=&
1
\end{eqnarray}となり、確かに $X=1$ となっていますね。
解答
オ:0
カ:3
参考
解答編 つづき
問題
- $B=13^{\circ}$ にしてみよう。数学の教科書に三角比の表があるから、それを見ると、 $\cos B=0.9744$ で、 $\sin C$ は……あれっ? 表には $0^{\circ}$ から $90^{\circ}$ までの三角比の値しか載っていないから分からないね。
- そういうときは、 $\myBox{キ}$ という関係を利用したらいいよ。この関係を使うと、教科書の三角比の表から $\sin C= \myBox{ク}$ だと分かるよ。
- じゃあ、この場合の X の値を電卓を使って計算してみよう。 $\sqrt{3}$ は $1.732$ として計算すると……あれっ? ぴったりにはならなかったけど、小数第4位を四捨五入すると、 X は $1.000$ になったよ! $_{(\mathrm{ a })}$ これで、 $A=60^{\circ}$, $B=13^{\circ}$ のときに $X=1$ になることが証明できたことになるね。さらに、$_{\mathrm{ (b) } }$ 「 $A=60^{\circ}$ ならば $X=1$ 」という命題が真であると証明できたね。
- 本当にそうなのかな?
(2) $\myBox{キ}$, $\myBox{ク}$ に当てはまる最も適当なものを、次の各解答群のうちから一つずつ選べ。
$\myBox{キ}$ の解答群:
0: $\sin (90^{\circ} -\theta) = \sin \theta$
1: $\sin (90^{\circ} -\theta) =-\sin \theta$
2: $\sin (90^{\circ} -\theta) = \cos \theta$
3: $\sin (90^{\circ} -\theta) =-\cos \theta$
4: $\sin (180^{\circ} -\theta)= \sin \theta$
5: $\sin (180^{\circ} -\theta)=-\sin \theta$
6: $\sin (180^{\circ} -\theta)= \cos \theta$
7: $\sin (180^{\circ} -\theta)=-\cos \theta$$\myBox{ク}$ の解答群:
0: $-3.2709$
1: $-0.9563$
2: $0.9563$
3: $3.2709$(3) 太郎さんが言った下線部 (a), (b) について、その正誤の組合せとして正しいものを、次の 0~3 のうちから一つ選べ。 $\myBox{ケ}$
0: 下線部 (a), (b) ともに正しい。
1: 下線部 (a) は正しいが、(b) は誤りである。
2: 下線部 (a) は誤りであるが、(b) は正しい。
3: 下線部 (a), (b)ともに誤りである。
解説
$A=60^{\circ}$, $B=13^{\circ}$ なので、 $C=107^{\circ}$ となります。三角比の表には、 $90^{\circ}$ までしか載っていないので、 $90^{\circ}$ 以下に変換できるような関係式が必要ですね。なので、 $180^{\circ}-\theta$ を用いた関係式を用います。 $\theta=73^{\circ}$ とすれば、 $107^{\circ}$ の三角比を $90^{\circ}$ 以下の角を使った三角比で表すことができるので、三角比の表が使えるようになります。
$\sin$ は、単位円で考えると y 座標なので、 $\sin \theta$ も $\sin (180^{\circ}-\theta)$ も同じ値になります。よって、クは、選択肢 4 が正解となります。
$0^{\circ} \lt \theta \lt 180^{\circ}$ のときは、 $\sin \theta$ の値は正で $1$ 以下なので、クに当てはまるものは、選択肢 2しかありません。
続いて、下線部の正誤について考えます。
(a) の直前で「小数第4位を四捨五入すれば $X=1.000$ になった」と言っていますが、数学の世界では、これが $X=1$ の証明になるわけがありません。厳密に $1$ と一致しない限り、 $X=1$ の証明にはなりません。
また、 $B=13^{\circ}$ の場合しか考えていないのだから、それ以外の角度の場合も含んでいる (b) が証明できることはありえません。
つまり、下線部(a)(b)は、どちらも間違いです。
解答
キ:4ク:2
ケ:3
参考
解答編 つづき
問題
- $A=60^{\circ}$ ならば $X=1$ となるかどうかを、数式を使って考えてみようよ。 $\triangle \mathrm{ ABC }$ の外接円の半径を R とするね。すると、 $A=60^{\circ}$ だから、 $\mathrm{ BC }=\sqrt{\myBox{コ} }R$ になるね。
- $\mathrm{ AB } = \myBox{サ}$, $\mathrm{ AC } = \myBox{シ}$ になるよ。
(4) $\myBox{コ}$ に当てはまる数を答えよ。また、 $\myBox{サ}$, $\myBox{シ}$ に当てはまるものを、次の 0~7 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $R\sin B$
1: $2R\sin B$
2: $R\cos B$
3: $2R\cos B$
4: $R\sin C$
5: $2R\sin C$
6: $R\cos C$
7: $2R\cos C$
解説
三角比のところで外接円が出てきたら、正弦定理を使うと予想できます。
正弦定理より
\begin{eqnarray}
\mathrm{ BC }
&=&
2R\sin A \\[5pt]
&=&
2R\sin 60^{\circ} \\[5pt]
&=&
\sqrt{3}R \\[5pt]
\end{eqnarray}となります。
また、同様に、正弦定理から
\begin{eqnarray}
\mathrm{ AB }=2R\sin C, \mathrm{ AC }=2R\sin B
\end{eqnarray}が得られます。特にひねりはありません。
解答
コ:3サ:5
シ:1
参考
解答編 つづき
問題
- まず、B が鋭角の場合を考えてみたよ。
【花子さんのノート】
点 C から直線 AB に垂線 CH を引くと
$\mathrm{ AH } = \underline{\mathrm{ AC }\cos 60^{\circ} } _{①}$
$\mathrm{ BH } = \underline{\mathrm{ BC }\cos B} _{②}$
である。 AB を AH, BH を用いて表すと
$\mathrm{ AB } = \underline{\mathrm{ AH }+\mathrm{ BH } } _{③}$
であるから\[\underline{\mathrm{ AB } = \myBox{ス}\sin B+\myBox{セ}\cos B} _{④}\]が得られる。
- さっき、 $\mathrm{ AB } =\myBox{サ}$ と求めたから、 ④の式とあわせると、 $X=1$ となることが証明できたよ。
- B が直角のときは、すでに $X=1$ となることを計算したね。 $_{(\mathrm{ c })}$ B が鈍角のときは、証明を少し変えれば、やはり $X=1$ であることが示せるね。
(5) $\myBox{ス}$, $\myBox{セ}$ に当てはまるものを、次の 0~8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $\dfrac{1}{2}R$
1: $\dfrac{\sqrt{2} }{2}R$2: $\dfrac{\sqrt{3} }{2}R$
3: $R$
4: $\sqrt{2}R$
5: $\sqrt{3}R$6: $2R$
7: $2\sqrt{2}R$
8: $2\sqrt{3}R$(6) 下線部 (c) について、 B が鈍角のときには下線部①~③の式のうち修正が必要なものがある。修正が必要な番号についてのみ、修正した式をそれぞれ答えよ。解答は、解答欄 $\myBox{(い)}$ に記述せよ。
解説
ノートの通りに計算していくと
\begin{eqnarray}
\mathrm{ AB }
&=&
\mathrm{ AH }+\mathrm{ BH } \\[5pt]
&=&
\mathrm{ AC } \cos 60^{\circ}+\mathrm{ BC } \cos B \\[5pt]
\end{eqnarray}となります。ここに、コサシの結果(正弦定理を用いたところ)を代入すると
\begin{eqnarray}
\mathrm{ AB }
&=&
2R\sin B \times \frac{1}{2}+\sqrt{3}R\times \cos B \\[5pt]
&=&
R\sin B +\sqrt{3}R\cos B \\[5pt]
\end{eqnarray}となります。
また、鈍角のときは次のような図になります。
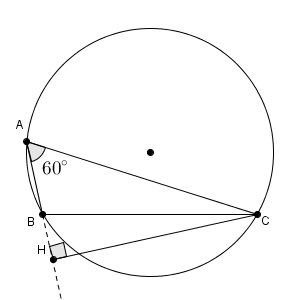
$\mathrm{ AH }=\mathrm{ AC }\cos 60^{\circ}$ は変わりませんが、 BH は角を変えないといけません。 $\angle \mathrm{ ABC }$ ではなく、 $\angle \mathrm{ HBC }$ を使わなければならず、 $\mathrm{ BH }=\mathrm{ BC }\cos (180^{\circ}-B)$ となります。また、図から、 $\mathrm{ AB }=\mathrm{ AH }-\mathrm{ BH }$ となることがわかります。
解答
ス:3
セ:5
(い)
①:(変更なし)
②: $\mathrm{ BC }\cos (180^{\circ}-B)$
③: $\mathrm{ AH }-\mathrm{ BH }$
解答編 つづき
問題
- 今まではずっと $A=60^{\circ}$ の場合を考えてきたんだけど、 $A=120^{\circ}$ で $B=30^{\circ}$ の場合を考えてみたよ。 $\sin B$ と $\cos C$ の値を求めて、 X の値を計算したら、この場合にも $1$ になったんだよね。
- わっ、本当だ。計算してみたら X の値は $1$ になるね。
(7) $\triangle \mathrm{ ABC }$ について、次の条件 p, q を考える。
\begin{eqnarray} p&:&\ A=60^{\circ} \\[5pt] q&:&\ 4\cos^2 B+4\sin^2 C -4\sqrt{3}\cos B \sin C =1 \end{eqnarray}これまでの太郎さんと花子さんが行った考察をもとに、正しいと判断できるものを、次の 0~3 のうちから一つ選べ。 $\myBox{ソ}$
0: p は q であるための必要十分条件である。
1: p は q であるための必要条件であるが、十分条件でない。
2: p は q であるための十分条件であるが、必要条件でない。
3: p は q であるための必要条件でも十分条件でもない。
解説
今まで考えてきた内容から、 p ならば q が成り立ちます。また、(7)の直近の記述から、 q ならば p は成り立たないことがわかります。
以上から、 p は q であるための十分条件であるが、必要条件でないことがわかります。
解答
ソ:2





