共通テスト 数学I・数学A 2017年度プレテスト 第2問 [2] 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
地方の経済活性化のため、太郎さんと花子さんは観光客の消費に着目し、その拡大に向けて基礎的な情報を整理することにした。以下は、都道府県別の統計データを集め、分析しているときの二人の会話である。会話を読んで下の問いに答えよ。ただし、東京都、大阪府、福井県の3都府県のデータは含まれていない。また、以後の問題文では「道府県」を単に「県」として表記する。
- 各県を訪れた観光客数を x 軸、消費総額を y 軸にとり、散布図をつくると図1のようになったよ。
- 消費総額を観光客数で割った消費額単価が最も高いのはどこかな。
- 元のデータを使って県ごとに割り算をすれば分かるよ。北海道は……。44回も計算するのは大変だし、間違えそうだな。
- 図1を使えばすぐ分かるよ。
(1) 図1の観光客数と消費総額の間の相関係数に最も近い値を、次の 0~4 のうちから一つ選べ。 $\myBox{シ}$
0: -0.85
1: -0.52
2: 0.02
3: 0.34
4: 0.83(2) 44県それぞれの消費額単価を計算しなくても、図1の散布図から消費額単価が最も高い県を表す点を特定することができる。その方法を、「直線」という単語を用いて説明せよ。解答は、解答欄 $\myBox{(う)}$ に記述せよ。
(3) 消費額単価が最も高い県を表す点を、図1の 0~9 のうちから一つ選べ。 $\myBox{ス}$
- 元のデータを見ると消費額単価が最も高いのは沖縄県だね。沖縄県の消費額単価が高いのは、県外からの観光客数の影響かな。
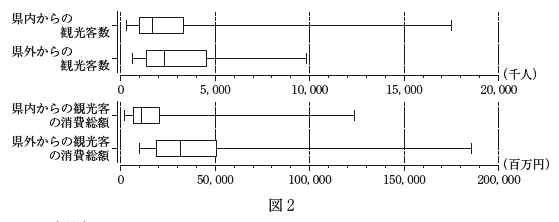
- 県内からの観光客と県外からの観光客とに分けて44県の観光客数と消費総額を箱ひげ図で表すと図2のようになったよ。
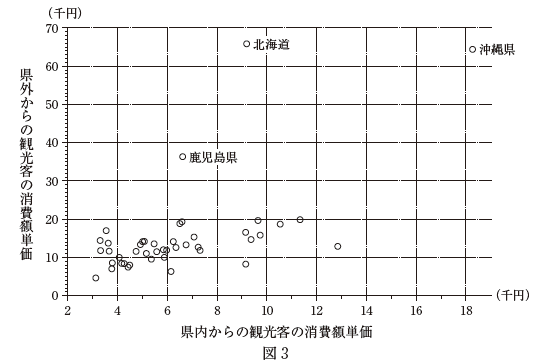
- 私は県内と県外からの観光客の消費額単価をそれぞれ横軸と縦軸にとって図3の散布図をつくってみたよ。沖縄県は県内、県外ともに観光客の消費額単価は高いね。それに、北海道、鹿児島県、沖縄県は全体の傾向から外れているみたい。
(4) 図2、図3から読み取れる事柄として正しいものを、次の 0~4 のうちから二つ選べ。 $\myBox{セ}$
0: 44県の半分の県では、県内からの観光客数よりも県外からの観光客数の方が多い。
1: 44県の半分の県では、県内からの観光客の消費総額よりも県外からの観光客の消費総額の方が高い。
2: 44県の4分の3以上の県では、県外からの観光客の消費額単価の方が県内からの観光客の消費額単価より高い。
3: 県外からの観光客の消費額単価の平均値は、北海道、鹿児島県、沖縄県を除いた41県の平均値の方が44県の平均値より小さい。
4: 北海道、鹿児島県、沖縄県を除いて考えると、県内からの観光客の消費額単価の分散よりも県外からの観光客の消費額単価の分散の方が小さい。
(5) 二人は県外からの観光客に焦点を絞って考えることにした。
- 県外からの観光客数を増やすには、イベントなどを増やしたらいいんじゃないかな。
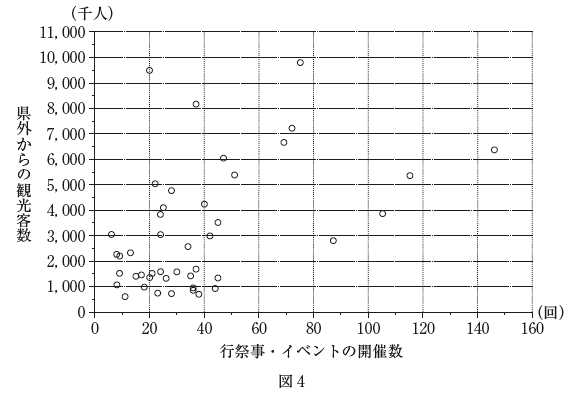
- 44県の行祭事・イベントの開催数と県外からの観光客数を散布図にすると、図4のようになったよ。
図4から読み取れることとして最も適切な記述を、次の 0~4 のうちから一つ選べ。 $\myBox{ソ}$
0: 44県の行祭事・イベント開催数の中央値は、その平均値よりも大きい。
1: 行祭事・イベントを多く開催し過ぎると、県外からの観光客数は減ってしまう傾向がある。
2: 県外からの観光客数を増やすには行祭事・イベントの開催数を増やせばよい。
3: 行祭事・イベントの開催数が最も多い県では、行祭事・イベントの開催一回当たりの県外からの観光客数は6,000千人を超えている。
4: 県外からの観光客数が多い県ほど、行祭事・イベントを多く開催している傾向がある。
(本問題の図は、「共通基準による観光入込客統計」(観光庁)をもとにして作成している。)
考え方
データの分析に関する問題です。
問題文や図について、細かいところまで見て解くようにしましょう。見落としがあると、間違った選択肢を選んでしまう可能性があります。
後半は、選択肢を1つ1つ吟味しなければいけないので、時間がかかりますが、落ち着いて考えていきましょう。
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
解答編
問題
地方の経済活性化のため、太郎さんと花子さんは観光客の消費に着目し、その拡大に向けて基礎的な情報を整理することにした。以下は、都道府県別の統計データを集め、分析しているときの二人の会話である。会話を読んで下の問いに答えよ。ただし、東京都、大阪府、福井県の3都府県のデータは含まれていない。また、以後の問題文では「道府県」を単に「県」として表記する。
- 各県を訪れた観光客数を x 軸、消費総額を y 軸にとり、散布図をつくると図1のようになったよ。
- 消費総額を観光客数で割った消費額単価が最も高いのはどこかな。
- 元のデータを使って県ごとに割り算をすれば分かるよ。北海道は……。44回も計算するのは大変だし、間違えそうだな。
- 図1を使えばすぐ分かるよ。
(1) 図1の観光客数と消費総額の間の相関係数に最も近い値を、次の 0~4 のうちから一つ選べ。 $\myBox{シ}$
0: -0.85
1: -0.52
2: 0.02
3: 0.34
4: 0.83
解説
散布図を見ると、左下に点が集中していて、右上の方にもいくつか点があります。よって、正の相関関係があることがわかります。
また、左上や右下には点がほとんどなく、右上がりの直線から外れている点が少ないため、相関係数は1に近い値になることがわかります。
以上から、選択肢の中で一番近いと考えられるものは4の 0.83 だとわかります。
解答
シ:4
参考
解答編 つづき
問題
(2) 44県それぞれの消費額単価を計算しなくても、図1の散布図から消費額単価が最も高い県を表す点を特定することができる。その方法を、「直線」という単語を用いて説明せよ。解答は、解答欄 $\myBox{(う)}$ に記述せよ。
(3) 消費額単価が最も高い県を表す点を、図1の 0~9 のうちから一つ選べ。 $\myBox{ス}$
解説
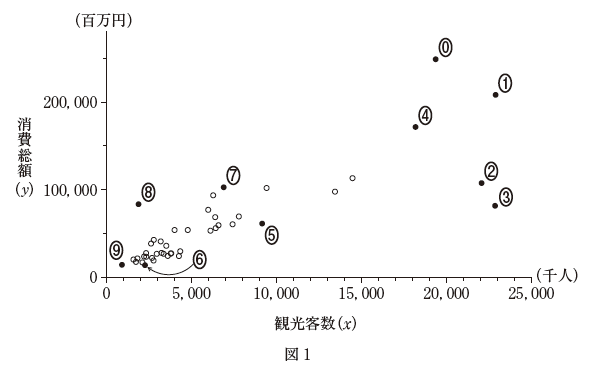
消費額単価は、消費総額を観光客数で割ったものなのです。なので、消費額単価は、各点に対して、原点とを結んだ直線の傾きに対応します。この傾きが一番大きいものが、消費額単価が最も高いものだ、と特定できます。
上の散布図で言うと、8番が該当することがわかります。
解答
(う)
各点に対して、その点と原点とを結んだ直線を引き、傾きが一番大きくなるような点を選ぶ。
ス:8
解答編 つづき
問題
- 元のデータを見ると消費額単価が最も高いのは沖縄県だね。沖縄県の消費額単価が高いのは、県外からの観光客数の影響かな。
- 県内からの観光客と県外からの観光客とに分けて44県の観光客数と消費総額を箱ひげ図で表すと図2のようになったよ。
- 私は県内と県外からの観光客の消費額単価をそれぞれ横軸と縦軸にとって図3の散布図をつくってみたよ。沖縄県は県内、県外ともに観光客の消費額単価は高いね。それに、北海道、鹿児島県、沖縄県は全体の傾向から外れているみたい。
(4) 図2、図3から読み取れる事柄として正しいものを、次の 0~4 のうちから二つ選べ。 $\myBox{セ}$
0: 44県の半分の県では、県内からの観光客数よりも県外からの観光客数の方が多い。
1: 44県の半分の県では、県内からの観光客の消費総額よりも県外からの観光客の消費総額の方が高い。
2: 44県の4分の3以上の県では、県外からの観光客の消費額単価の方が県内からの観光客の消費額単価より高い。
3: 県外からの観光客の消費額単価の平均値は、北海道、鹿児島県、沖縄県を除いた41県の平均値の方が44県の平均値より小さい。
4: 北海道、鹿児島県、沖縄県を除いて考えると、県内からの観光客の消費額単価の分散よりも県外からの観光客の消費額単価の分散の方が小さい。
解説
1つ1つ見ていくしかありません。
選択肢0は、各県の「県内の観光客数と県外の観光客数」を表す図がないので、そもそも読み取ることができません。図2の1つ目の箱ひげ図からは、各県に関する情報は読み取れません。なのでこれは不適です。
選択肢1も、同様です。各県の「県内からの観光客の消費総額と県外からの観光客の消費総額」を表す図はないので、不適です。
選択肢2は、図3が使えます。消費額単価を比べてみましょう。縦軸と横軸の目盛りが異なることに注意が必要です。10千円同士の点と原点とを結ぶ直線を引きます。その直線より上に点があれば「県外の方が高い」、下にあれば「県内の方が高い」といえます。ほとんどすべての点で「県外の方が高い」が言えますね。下にある点は10個もないです。なので、これは正しいです。
選択肢3は、3つの県の情報が載っている図3を使います。県外からの観光客の消費額単価は、縦について見ればいいですね。北海道、鹿児島県、沖縄県は、どれも他の県よりも単価が高いですね。なので、この3県を除いて平均をとれば、除かないときより値は小さくなります。これも正しいです。
選択肢4も、3つの県の情報が載っている図3を使います。北海道、鹿児島県、沖縄県を除いた41県について、消費額単価を比べるのですね。パッと見ると、縦方向にすごくかたまっているので、県外の方が分散が小さいように見えます。しかし、縦軸と横軸では、目盛りが違うことに注意しましょう。県内は、3~13千円の範囲で散らばっていて、県外は5~20千円あたりの範囲で散らばっています。図3だけでは判断することは難しいでしょう。
以上から、選択肢2, 3が正しいと考えられます。
解答
セ:2, 3
解答編 つづき
問題
(5) 二人は県外からの観光客に焦点を絞って考えることにした。
- 県外からの観光客数を増やすには、イベントなどを増やしたらいいんじゃないかな。
- 44県の行祭事・イベントの開催数と県外からの観光客数を散布図にすると、図4のようになったよ。
図4から読み取れることとして最も適切な記述を、次の 0~4 のうちから一つ選べ。 $\myBox{ソ}$
0: 44県の行祭事・イベント開催数の中央値は、その平均値よりも大きい。
1: 行祭事・イベントを多く開催し過ぎると、県外からの観光客数は減ってしまう傾向がある。
2: 県外からの観光客数を増やすには行祭事・イベントの開催数を増やせばよい。
3: 行祭事・イベントの開催数が最も多い県では、行祭事・イベントの開催一回当たりの県外からの観光客数は6,000千人を超えている。
4: 県外からの観光客数が多い県ほど、行祭事・イベントを多く開催している傾向がある。
(本問題の図は、「共通基準による観光入込客統計」(観光庁)をもとにして作成している。)
解説
一つずつ確認していきましょう。
選択肢0は、図4の横軸についてです。一般に、大きすぎる値がいくつかあると、それらの値に引っ張られて平均値が大きくなり、中央値のほうが小さくなります。なので、0は適切ではありません。
選択肢1は、図で、右に行き過ぎると下に行く、となってないといけませんが、そんなことにはなっていません。なので適切ではありません。
選択肢2は、難しいですね。図を見ると、「県外からの観光客数と行祭事・イベントの開催数」には正の相関があることがわかります。しかし、だからと言って、「行祭事・イベントの開催数を増やせば、県外からの観光客数が増える」とは限りません。実際には増えるのかもしれませんが、断定はできません。
選択肢3について考えましょう。「行祭事・イベントの開催数が最も多い県」とは、図の一番右にある点が対応します。この点は、県外からの観光客数は 6,000千人を超えていますが、選択肢には「行祭事・イベントの開催一回当たり」となっています。合計ではないことに注意です。ここを読み落としてはいけません。この選択肢は適切ではありません。
選択肢4は、「傾向がある」としか言ってません。確かに、正の相関があり、「県外からの観光客数が多い県ほど、行祭事・イベントを多く開催している傾向がある」と言えます。これが最も適切です。選択肢2は、予想が含まれており、少し飛躍があります。
解答
ソ:4