京都大学 理系 2014年度 第5問 解説
問題編
問題
自然数 a, b はどちらも3で割り切れないが、 $a^3+b^3$ は81で割り切れる。このような a, b の組 $(a,b)$ のうち、 $a^2+b^2$ の値を最小にするものと、そのときの $a^2+b^2$ の値を求めよ。
考え方
「3で割り切れないなら、3で割った余りはどうなるんだろう」「81で割り切れるためには、どういう条件が必要だろう」といったところから攻めていきましょう。「割り切れる」という条件なので、 $a^3+b^3$ を因数分解したり、掛け算を使った式変形をして、 a, b に関する条件を絞っていきましょう。
$a+b$ に関する条件が導ければ、あとは二次関数の最小値を求める問題です。
解答編
問題
自然数 a, b はどちらも3で割り切れないが、 $a^3+b^3$ は81で割り切れる。このような a, b の組 $(a,b)$ のうち、 $a^2+b^2$ の値を最小にするものと、そのときの $a^2+b^2$ の値を求めよ。
解答
一般に、
\begin{eqnarray}
& &
(3x+y)^3 \\
&=&
27x^3+27x^2y+9xy^2+y^3 \\
&=&
3(9x^3+9x^2y+3xy^2)+y^3 \\
\end{eqnarray}が成り立つ。このことから、3で割り切れない2つの自然数 a, b に対し、 $a^3+b^3$ が3の倍数になるなら、3で割った余りの3乗同士の和も3の倍数になるため、3で割った余りは片方が1でもう片方が2となる。
以下では、 a, b を $3m+1$, $3n+2$ で表す(m, n は0以上の整数)。
\begin{eqnarray} a^3+b^3 &=& (a+b)(a^2-ab+b^2) \\[5pt] &=& (3m+1+3n+2) \\ & & \times \{ (3m+1)^2-(3m+1)(3n+2)+(3n+2)^2 \} \\[5pt] &=& 3(m+n+1) \\ & & \times ( 9m^2+6m+1-9mn-6m-3n-2 +9n^2+12n+4 ) \\[5pt] &=& 3(m+n+1) ( 9m^2-9mn +9n^2+9n+3 ) \\[5pt] &=& 9(m+n+1) \{ 3(m^2-mn +n^2+n) +1 \} \\ \end{eqnarray}と変形できる。最後の波かっこの中は3の倍数ではないので、 $a^3+b^3$ が81で割り切れるなら、 $m+n+1$ は9の倍数となる。 $a+b=3m+3n+3$ なので、このとき $a+b$ は27の倍数となる。$a+b=27$ とすると
\begin{eqnarray}
a^2+b^2
&=&
a^2+(27-a)^2 \\
&=&
2a^2 -54a +729 \\
&=&
2\left( a -\frac{27}{2} \right)^2 +\frac{729}{2} \\
\end{eqnarray}となる。
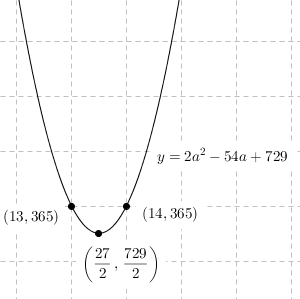
a は自然数なので、 $a^2+b^2$ は $a=13,14$ のときに最小となる。このとき、 a, b は片方が13でもう片方が14なので与えられた条件を満たし、\[ a^2+b^2 = 13^2+14^2=365 \]となる。
また、 $a+b$ が54以上のときは、 a, b のどちらかは27以上となるので\[ a^2+b^2 \gt 27^2 \gt 365 \]となる。
以上から、 $a^2+b^2$ が最小になるのは $(a,b)=(13,14),(14,13)$ のときで、そのときの $a^2+b^2$ は $365$ となる。
(終)
解説
倍数に関する問題なので、 $a^3+b^3$ を因数分解して考えてみましょう。上では、a, b を3で割った余りに注目し、それを使って式変形しているので少し複雑に見えますが、頑張って計算すればあまりひらめきは必要ありません。もう少しスッキリ書くなら次のようにしてもいいでしょう。
<$a+b$ が27の倍数であること、について>
$a-1, a, a+1$ の中には必ず3の倍数が含まれるので\[ (a-1)a(a+1) = a^3-a \]は3の倍数。同様に、 $b^3-b$ も3の倍数なので、\[ a^3-a+b^3-b=(a^3+b^3)-(a+b) \]は3の倍数。 $a^3+b^3$ は3で割り切れるから $a+b$ も3で割り切れる。
<終>
すっきりですが、式変形を思いつくのは少し難しいかもしれません。
$a+b$ が27の倍数であることがわかれば、27のときが一番小さくなるだろうというのは予想できるでしょう。まずは27のときに最小値を求め、27より大きいときにはその最小値を上回ってしまうことを言う方が書きやすいと思います。





