京都大学 理系 2014年度 第4問 解説
問題編
問題
実数の定数 a, b に対して、関数 $f(x)$ を\[ f(x)=\frac{ax+b}{x^2+x+1} \]で定める。すべての実数 x で不等式\[ f(x)\leqq f(x)^3-2f(x)^2+2 \]が成り立つような点 $(a,b)$ の範囲を図示せよ。
考え方
$f(x)$ の式を不等式に代入すると大変なことになります。ここでは、逆に、不等式から $f(x)$ に関する条件を求めて、それを満たす a, b の条件を求める、という方針で解きましょう。
「すべての実数」と「または」がどうつながっているか、注意しながら条件を考えていきましょう。
解答編
問題
実数の定数 a, b に対して、関数 $f(x)$ を\[ f(x)=\frac{ax+b}{x^2+x+1} \]で定める。すべての実数 x で不等式\[ f(x)\leqq f(x)^3-2f(x)^2+2 \]が成り立つような点 $(a,b)$ の範囲を図示せよ。
解答
$y=f(x)$ とすると、与えられた不等式は
\begin{eqnarray}
& & y \leqq y^3 -2y^2+2 \\
& & y^3 -2y^2 -y +2 \geqq 0 \\
& & (y-1)(y^2-y-2) \geqq 0 \\
& & (y-1)(y-2)(y+1) \geqq 0 \\
\end{eqnarray}と変形できるので、「 $-1\leqq y \leqq 1$ または $2\leqq y$ 」と同値である。
ここで、 $\displaystyle x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\gt 0$ だから $y=f(x)$ は連続関数であり、\[ \lim_{x\to\infty} f(x)=\lim_{x\to -\infty} f(x)=0 \]である。もし $2\leqq f(x)$ を満たす x があれば、中間値の定理から $1\lt f(x) \lt 2$ となる x も存在してしまうことになり、このときは与えられた不等式が成り立たない。よって、すべての実数 x で与えられた不等式が成り立つとき、 $2\leqq f(x)$ を満たす x は存在しない。
このことから、すべての実数 x で与えられた不等式が成り立つことは、「すべての実数 x に対して $-1\leqq f(x) \leqq 1$ が成り立つこと」と同値である。
\begin{eqnarray} f(x) & \leqq & 1 \\ ax+b & \leqq & x^2+x+1 \\ x^2+(-a+1)x+(-b+1) & \geqq & 0 \\ \end{eqnarray}がすべての実数で成り立つのは、左辺の判別式が0以下のときなので \begin{eqnarray} (-a+1)^2-4(-b+1) & \leqq & 0 \\[5pt] (a-1)^2-4 & \leqq & -4b \\[5pt] b & \leqq & -\frac{1}{4}(a-1)^2+1 \\[5pt] \end{eqnarray}のとき、となる。
以上から、求める範囲は、2つの領域
\begin{eqnarray}
b & \geqq & \frac{1}{4}(a+1)^2 -1 \\[5pt]
b & \leqq & -\frac{1}{4}(a-1)^2 +1
\end{eqnarray}の共通部分である。ここで、
\begin{eqnarray}
\frac{1}{4}(a+1)^2 -1 &=& -\frac{1}{4}(a-1)^2 +1 \\[5pt]
a^2+2a-3 &=& -a^2+2a+3 \\[5pt]
a &=& \pm\sqrt{3} \\[5pt]
\end{eqnarray}なので、図示すると、次の色のついた部分(境界線上の点を含む)となる。
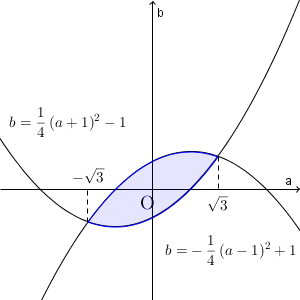
(終)
解説
冒頭の部分について。細かくて少しわかりにくいですが
「すべての x に対して、 $-1\leqq y \leqq 1$ または $2\leqq y$ が成り立つ」
と
「すべての x に対して $-1\leqq y \leqq 1$ が成り立つ、または、すべての x に対して $2\leqq y$ が成り立つ」
は違います。前者は、例えば「 $x=0$ のときは $-1\leqq y \leqq 1$ が成り立ち、 $x=1$ のときは $2\leqq y$ が成り立つ」のような場合もOKですが、後者はダメです。この2つの条件は異なります。
与えられた不等式を変形しただけで得られる条件は前者なので、この例のように「ある箇所では $-1\leqq y \leqq 1$ が成り立って、別の箇所では $2\leqq y$ が成り立つ」ケースもありえるのですが、今考えている状況ではこういうことは起きません。 $2\leqq y$ が成り立つ箇所があると、与えられた不等式が成り立たない部分が出てくるから、 $2\leqq y$ となることはない、というのを書いているのが冒頭の部分です。
ここをきちんとかかずに、「すべての x について $f(x)\geqq 2$ を満たすような a, b はない」などとしか書いていない場合は、上にかいた2つの文章の違いが分かっていないと判断され、大きく減点されることになってしまいます。





