京都大学 文系 2021年度 第1問 解説
問題編
問題
次の各問に答えよ。
問1 10進法で表された数 $6.75$ を2進法で表せ。また、この数と2進法で表された数 $101.0101$ との積として与えられる数を2進法および4進法で表せ。
問2 $\triangle \mathrm{ OAB }$ において $\mathrm{ OA }=3$, $\mathrm{ OB }=2$, $\angle \mathrm{ AOB }=60^{\circ}$ とする。 $\triangle \mathrm{ OAB }$ の垂心を $\mathrm{ H }$ とするとき、 $\overrightarrow{ \mathrm{ OH } }$ を $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OB } }$ を用いて表せ。
考え方
第1問目ということで、計算問題とよく見かける感じベクトルの問題となっています。見かけは簡単そうですが、方針を間違うと時間をロスしてしまうかもしれません。
問1は、何に変換して積を計算するか、よく考えないといけません。2進法のまま計算しても、10進法のまま計算しても、工夫をしないと計算が大変です。
問2は、ベクトルでよく見かける設定です。純粋にベクトルの世界だけで計算していくこともできますが、図形の性質を使うと計算をかなり省略できます。次ページの解説に、図形の性質を使って解く方法を説明しています。
解答編
問題
次の各問に答えよ。
問1 10進法で表された数 $6.75$ を2進法で表せ。また、この数と2進法で表された数 $101.0101$ との積として与えられる数を2進法および4進法で表せ。
解答例
\[ 6.75=2^2+2^1+2^{-1}+2^{-2} \]なので、 $6.75$ を2進法で表すと $110.11_{(2)}$ となる。
また、2進法で表された数 $101.0101$ を10進法で表すと\[ 2^2+2^0+2^{-2}+2^{-4}=5+\frac{5}{16} \]なので、 $6.75$ とこの数との積を10進法で計算すると
\begin{eqnarray}
& &
\left(6+\dfrac{3}{4}\right)\times\left(5+\dfrac{5}{16}\right) \\[5pt]
&=&
30+\frac{15}{8}+\frac{15}{4}+\frac{15}{64} \\[5pt]
&=&
30+\frac{15\cdot(8+16+1)}{64} \\[5pt]
&=&
30+\frac{375}{64} \\[5pt]
&=&
35+\frac{55}{64} \\[5pt]
\end{eqnarray}となる。ここで、\[ 35=2^5+2^1+2^0 \]であり、\[ 55=2^5+2^4+2^2+2^1+2^0 \]で $64=2^6$ なので、この積を2進法で表すと\[ 100011.110111_{(2)} \]となる。
また、\[ 35=2\cdot 4^2+3\cdot 4^0 \]であり、\[ 55=3\cdot 4^2+1\cdot 4^1+3\cdot 4^0 \]で、 $64=4^3$ なので、この積を4進法で表すと\[ 203.313_{(4)} \]となる。
答
$6.75$ を2進法で表したもの: $110.11_{(2)}$
積を2進法で表したもの: $100011.110111_{(2)}$
積を4進法で表したもの: $203.313_{(4)}$
(終)
解説
2進法の小数で表して計算すると、桁が増えて大変です。10進法の小数で表すと、2進法に変換するのが大変です。分数を使うとそこまで複雑にはならないと思います。
解答編 つづき
問2 $\triangle \mathrm{ OAB }$ において $\mathrm{ OA }=3$, $\mathrm{ OB }=2$, $\angle \mathrm{ AOB }=60^{\circ}$ とする。 $\triangle \mathrm{ OAB }$ の垂心を $\mathrm{ H }$ とするとき、 $\overrightarrow{ \mathrm{ OH } }$ を $\overrightarrow{ \mathrm{ OA } }$ と $\overrightarrow{ \mathrm{ OB } }$ を用いて表せ。
解答例
$\mathrm{ AH }$ と $\mathrm{ OB }$ との交点を $\mathrm{ D }$ とし、 $\mathrm{ BH }$ と $\mathrm{ OA }$ との交点を $\mathrm{ E }$ とする。
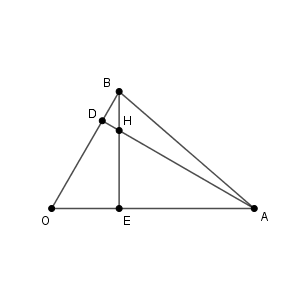
また、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$ 、 $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ とする。
$\angle \mathrm{ AOB }=60^{\circ}$ なので、 $\mathrm{ OD }=3\cos60^{\circ}=\dfrac{3}{2}$ であり、 $\mathrm{ OE }=2\cos60^{\circ}=1$ である。よって、 $\overrightarrow{ \mathrm{ OD } }=\dfrac{3}{4}\vec{b}$ 、 $\overrightarrow{ \mathrm{ OE } }=\dfrac{1}{3}\vec{a}$ とかける。
ここで、 $\mathrm{ AH:HD }=s:(1-s)$ とすると\[ \overrightarrow{ \mathrm{ OH } }=(1-s)\vec{a}+\frac{3s}{4}\vec{b} \]と表すことができる。また、 $\mathrm{ BH:HE }=t:(1-t)$ とすると\[ \overrightarrow{ \mathrm{ OH } }=\frac{t}{3}\vec{a}+(1-t)\vec{b} \]と表すこともできる。ここで、 $\vec{a}, \vec{b}$ は平行ではなく、 $\vec{0}$ でもないので
\begin{eqnarray}
1-s &=& \frac{t}{3} \\[5pt]
\frac{3s}{4} &=& 1-t \\[5pt]
\end{eqnarray}が成り立つ。2つ目の式から $t=1-\dfrac{3s}{4}$ なので、これを1つ目に代入して
\begin{eqnarray}
1-s &=& \frac{1}{3} \left( 1-\dfrac{3}{4}s \right) \\[5pt]
3-3s &=& 1-\dfrac{3}{4}s \\[5pt]
\frac{9}{4}s &=& 2 \\[5pt]
s &=& \frac{8}{9} \\[5pt]
\end{eqnarray}が得られる。これより、\[ \overrightarrow{ \mathrm{ OH } }=\frac{1}{9}\vec{a}+\frac{2}{3}\vec{b} \]となることがわかる。
以上より、 \[ \overrightarrow{ \mathrm{ OH } }=\frac{1}{9}\overrightarrow{ \mathrm{ OA } }+\frac{2}{3}\overrightarrow{ \mathrm{ OB } } \]と表せる。
(終)
解説
ここでは、まじめにベクトルを2種類で表して求めていますが、図形の性質を使えばもっと計算を減らすことができます。

三角形OBE と直線AD に対してメネラウスの定理を使えば
\begin{eqnarray}
\frac{\mathrm{ OA } }{\mathrm{ AE } } \cdot \frac{\mathrm{ EH } }{\mathrm{ HB } } \cdot \frac{\mathrm{ BD } }{\mathrm{ DO } } &=& 1 \\[5pt]
\frac{3}{2} \cdot \frac{\mathrm{ EH } }{\mathrm{ HB } } \cdot \frac{\frac{1}{2} }{\frac{3}{2} } &=& 1 \\[5pt]
\frac{\mathrm{ EH } }{\mathrm{ HB } } &=& 2 \\[5pt]
\end{eqnarray}と求められるので、\[ \overrightarrow{ \mathrm{ OH } }=\frac{\overrightarrow{ \mathrm{ OE } } }{3}+\frac{2}{3}\overrightarrow{ \mathrm{ OB } }=\frac{1}{9}\overrightarrow{ \mathrm{ OA } }+\frac{2}{3}\overrightarrow{ \mathrm{ OB } } \]と求めることもできます。ベクトルの問題で、幾何の性質を使えば簡単に求められる典型です。
また、今の場合は角度が特殊なので、もっと簡単に比を求めることができます。三角形 OBE は正三角形の半分です。 $\mathrm{ BD }=\dfrac{1}{2}$ なので $\mathrm{ BH }=\dfrac{\sqrt{3} }{3}$ であり、 $\mathrm{ BE }=\sqrt{3}$ なので、これからも $\mathrm{ BH:HE }=1:2$ とわかります。





