京都大学 文系 2006年度 第5問 解説
問題編
【問題】
n,kは自然数で$k\leqq n$とする。穴の開いた$2k$個の白玉と$2n-2k$個の黒玉にひもを通して輪を作る。このとき適当な2箇所でひもを切ってn個ずつの2組に分け、どちらの組も白玉k個、黒玉$n-k$個からなるようにできることを示せ。
【考え方】
出ました! よくわからない問題です。問題文にははっきりとは書かれていませんが、白と黒の順番は適当ということでしょう。
まずは、具体的な数を入れて考えてみましょう。$n=3,k=1$としてみます。つまり、玉は全部で6個で、白が2個、黒が4個、ということです。
「黒白黒白黒黒」と並んでいたとしましょう。一番はじめと最後がつながっている、と考えてください。
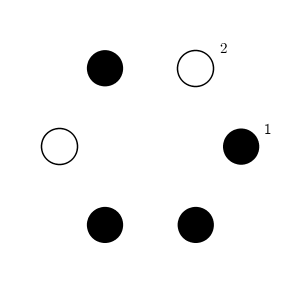
このときは、3個目から5個目までとそれ以外の組に分ければ、「どちらも白1個、黒2個」になります。
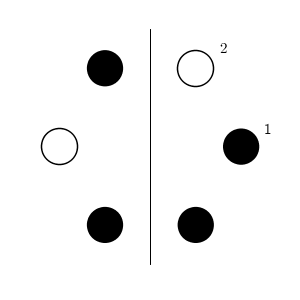
また、「黒白黒黒黒白」と並んでいたら、1個目から3個目までと4個目から6個目までの2組に分ければいいです。
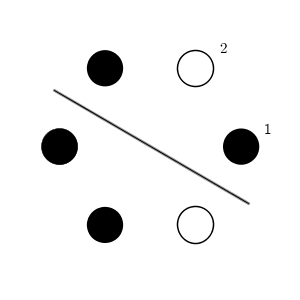
このように、どちらの組も、白玉と黒玉がそれぞれ同じ個数ずつになるように分けることができる、ということですね。もちろん、ひもでつながっているので順番を変えることはできません。
状況は分かったものの、それを説明するのは結構大変です。白と黒の並び方がバラバラなので、組の分け方もいろいろありえます。ここでは、組の分け方を変えると、白と黒の数がどう変わるかに注目して解答していくことにします。
解答編
【問題】
n,kは自然数で$k\leqq n$とする。穴の開いた$2k$個の白玉と$2n-2k$個の黒玉にひもを通して輪を作る。このとき適当な2箇所でひもを切ってn個ずつの2組に分け、どちらの組も白玉k個、黒玉$n-k$個からなるようにできることを示せ。
【解答】
ひもでつながっている順番に、玉に$1$から$2n$まで数字をふる。また、$1\leqq i\leqq n+1$に対し、玉$i$から玉$i+n-1$までの$n$個の玉に含まれている白玉の個数を、$W_i$と書くことにする。
$W_1=a$とする($0\leqq a \leqq 2k$)。このとき、$W_{n+1}=2k-a$である。$0\leqq a \leqq k$のときは$k\leqq 2k-a \leqq 2k$であり、$k\lt a \leqq 2k$のときは$0\leqq 2k-a \lt k$であるので、$k$は常に$a$と$2k-a$の間に含まれる。
$1\leqq i\leqq n$のとき、$W_i$と$W_{i+1}$について考える。この2組は、玉$i$と玉$i+n$以外は同じ玉を対象にしている。よって、$W_i$と$W_{i+1}$の差は、玉$i$と玉$i+n$によって決まる。
この2つの玉が同じ色であれば、$W_i$と$W_{i+1}$は同じ値になり、異なる色であれば、$W_i$と$W_{i+1}$の差は1となる。よって、$W_i$と$W_{i+1}$の差は1以下である。
このことから、$W_1(=a),W_2,\cdots ,W_n,W_{n+1}(=2k-a)$には、$a$から$2k-a$までの整数が少なくとも1回ずつ現れる。$a$と$2k-a$の間には、必ずkが含まれるので、$W_m=k$となる自然数mが存在する($1\leqq m\leqq n+1$)。よって、玉$m$から玉$m+n-1$とそれ以外の組に分けると、どちらの組も「白玉k個、黒玉$n-k$個からなる」ようにできる。
【解答終】
【解説】
$W_i$と$W_{i+1}$について考えるところがわかりにくいかもしれません。
玉$1$から玉$n$までに含まれている白玉と、玉$2$から玉$n+1$までに含まれている白玉の数の差を考えてみましょう。このとき、玉2から玉$n$までは共通です。よって、玉$1$と玉$n+1$の影響しか反映されません。このとき、この2つの玉の色が同じなら白玉の数は不変、違っていたら白玉の差は1となり、どんな組み合わせでも白玉の差は1以下になります。
これは他の組み合わせでも同じです。そのため、$W_i$と$W_{i+1}$の差は1以下となります。$a$と$2k-a$の間を、差が0か1ずつ変化していけば、必ず$k$になるときがあるので、そこで組を分ければいいということですね。
文系だけの問題ですが、理系に出題しても正答率は低かったんじゃないかなぁと思います。説明の難しい問題です。





