センター試験 数学II・数学B 2017年度 第4問 解説
問題編
問題
座標平面上に点 $\mathrm{ A }(2,0)$ をとり、原点 O を中心とする半径が 2 の円周上に点 B, C, D, E, F を、点 A, B, C, D, E, F が順に正六角形の頂点となるようにとる。ただし、 B は第1象限にあるとする。
(1) 点 B の座標は $(\myBox{ア},\sqrt{\myBox{イ}})$ 、点 D の座標は $(-\myBox{ウ},0)$ である。
(2) 線分 BD の中点を M とし、直線 AM と直線 CD の交点を N とする。 $\overrightarrow{ \mathrm{ ON } }$ を求めよう。
$\overrightarrow{ \mathrm{ ON } }$ は実数 r, s を用いて、 $\overrightarrow{ \mathrm{ ON } }=\overrightarrow{ \mathrm{ OA } }+r\overrightarrow{ \mathrm{ AM } }$, $\overrightarrow{ \mathrm{ ON } }=\overrightarrow{ \mathrm{ OD } }+s\overrightarrow{ \mathrm{ DC } }$ と2通りに表すことができる。ここで
\begin{eqnarray} \overrightarrow{ \mathrm{ AM } } &=& \left(-\frac{\myBox{エ}}{\myBox{オ}}, \frac{\sqrt{\myBox{カ}} }{\myBox{キ}}\right) \\[5pt] \overrightarrow{ \mathrm{ DC } } &=& \left(\myBox{ク}, \sqrt{\myBox{ケ}}\right) \\[5pt] \end{eqnarray}であるから\[ r=\frac{\myBox{コ}}{\myBox{サ}}, \ s=\frac{\myBox{シ}}{\myBox{ス}} \]である。よって\[ \overrightarrow{ \mathrm{ ON } } = \left(-\frac{\myBox{セ}}{\myBox{ソ}}, \frac{\myBox{タ}\sqrt{\myBox{チ}} }{\myBox{ツ}}\right) \]である。(3) 線分 BF 上に点 P をとり、その y 座標を a とする。点 P から直線 CE に引いた垂線と、点 C から直線 EP に引いた垂線との交点を H とする。
$\overrightarrow{ \mathrm{ EP } }$ が\[ \overrightarrow{ \mathrm{ EP } } = (\myBox{テ}, \myBox{ト}+\sqrt{\myBox{ナ}}) \]と表せることにより、 H の座標を a を用いて表すと\[ \left(\frac{\myBox{ニ}a^{\myBox{ヌ}}+\myBox{ネ}}{\myBox{ノ}}, \myBox{ハ}\right) \]である。
さらに、 $\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ OH } }$ のなす角を $\theta$ とする。 $\displaystyle \cos\theta = \frac{12}{13}$ のとき、 a の値は\[ a=\pm \frac{\myBox{ヒ}}{\myBox{フヘ}} \]である。
考え方
各点の座標がきれいに求められるので、成分を使ってベクトルを考えていきます。(2)のように、2通りに表してベクトルを求める方法はよく出題されます。
後半は内積を用いた計算です。計算は少し煩雑ですが、最終的には計算しやすい式が出てくるので、根気よく計算しましょう。
解答編
問題
座標平面上に点 $\mathrm{ A }(2,0)$ をとり、原点 O を中心とする半径が 2 の円周上に点 B, C, D, E, F を、点 A, B, C, D, E, F が順に正六角形の頂点となるようにとる。ただし、 B は第1象限にあるとする。
(1) 点 B の座標は $(\myBox{ア},\sqrt{\myBox{イ}})$ 、点 D の座標は $(-\myBox{ウ},0)$ である。
解説
図は次のようになります。
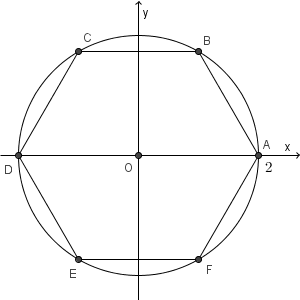
三角形 OAB は正三角形なので、点 B の座標は $(1,\sqrt{3})$ となります。また、点 D の座標は $(-2,0)$ となります。
解答
アイ：13ウ：2
解答編 つづき
問題
(2) 線分 BD の中点を M とし、直線 AM と直線 CD の交点を N とする。 $\overrightarrow{ \mathrm{ ON } }$ を求めよう。
$\overrightarrow{ \mathrm{ ON } }$ は実数 r, s を用いて、 $\overrightarrow{ \mathrm{ ON } }=\overrightarrow{ \mathrm{ OA } }+r\overrightarrow{ \mathrm{ AM } }$, $\overrightarrow{ \mathrm{ ON } }=\overrightarrow{ \mathrm{ OD } }+s\overrightarrow{ \mathrm{ DC } }$ と2通りに表すことができる。ここで
\begin{eqnarray} \overrightarrow{ \mathrm{ AM } } &=& \left(-\frac{\myBox{エ}}{\myBox{オ}}, \frac{\sqrt{\myBox{カ}} }{\myBox{キ}}\right) \\[5pt] \overrightarrow{ \mathrm{ DC } } &=& \left(\myBox{ク}, \sqrt{\myBox{ケ}}\right) \\[5pt] \end{eqnarray}であるから\[ r=\frac{\myBox{コ}}{\myBox{サ}}, \ s=\frac{\myBox{シ}}{\myBox{ス}} \]である。よって\[ \overrightarrow{ \mathrm{ ON } } = \left(-\frac{\myBox{セ}}{\myBox{ソ}}, \frac{\myBox{タ}\sqrt{\myBox{チ}} }{\myBox{ツ}}\right) \]である。
解説
図は次のようになってい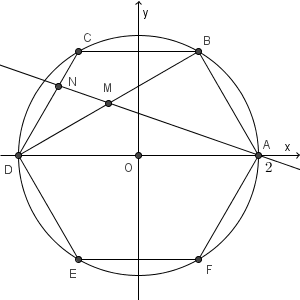ます。
\begin{eqnarray}
\overrightarrow{ \mathrm{ AM } }
&=&
\overrightarrow{ \mathrm{ OM } } -\overrightarrow{ \mathrm{ OA } } \\[5pt]
&=&
\frac{ \overrightarrow{ \mathrm{ OB } }+\overrightarrow{ \mathrm{ OD } } }{2} -\overrightarrow{ \mathrm{ OA } } \\[5pt]
&=&
\left(\frac{1-2}{2}-2, \frac{\sqrt{3}+0}{2}-0\right) \\[5pt]
&=&
\left(-\frac{5}{2}, \frac{\sqrt{3} }{2}\right) \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
\overrightarrow{ \mathrm{ DC } }
&=&
\overrightarrow{ \mathrm{ OC } } -\overrightarrow{ \mathrm{ OD } } \\[5pt]
&=&
\left(-1+2, \sqrt{3}-0\right) \\[5pt]
&=&
\left(1, \sqrt{3}\right) \\[5pt]
\end{eqnarray}となります。
よって、
\begin{eqnarray}
\overrightarrow{ \mathrm{ ON } }
&=&
\overrightarrow{ \mathrm{ OA } }+r\overrightarrow{ \mathrm{ AM } } \\
&=&
\left(2-\frac{5}{2}r, 0+\frac{\sqrt{3} }{2}r\right)
\end{eqnarray}と書け、また、
\begin{eqnarray}
\overrightarrow{ \mathrm{ ON } }
&=&
\overrightarrow{ \mathrm{ OD } }+s\overrightarrow{ \mathrm{ DC } } \\
&=&
\left(-2+s, 0+s\sqrt{3}\right) \\
\end{eqnarray}とも書けることがわかります。どちらで書いても成分は同じなので
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle 2-\frac{5}{2}r = -2+s \\
\displaystyle \frac{\sqrt{3} }{2}r = s\sqrt{3}
\end{array}
\right.
\end{eqnarray}が成り立ちます。2つ目の式から $r=2s$ となるので、これを1つ目の式に入れると
\begin{eqnarray}
2-5s &=& -2+s \\
-6s &=& -4 \\
s&=&\frac{2}{3}
\end{eqnarray}となります。よって、 $\displaystyle r=2s=\frac{4}{3}$ となります。
上で求めた通り、 $\overrightarrow{ \mathrm{ ON } } = \left(-2+s, 0+s\sqrt{3}\right)$ なのでこれに $\displaystyle s=\frac{2}{3}$ を代入して
\begin{eqnarray}
\overrightarrow{ \mathrm{ ON } }
&=&
\left(-2+\frac{2}{3}, \frac{2}{3}\times \sqrt{3}\right) \\[5pt]
&=&
\left(-\frac{4}{3}, \frac{2\sqrt{3} }{3}\right) \\[5pt]
\end{eqnarray}が得られます。
解答
エオカキ：5232クケ：13
コサシス：4323
セソタチツ：43233
解答編 つづき
問題
(3) 線分 BF 上に点 P をとり、その y 座標を a とする。点 P から直線 CE に引いた垂線と、点 C から直線 EP に引いた垂線との交点を H とする。
$\overrightarrow{ \mathrm{ EP } }$ が\[ \overrightarrow{ \mathrm{ EP } } = (\myBox{テ}, \myBox{ト}+\sqrt{\myBox{ナ}}) \]と表せることにより、 H の座標を a を用いて表すと\[ \left(\frac{\myBox{ニ}a^{\myBox{ヌ}}+\myBox{ネ}}{\myBox{ノ}}, \myBox{ハ}\right) \]である。
さらに、 $\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ OH } }$ のなす角を $\theta$ とする。 $\displaystyle \cos\theta = \frac{12}{13}$ のとき、 a の値は\[ a=\pm \frac{\myBox{ヒ}}{\myBox{フヘ}} \]である。
解説
図は次のようになっています。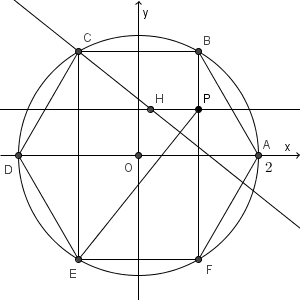
P の x 座標は $1$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ EP } }
&=&
\overrightarrow{ \mathrm{ OP } }-\overrightarrow{ \mathrm{ OE } } \\
&=&
\left(1-(-1),a-(-\sqrt{3})\right)
&=&
\left(2,a+\sqrt{3}\right)
\end{eqnarray}となります。
また、 H の y 座標は a となります。この x 座標を h とすると
\begin{eqnarray}
\overrightarrow{ \mathrm{ CH } }
&=&
\overrightarrow{ \mathrm{ OH } }-\overrightarrow{ \mathrm{ OC } } \\
&=&
\left(h+1,a-\sqrt{3}\right)
\end{eqnarray}となります。 $\overrightarrow{ \mathrm{ EP } }$ と $\overrightarrow{ \mathrm{ CH } }$ は垂直に交わるので、内積は0となることから h は次のように求められます。
\begin{eqnarray}
\overrightarrow{ \mathrm{ EP } } \cdot \overrightarrow{ \mathrm{ CH } } &=& 0 \\
2(h+1)+(a+\sqrt{3})(a-\sqrt{3}) &=& 0 \\
2(h+1) &=& -a^2+3 \\
h &=& \frac{-a^2+3}{2}-1 \\
&=& \frac{-a^2+1}{2} \\
\end{eqnarray}
解答
テトナ：2a3ニヌネノハ：-212a
解答編 つづき
問題
さらに、 $\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ OH } }$ のなす角を $\theta$ とする。 $\displaystyle \cos\theta = \frac{12}{13}$ のとき、 a の値は\[ a=\pm \frac{[ヒ]}{[フヘ]} \]である。
解説
$\overrightarrow{ \mathrm{ OP } }\cdot \overrightarrow{ \mathrm{ OH } } = |\overrightarrow{ \mathrm{ OP } }||\overrightarrow{ \mathrm{ OH } }|\cos\theta$ となることを用いて、 a の値を求めます。
\begin{eqnarray} \mathrm{ OP } &=& \sqrt{1^2+a^2}=\sqrt{a^2+1} \\[5pt] \mathrm{ OH } &=& \sqrt{\left(\frac{-a^2+1}{2}\right)^2+a^2} \\[5pt] &=& \sqrt{\frac{a^4-2a^2+1}{4}+a^2} \\[5pt] &=& \sqrt{\frac{a^4+2a^2+1}{4} } \\[5pt] &=& \frac{a^2+1}{2} \\[5pt] \end{eqnarray}であり、 \begin{eqnarray} \overrightarrow{ \mathrm{ OP } }\cdot \overrightarrow{ \mathrm{ OH } } &=& (1,a)\cdot \left(\frac{-a^2+1}{2}, a\right) \\[5pt] &=& \frac{-a^2+1}{2}+a^2 \\[5pt] &=& \frac{a^2+1}{2} \\[5pt] \end{eqnarray}となるので、上の式に代入すると、次の式が成り立つことがわかります。 \begin{eqnarray} \frac{a^2+1}{2} &=& \sqrt{a^2+1} \cdot \frac{a^2+1}{2} \cdot \frac{12}{13} \\[5pt] 1 &=& \sqrt{a^2+1} \cdot \frac{12}{13} \\[5pt] 12^2 (a^2+1) &=& 13^2 \\[5pt] 144a^2 &=& 25 \\[5pt] a &=& \pm\frac{5}{12} \\[5pt] \end{eqnarray}が得られます。解答
ヒフヘ：512
