センター試験 数学II・数学B 2014年度 第5問 解説
【選択問題】(第3問~第6問から2問選択)
問題編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$次の表は、あるクラスの生徒9人に対して行われた英語と数学のテスト(各20点満点)の得点をまとめたものである。ただし、テストの得点は整数値である。また、表の数値はすべて正確な値であり、四捨五入されていないものとする。
英語 数学 生徒1 9 15 生徒2 20 20 生徒3 18 14 生徒4 18 17 生徒5 $\mathsf{A}$ 8 生徒6 18 $\mathsf{C}$ 生徒7 14 $\mathsf{D}$ 生徒8 15 14 生徒9 18 15 平均値 16.0 15.0 分散 $\mathsf{B}$ 10.00 相関係数 0.500 以下、小数の形で解答する場合、指定された桁数の一つ下の桁を四捨五入し、解答せよ。途中で割り切れた場合、指定された桁まで 0 をマークすること。
(1) 生徒5の英語の得点 $\mathsf{A}$ は $\myBox{アイ}$ 点であり、9人の英語の得点の分散 $\mathsf{B}$ の値は $\myBox{ウエ}.\myBox{オカ}$ である。また、9人の数学の得点の平均値が 15.0 点であることと、英語と数学の得点の相関係数の値が 0.500 であることから、生徒6の数学の得点 $\mathsf{C}$ と生徒7の数学の得点 $\mathsf{D}$ の関係式
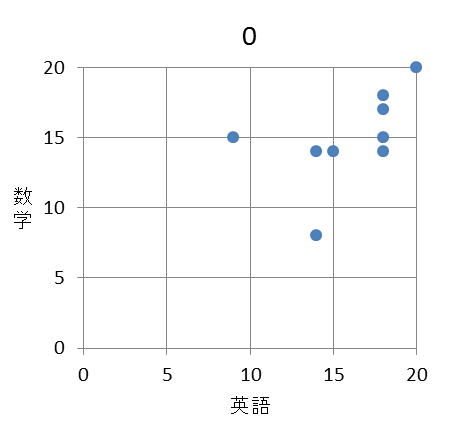
\begin{eqnarray} & & \mathsf{C}+\mathsf{D}=\myBox{キク} \\ & & \mathsf{C}-\mathsf{D}=\myBox{ケ} \end{eqnarray}が得られる。したがって、 $\mathsf{C}$ は $\myBox{コサ}$ 点、$\mathsf{D}$ は $\myBox{シス}$ 点である。(2) 9人の英語と数学の得点の相関図(散布図)として適切なものは $\myBox{セ}$ である。 $\myBox{セ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
(3) 生徒10が転入したので、その生徒に対して同じテストを行った。次の表は、はじめの9人の生徒に生徒10を加えた10人の得点をまとめたものである。ただし、表の数値はすべて正確な値であり、四捨五入されていないものとする。
10人の英語の得点の平均値 $\mathsf{E}$ は $\myBox{ソタ}.\myBox{チ}$ 点であり、生徒10の数学の得点 $\mathsf{F}$ は $\myBox{ツ}$ 点である。
英語 数学 生徒1 9 15 生徒2 20 20 生徒3 18 14 生徒4 18 17 生徒5 $\mathsf{A}$ 8 生徒6 18 $\mathsf{C}$ 生徒7 14 $\mathsf{D}$ 生徒8 15 14 生徒9 18 15 生徒10 6 $\mathsf{F}$ 平均値 $\mathsf{E}$ 14.0 分散 18.00 18.00 相関係数 0.750 (4) 生徒10が転入した後で1人の生徒が転出した。残った9人の生徒について、英語の得点の平均値は10人の平均値と同じ $\mybox{ソタ}.\mybox{チ}$ 点、数学の得点の平均値は10人の平均値と同じ 14.0点であった。転出したのは生徒 $\myBox{テ}$ である。また、英語について、10人の得点の分散の値を v, 残った9人の得点の分散の値を $v'$ とすると\[ \frac{v'}{v} = \myBox{ト} \]が成り立つ。さらに、10人についての英語と数学の得点の相関係数の値を r, 残った9人についての英語と数学の得点の相関係数の値を $r'$ とすると\[ \frac{r'}{r} = \myBox{ナ} \]が成り立つ。 $\myBox{ト}$, $\myBox{ナ}$ に当てはまるものを、次の 0 ~ 5 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $-1$, 1: $1$, 2: $\dfrac{9}{10}$, 3: $\left(-\dfrac{9}{10}\right)^2$, 4: $\dfrac{10}{9}$, 5: $\left(\dfrac{10}{9}\right)^2$
考え方
(1)で細かな計算をさせられます。定義通りに計算するだけですが、ここを間違うと後に響いてくるので、計算の見直しをよくしましょう。
(2)は(1)が正しく計算できないとできません。消去法で求めましょう。
(3)は(1)が正しく出せなくても出すことはできます。和を計算しなくても、9人の平均値から9人の和を求めることができます。無駄な計算はしないようにしましょう。
(4)は、平均・分散・相関係数の求め方をよく理解しておかないと、解くことは難しいです。値が抜けることで、計算式のどの部分が変化するのかよく考えて解くようにしましょう。
【選択問題】(第3問~第6問から2問選択)
解答編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$次の表は、あるクラスの生徒9人に対して行われた英語と数学のテスト(各20点満点)の得点をまとめたものである。ただし、テストの得点は整数値である。また、表の数値はすべて正確な値であり、四捨五入されていないものとする。
英語 数学 生徒1 9 15 生徒2 20 20 生徒3 18 14 生徒4 18 17 生徒5 $\mathsf{A}$ 8 生徒6 18 $\mathsf{C}$ 生徒7 14 $\mathsf{D}$ 生徒8 15 14 生徒9 18 15 平均値 16.0 15.0 分散 $\mathsf{B}$ 10.00 相関係数 0.500 以下、小数の形で解答する場合、指定された桁数の一つ下の桁を四捨五入し、解答せよ。途中で割り切れた場合、指定された桁まで 0 をマークすること。
(1) 生徒5の英語の得点 $\mathsf{A}$ は $\myBox{アイ}$ 点であり、9人の英語の得点の分散 $\mathsf{B}$ の値は $\myBox{ウエ}.\myBox{オカ}$ である。
解説
「全員の英語の点数を足して9で割ったものが平均値16.0になる」という条件式から生徒5の英語の点数を求めることができます。が、ここでは、各生徒の英語の点数から16点引いたものを考えましょう。このとき、平均は0になり、和も0になります。
16点を引いたとき、生徒1から生徒4までの和は\[ -7+4+2+2=1 \]となり、生徒6から生徒9までの和は\[ 2-2-1+2=1 \]となります。全員を足すと0になるので
\begin{eqnarray}
1+(\mathsf{A}-16)+1 &=& 0 \\
\mathsf{A} &=& 14 \\
\end{eqnarray}と求められます。
英語の分散は、それぞれの「平均との差の2乗」を計算し、その和を個数9で割って求めることができます。よって
\begin{eqnarray}
& &
\frac{1}{9}\{ (-7)^2+4^2+2^2+2^2+(-2)^2+2^2+(-2)^2+(-1)^2+2^2 \} \\[5pt]
&=&
\frac{1}{9}\{ 49+16+4+4+4+4+4+1+4 \} \\[5pt]
&=&
10
\end{eqnarray}と求められます。
解答
アイ:14
ウエオカ:1000
参考
解答編 つづき
問題
また、9人の数学の得点の平均値が 15.0 点であることと、英語と数学の得点の相関係数の値が 0.500 であることから、生徒6の数学の得点 $\mathsf{C}$ と生徒7の数学の得点 $\mathsf{D}$ の関係式
\begin{eqnarray} & & \mathsf{C}+\mathsf{D}=\myBox{キク} \\ & & \mathsf{C}-\mathsf{D}=\myBox{ケ} \end{eqnarray}が得られる。したがって、 $\mathsf{C}$ は $\myBox{コサ}$ 点、$\mathsf{D}$ は $\myBox{シス}$ 点である。
解説
先ほどと同様に、平均値15.0を引いたものの和が0になることを使いましょう。生徒1から生徒9までの和を考えると\[ 0+5-1+2-7+(\mathsf{C}-15)+(\mathsf{D}-15)-1+0 = 0 \]が成り立つので、\[ \mathsf{C}+\mathsf{D} = 32 \]が得られます。
相関係数は、共分散をそれぞれの標準偏差で割ったものです。どちらも分散は 10.00 なので、共分散を 10 で割れば、相関係数が出てきます。
共分散は、それぞれの「平均との差同士を掛け合わせたもの」を計算し、その和を個数9で割ったものです。平均との差同士を掛け合わせたものは、次のようになります。
生徒1: $-7 \times 0 = 0$
生徒2: $ 4 \times 5 = 20$
生徒3: $ 2 \times -1 = -2$
生徒4: $ 2 \times 2 = 4$
生徒5: $-2 \times -7 = 14$
生徒6: $ 2 \times (\mathsf{C}-15)$
生徒7: $-2 \times (\mathsf{D}-15)$
生徒8: $-1 \times -1 = 1$
生徒9: $ 2 \times 0 = 0$
この和を9で割ったものが共分散なので、共分散は次のようになります。
\begin{eqnarray}
& &
\frac{1}{9}(20-2+4+14+2\mathsf{C}-30-2\mathsf{D}+30+1) \\[5pt]
&=&
\frac{1}{9}(2\mathsf{C}-2\mathsf{D}+37) \\[5pt]
\end{eqnarray}
これを10で割ったものが相関係数になるので、
\begin{eqnarray}
\frac{1}{9}(2\mathsf{C}-2\mathsf{D}+37) \div 10 &=& 0.5 \\[5pt]
2\mathsf{C}-2\mathsf{D}+37 &=& 45 \\[5pt]
\mathsf{C}-\mathsf{D} &=& 4 \\[5pt]
\end{eqnarray}が得られます。
2つの式を辺々足すと $2\mathsf{C} = 36$ から $\mathsf{C}=18$ とわかり、 $\mathsf{D}=14$ もわかります。
解答
キクケ:324コサシス:1814
参考
解答編 つづき
問題
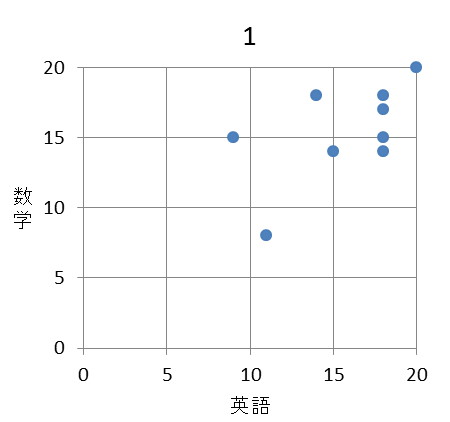
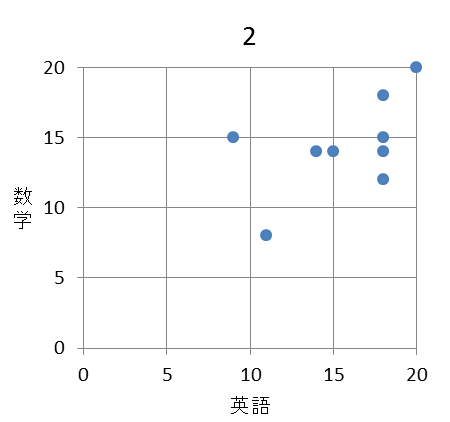
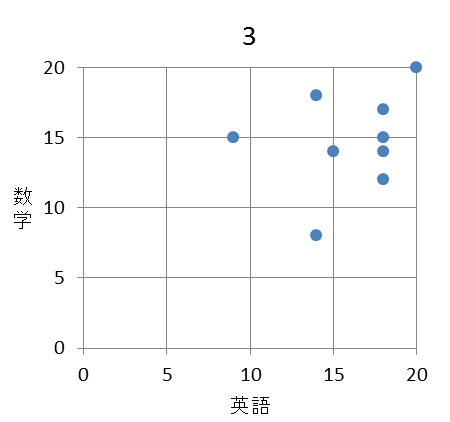
(2) 9人の英語と数学の得点の相関図(散布図)として適切なものは $\myBox{セ}$ である。 $\myBox{セ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
解説
各グラフの違いを見つけて、消去法で考えていきます。
まず、数学が8点の部分に注目すると、英語が11点と14点のものがあります。数学が8点なのは生徒5であり、英語の点数は $\mathsf{A}=14$ なので、選択肢の1と2が消えます。
選択肢の0と3を見比べると、英語が14点の部分で違いがあります。片方は14点、もう片方は18点です。英語が14点の生徒のうち数学が8点でない生徒を表から探すと、生徒7であることがわかります。 $\mathsf{D}=14$ なので、選択肢3が消え、選択肢0が正解であることがわかります。
今までの計算が合っていないと、ここも自動的に間違いを選ぶことになってしまいます。
解答
セ:0解答編 つづき
問題
(3) 生徒10が転入したので、その生徒に対して同じテストを行った。次の表は、はじめの9人の生徒に生徒10を加えた10人の得点をまとめたものである。ただし、表の数値はすべて正確な値であり、四捨五入されていないものとする。
10人の英語の得点の平均値 $\mathsf{E}$ は $\myBox{ソタ}.\myBox{チ}$ 点であり、生徒10の数学の得点 $\mathsf{F}$ は $\myBox{ツ}$ 点である。
英語 数学 生徒1 9 15 生徒2 20 20 生徒3 18 14 生徒4 18 17 生徒5 $\mathsf{A}$ 8 生徒6 18 $\mathsf{C}$ 生徒7 14 $\mathsf{D}$ 生徒8 15 14 生徒9 18 15 生徒10 6 $\mathsf{F}$ 平均値 $\mathsf{E}$ 14.0 分散 18.00 18.00 相関係数 0.750
解説
生徒1から生徒9までの英語の平均点は16点だったので、9人の英語の点数の和は $16\times 9=144$ 点となります。よって、10人の平均値は\[ (144+6)\div10=15 \]点となることがわかります。
9人の数学の平均点は15点だったので、10人の平均点が14.0点ということから次の式が成り立ちます。
\begin{eqnarray}
(15\times 9+\mathsf{F})\div 10 &=& 14 \\
135+\mathsf{F} &=& 140 \\
\mathsf{F}&=&5
\end{eqnarray}よって、生徒10の数学の点数は5点だとわかります。
解答
ソタチ:150
ツ:5
参考
解答編 つづき
問題
(4) 生徒10が転入した後で1人の生徒が転出した。残った9人の生徒について、英語の得点の平均値は10人の平均値と同じ $\mybox{ソタ}.\mybox{チ}$ 点、数学の得点の平均値は10人の平均値と同じ 14.0点であった。転出したのは生徒 $\myBox{テ}$ である。
解説
「値を取り除いても平均値が変化しない」ということは、その値と平均値が等しいということです。もし取り除いた値が平均値より低ければ、取り除いた後は平均値が改善しますし、高ければ平均値は悪化してしまいます。このことは、テストの平均点を考えれば、理解しやすいと思います。
平均値が変わらなかったことから、英語の点数は平均値と同じ15点、数学の点数も平均値と同じ14点であることがわかるので、抜けた生徒は生徒8であることがわかります。
解答
テ:8
解答編 つづき
問題
また、英語について、10人の得点の分散の値を v, 残った9人の得点の分散の値を $v'$ とすると\[ \frac{v'}{v} = \myBox{ト} \]が成り立つ。さらに、10人についての英語と数学の得点の相関係数の値を r, 残った9人についての英語と数学の得点の相関係数の値を $r'$ とすると\[ \frac{r'}{r} = \myBox{ナ} \]が成り立つ。 $\myBox{ト}$, $\myBox{ナ}$ に当てはまるものを、次の 0 ~ 5 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: $-1$, 1: $1$, 2: $\dfrac{9}{10}$, 3: $\left(-\dfrac{9}{10}\right)^2$, 4: $\dfrac{10}{9}$, 5: $\left(\dfrac{10}{9}\right)^2$
解説
分散は、それぞれの「平均との差の2乗」を計算し、その和を個数で割って求めます。転出した生徒の点数は平均と等しいことから、「平均との差の2乗」の和は変化しません。よって、変わるのは割る数だけです。
「平均との差の2乗」の和を S とすると、10人の得点の分散 v は $\displaystyle v=\frac{S}{10}$ となり、9人の得点の分散 $v'$ は $\displaystyle v' = \frac{S}{9}$ となります。よって
\begin{eqnarray}
\frac{v'}{v} = \frac{S}{9} \div \frac{S}{10} = \frac{10}{9}
\end{eqnarray}となります。
相関係数は、共分散をそれぞれの標準偏差で割ったものです。上と同様に考えれば、どちらの場合も、9人のときの分散は10人のときの分散の $\displaystyle \frac{10}{9}$ 倍になります。
共分散は、それぞれの「平均との差同士を掛け合わせたもの」を計算し、その和を個数で割ったものです。転出した生徒の点数は平均と等しかったので、「平均との差同士を掛け合わせたもの」の和も変化しません。よって、割る数だけが変わります。こちらも、先ほどと同じように考えると、9人のときの共分散が10人のときの共分散の $\displaystyle \frac{10}{9}$ 倍になることがわかります。
割る数も割られる数も $\displaystyle \frac{10}{9}$ 倍になるので、相関係数自体は変化しません。
なお、イメージでいうと、「分散」とは「平均からの散らばり」を表す指標です。そのため、「平均と同じ値」がなくなれば、散らばり度合いは高まってしまいます。なので、この問題では9人になったほうが散らばりは大きくなるはずで、トに入る数字は1より大きい数字であると考えることができます。
また、相関係数とは、平均を基準に考えたときに、「片方が増えたらもう片方も増える」という傾向を表すものです。「平均と同じ値」があってもなくても、この傾向は変化しないので、ナに入る数字は1だと考えることもできます。
イメージではなく、数式で考えるとはじめに書いた考え方になります。