東京大学 理系 2017年度 第1問 解説
問題編
問題
実数 a, b に対して\[ f(\theta)=\cos 3\theta +a\cos 2\theta +b\cos\theta \]とし、 $0\lt\theta \lt \pi$ で定義された関数\[ g(\theta)=\frac{f(\theta)-f(0)}{\cos\theta-1} \]を考える。
(1) $f(\theta)$ と $g(\theta)$ を $x=\cos\theta$ の整式で表せ。
(2) $g(\theta)$ が $0\lt \theta \lt\pi$ の範囲で最小値 $0$ をとるための a, b についての条件を求めよ。また、条件を満たす点 $(a,b)$ が描く図形を座標平面上に図示せよ。
考え方
(1)は、三倍角、倍角の公式を使って、 $\cos\theta$ だけの式に変形します。 $g(\theta)$ は、 $\theta=0$ のとき、つまり、 $x=1$ のときに、分母も分子も0になるので、分子は分母で割り切れることに注意します。
(2)は、軸に文字が入った場合の、二次関数の最小値を考える問題です。軸の位置に分けて場合分けをします。区間の両端が区間に含まれていないことに注意しましょう。
解答編
問題
実数 a, b に対して\[ f(\theta)=\cos 3\theta +a\cos 2\theta +b\cos\theta \]とし、 $0\lt\theta \lt \pi$ で定義された関数\[ g(\theta)=\frac{f(\theta)-f(0)}{\cos\theta-1} \]を考える。
(1) $f(\theta)$ と $g(\theta)$ を $x=\cos\theta$ の整式で表せ。
(2) $g(\theta)$ が $0\lt \theta \lt\pi$ の範囲で最小値 $0$ をとるための a, b についての条件を求めよ。また、条件を満たす点 $(a,b)$ が描く図形を座標平面上に図示せよ。
解答
(1)
\begin{eqnarray}
f(\theta)
&=&
\cos 3\theta +a\cos 2\theta +b\cos\theta \\
&=&
(4\cos^3 \theta-3\cos\theta) +a(2\cos^2\theta-1) +b\cos\theta \\
&=&
4\cos^3 \theta +2a\cos^2\theta+(b-3)\cos\theta -a
\end{eqnarray}なので、 $x=\cos\theta$ とすると $f(\theta)$ は\[ 4x^3+2ax^2+(b-3)x-a \]と表すことができる。
また\[ f(0)=1+a+b \]なので $g(\theta)$ は
\begin{eqnarray}
& &
\frac{4x^3+2ax^2+(b-3)x-a -(1+a+b)}{x-1} \\[5pt]
&=&
\frac{4x^3+2ax^2+(b-3)x-2a-b-1}{x-1} \\[5pt]
&=&
4x^2 +(2a+4)x +2a+b+1
\end{eqnarray}と表すことができる。
(2)
$h(x)=4x^2 +(2a+4)x +2a+b+1$ とおく。 $0\lt\theta\lt\pi$ のとき、 $-1\lt x\lt 1$ なので、この範囲を x が動くときに $h(x)$ の最小値が $0$ となるための条件を求めればよい。
この放物線の軸は $x=-\dfrac{a+2}{4}$ であるから、 $-\dfrac{a+2}{4} \leqq -1$ のときは $y=h(x)$ は単調増加となり、 $-1\lt x\lt 1$ の範囲で最小値をとらない。また、 $-\dfrac{a+2}{4} \geqq 1$ のときは $y=h(x)$ は単調減少となり、 $-1\lt x\lt 1$ の範囲で最小値をとらない。
よって、以下では $-1 \lt -\dfrac{a+2}{4} \lt 1$ とする。これを解くと
\begin{eqnarray}
& & -1 \lt -\dfrac{a+2}{4} \lt 1 \\[5pt]
& & -4 \lt -a-2 \lt 4 \\[5pt]
& & -2 \lt -a \lt 6 \\[5pt]
& & -6 \lt a \lt 2 \\[5pt]
\end{eqnarray}となるので、この範囲で考える。
このとき、 $y=h(x)$ は頂点で最小値をとるので、最小値が $0$ となるのは
\begin{eqnarray}
-\frac{a^2}{4}+a+b &=& 0 \\[5pt]
b &=& \frac{1}{4}a^2-a \\[5pt]
&=& \frac{1}{4}(a-2)^2-1 \\[5pt]
\end{eqnarray}となるときであり、この条件を満たすとき、 $y=h(x)$ は $x=-\dfrac{a+2}{4}$ のときに最小値 $0$ をとる。
よって、求める条件は「 $-6 \lt a \lt 2$ かつ $b= \dfrac{1}{4}a^2-a$ 」であり、これを満たす点 $(a,b)$ の描く図形は次の実線部分(両端の点は含まない)となる。
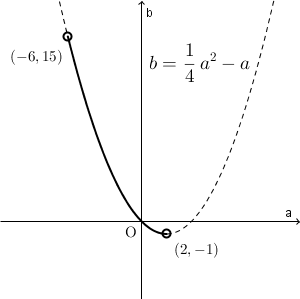
(終)
解説
(1)は、三倍角、倍角の公式を使って、 $\cos\theta$ だけの式にします。 $g(\theta)$ の分子は $x=1$ としたときに0となることから、分母で割り切れることに注意しましょう。
(2)は、軸に文字が含まれているときの二次関数の最小値の問題です。最小値をとる場所が軸の位置によって異なるので、場合を分けて考えます。軸が区間内にない場合、単調増加や単調減少となり、区間の両端が区間に含まれていないことから最小値をとることはありません。
このことから、軸が区間内にある場合だけを考えればよく、頂点の y 座標が0になる条件を考えて解くことができます。





