東京大学 理系 2015年度 第1問 解説
問題編
問題
正の実数 a に対して、座標平面上で次の放物線を考える。
\[
C:y=ax^2+\frac{1-4a^2}{4a}
\]
a が正の実数全体を動くとき、 C の通過する領域を図示せよ。
考え方
この問題は、2通りの解き方が考えられます。1つは、まずxを固定し、aを動かした時のyがとりうる範囲を求め、次にxも動かす、というやり方。もう1つは、元の式をaに関する式として考え、正の実数解をもつようなxとyを求める、というやり方です。
前者は思いつきやすい一方、少しだけ計算が必要になります。後者の解き方はちょっと数学的なセンスが必要な解法ですが、計算はずいぶん楽になります。それぞれ見ていきましょう。
解答編
問題
正の実数 a に対して、座標平面上で次の放物線を考える。
\[
C:y=ax^2+\frac{1-4a^2}{4a}
\]
a が正の実数全体を動くとき、 C の通過する領域を図示せよ。
解答
$x=k$ のとき、y の取りうる値を求める。
このとき、
\begin{eqnarray}
y
&=& ak^2+\frac{1-4a^2}{4a} \\
&=& (k^2-1)a+\frac{1}{4a}
\end{eqnarray}とかける。この式の右辺を $f(a)$ とおき、 $a\gt 0$ の範囲でとりうる値を求める。
ここで、
\begin{eqnarray}
f'(a)
&=& k^2-1 -\frac{1}{4a^2}
\end{eqnarray}なので、 $f'(a)=0$ となる $a \gt 0$ が存在するのは、 $k^2-1 \gt 0$ のときで、そのときの a の値は、 $\displaystyle \frac{1} {2\sqrt{k^2-1} }$ となる。
(1) $k^2 \lt 1$ のとき
$f'(a)$ は常に負であるから、 $f(a)$ は単調減少。また、 $\displaystyle \lim_{a \to +0}f(a)=\infty$ 、 $\displaystyle \lim_{a \to \infty}f(a)=-\infty$ なので、 $f(a)$ はすべての実数値をとりうる。
(2) $k^2 = 1$ のとき
$\displaystyle f(a) = \frac{1}{4a}$ なので、 $a\gt 0$ のとき、 $f(a)$ はすべての正の実数値をとりうる。
(3) $k^2 \gt 1$ のとき
$\displaystyle \lim_{x \to +0}f(a)=\infty$ 、 $\displaystyle \lim_{x \to \infty}f(a)=\infty$ である。また、
\begin{eqnarray}
f\left(\frac{1}{2\sqrt{k^2-1} } \right)
&=& \frac{k^2-1}{2\sqrt{k^2-1} } + \frac{2\sqrt{k^2-1} }{4} \\ \\
&=& \sqrt{k^2-1}
\end{eqnarray}なので、増減表は次のようになる。
\begin{array}{c|ccccc}
a & 0 & \cdots & \frac{1}{2\sqrt{k^2-1} } & \cdots & \infty \\
\hline
f'(a) & & - & 0 & + & \\
\hline
f(a) & \infty & \searrow & \sqrt{k^2-1} & \nearrow & \infty
\end{array}
よって、 $f(a) \geqq \sqrt{k^2-1}$ であり、 $f(a)$ はこの範囲の値をすべてとりうる。
(1)(2)(3)より、求める領域は次のようになる。
$-1 \lt x \lt 1$ のときは、$y$ はすべての実数値
$x=\pm 1$ のときは、$y \gt 0$
$x\lt -1, x \gt 1$ のときは、 $y\geqq \sqrt{x^2-1}$
これを図示すると、次の通りとなる。ただし、境界線は、$y = \sqrt{x^2-1}$ の $y \gt 0$ の部分のみ含む。
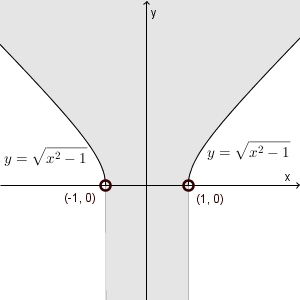
(解答終)
解説
解答の途中で、「$f(a) \geqq \sqrt{k^2-1}$ であり、 $f(a)$ はこの範囲の値をすべてとりうる」と書いていますが、ここを「$f(a) \geqq \sqrt{k^2-1}$ である」と書くのはよくありません。
例えば、このとき「$f(a) \gt 0$ である」も正しい文ですが、 $f(a)$ が $0$と$\sqrt{k^2-1}$ の間の値をとることはありません。 $f(a)$ について求めたいのは、 $f(a)$ が満たす不等式ではなく、 $f(a)$ がとりうる値の範囲なので、「 $f(a)$ はこの範囲の値をすべてとりうる」ということを書かないと求められている答えにはなりません。
解答の流れから伝わるかもしれませんが、丁寧に書いておいて損はないと思います。
続いて、a に関する式として考えるパターンで解いてみます。
別解編
問題
正の実数 a に対して、座標平面上で次の放物線を考える。
\[
C:y=ax^2+\frac{1-4a^2}{4a}
\]
a が正の実数全体を動くとき、 C の通過する領域を図示せよ。
別解
C の式は、次のように変形できる。
\begin{eqnarray}
4ay = 4 a^2 x^2+1-4a^2 \\
(4x^2-4)a^2 -4ya +1 = 0
\end{eqnarray}この式の左辺を $g(a)$ とおく。
(1) $x^2=1$ のとき
このとき、 $g(a)=-4ya+1$ である。よって、 $g(a)=0$ となるとき、 $a=\frac{1}{4y}$ となる。だから、$g(a)=0$ が正の解をもつことと、 $y \gt 0$ であることは同値である。
(2) $x^2 \lt 1$ のとき
$g(a)$ は上に凸であり、 $g(0) = 1 \gt 0$ なので、 $g(a)=0$ は必ず正の解をもつ。よって、このとき $y$ は任意である。
(3) $x^2 \gt 1$ のとき
$g(a)$ は下に凸であり、 $g(0) = 1 \gt 0$ である。よって、「 $g(a)=0$ が正の解をもつこと」は、「 $g(a)=0$ が実数解を持ち、軸が $a=0$ より右にあること」と同値である。
ここで、 $g(a)=0$ が実数解をもつことは
\begin{eqnarray}
(-4y)^2 - 4 (4x^2-4) \geqq 0 \\
y^2 - x^2 + 1 \geqq 0 \\
\end{eqnarray}と同値である。
また、軸は、 $\displaystyle a=\frac{2y}{4x^2-4}$ である。 $x^2 \gt 1$ だから $4x^2-4 \gt 0$ なので、この軸が $a = 0$ より右にあることは、 $y \gt 0$ と同値である。
あわせると、$x$ と $y$ の条件は、 $y \geqq \sqrt{x^2 - 1}$ と書ける( $y \gt 0$ と $x^2 \gt 1$ に注意)。
以上より、(1)(2)(3)から、求める領域は次のようになる。
$-1 \lt x \lt 1$ のときは、$y$ はすべての実数値
$x=1, -1$ のときは、$y \gt 0$
$x\lt -1, x \gt 1$ のときは、$y\geqq \sqrt{x^2-1}$
これを図示すると、次の通りとなる。ただし、境界線は、 $y = \sqrt{x^2-1}$ の $y \gt 0$ の部分のみ含む。

(別解終)
解説
$g(a)$ とおいた式は、 $4x^2-4$ が0なら $a$ の1次式、正なら2次式(グラフは下に凸)、負なら2次式(グラフは上に凸)というように、 $4x^2-4$ の値によって関数の状況が異なってきます。ですので、この値に基づいて場合分けをする必要があります。





