【標準】ベクトルの成分と分解

🕒 2017/08/21 🔄 2024/07/06

ここでは、ベクトルの成分を使って、ベクトルを分解する方法を見ていきます。

📘 目次

ベクトルの分解の復習

【基本】ベクトルの分解で見たように、ベクトルの分解とは、あるベクトルを平行ではない2つのベクトルで表現することです。

もう少し具体的に書きましょう。2つの平行ではないベクトル $\vec{a}$, $\vec{b}$ を使って、 $\vec{p}$ に対して\[ \vec{p}=s\vec{a}+t\vec{b} \]と書くことが、ベクトルの分解です。上のリンク先で見たように、どんなベクトルでもこのように分解でき、しかも、この分解の仕方は1通り（つまり、 s, t の組合せは1組）になります。

以下では、ベクトルの成分を使って、ベクトルの分解を行ってみましょう。

ベクトルの成分とベクトルの分解

例題

$\vec{a}=(1,1)$, $\vec{b}=(1,-1)$, $\vec{p}=(3,-1)$ とする。このとき、\[ \vec{p}=s\vec{a}+t\vec{b} \]を満たす s, t を求めなさい。

図をかくと、次のようになります。わかりやすいように、原点を基準としています。

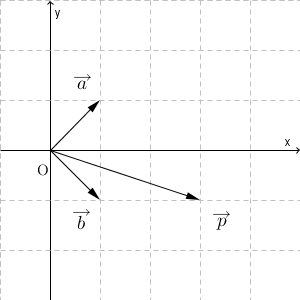
成分を使わずに考えるならば、次のように図の上で分解することになります。

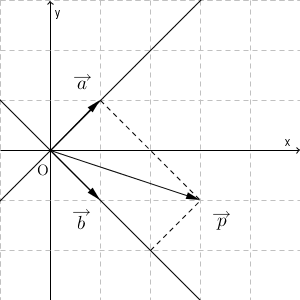
これはきれいに分解できますが、いつもこううまくいくとは限りません。いつもきれいな数字になるとは限りませんからね。ルートなどが出てくると、図で求めるのは難しくなります。

しかし、成分で考えれば、以下のように計算で求めることができます。

$\vec{a}$, $\vec{b}$ は平行ではないので、どんなベクトルでも、 $s\vec{a}+t\vec{b}$ の形に分解できるのでしたね。なので、 $\vec{p}=(3,-1)$ も分解できます。これを成分で書いてみると、次のようになります。
\begin{eqnarray} (3,-1) &=& s(1,1)+t(1,-1) \\[5pt] &=& (s+t,s-t) \\[5pt] \end{eqnarray}ベクトルが等しいことと成分が等しいことが同値であることを暗に使っています（参考：【基本】ベクトルの成分）。

この成分の比較から、2つの式が得られます。\[ s+t=3,\ s-t=-1 \]2つの式を辺々足せば、 $s=1$ が得られます。これを1つ目の式に代入して、 $t=2$ が得られます。よって答えは、\[ (s,t)=(1,2) \]となります。

実際、\[ \vec{p}=\vec{a}+2\vec{b} \]と書けることは、上の図とあっていますね。

この例題では、 $\vec{p}=(3,-1)$ というベクトルを分解しましたが、他のベクトルでも $\vec{a}$, $\vec{b}$ を使って分解できます。そのため、 $\vec{a}$, $\vec{b}$ は新しい軸のように扱えます。今まで使っていた座標では、縦と横にしか分解できませんでしたが、これからは好きな2方向を基準として分解できるんですね。これにより、問題が解きやすくなるケースが増えます。先に進んでいくと実感できるでしょう。

また、上の例題を解いていく中で、連立方程式が出てきましたね。2つの成分を比較するところです。この連立方程式が解けるためには、基準となる2つのベクトル（上の例題では $\vec{a}$, $\vec{b}$ ）が平行でないことが必要です。また、もちろん、 $\vec{0}$ であってもいけません。これらの条件は、地味ですが重要です。特に、文字で考えている場合は、これらの条件を満たしていない状況をスルーしやすいので注意が必要です。