【標準】三角比の二次関数

🕒 2016/10/06 🔄 2023/05/01

ここでは、三角比を含んだ二次関数の最大・最小を考えます。三角比の相互関係の中に2乗を含むものがあったので、二次関数と組み合わせた問題が出題されることもよくあります。範囲に注意して考えていきましょう。

📘 目次

例題

$0^{\circ}\leqq \theta \leqq 180^{\circ}$ のとき、関数 $y=\sin^2\theta+\cos\theta$ の最大値・最小値を求めなさい。また、その値をとるときの $\theta$ も求めなさい。

まずは、三角比の相互関係を使って $\cos$ だけの式にします。その後は、二次関数の最大・最小を求める問題として解きます。
\begin{eqnarray} y &=& \sin^2\theta+\cos\theta \\ &=& (1-\cos^2\theta)+\cos\theta \\ &=& -\cos^2\theta+\cos\theta+1 \\ \end{eqnarray}ここで、$\cos\theta=t$ とすると、 $y=-t^2+t+1$ となるので、これの最大・最小を考えればいいんですね。ただし、範囲に注意しないといけません。 $0^{\circ}\leqq \theta \leqq 180^{\circ}$ なので、 $-1\leqq t\leqq 1$ です。この範囲で、最大・最小を考えます。二次関数の最大・最小があやしい人は、【基本】二次関数の最大・最小（定義域に制限あり）を見てみましょう。 \begin{eqnarray} y &=& -t^2+t+1 \\ &=& -(t^2-t)+1 \\ &=& -\left(t-\frac{1}{2}\right)^2+\frac{1}{4}+1 \\[5pt] &=& -\left(t-\frac{1}{2}\right)^2+\frac{5}{4} \\[5pt] \end{eqnarray}となります。よって、このときのグラフは、次のようになります。

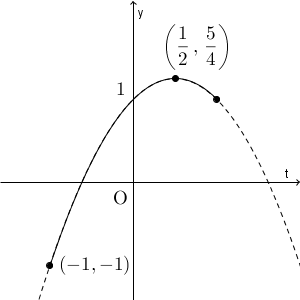
このグラフから、最大値は $\displaystyle \frac{5}{4}$ で、そのとき $\displaystyle t=\frac{1}{2}$ となります。 $\displaystyle \cos\theta=\frac{1}{2}$ ということなので、 $\theta=60^{\circ}$ のとき、ということがわかります。

一方、最小値は $-1$ で、 $t=-1$ のとき、つまり、 $\theta=180^{\circ}$ のとき、となります。