【標準】三角比を含んだ不等式

🕒 2016/10/04 🔄 2023/05/01

前に三角比を含んだ方程式を取り上げました（参考：【基本】三角方程式）。方程式もあるんだから、やはり不等式もあるんですね。ここでは、三角比を含んだ不等式を見ていきます。

なお、「三角不等式」というと、数学の世界では別のことを指す場合があるので、ここでは「三角比を含んだ不等式」と呼んでいます。

📘 目次

sinを含んだ不等式

例題1

$0^{\circ}\leqq\theta\leqq180^{\circ}$ のとき、次を満たす $\theta$ の範囲を求めなさい。
\[ \sin\theta \geqq \frac{1}{\sqrt{2} } \]

方程式のときと同じように単位円を考えて解きます。 $\sin$ は y 座標に対応していましたね（参考：【基本】よく出る0度から180度までの三角比の値）。y 座標が $\displaystyle \frac{1}{\sqrt{2} }$ 以上の部分は、図の赤い部分に対応します。

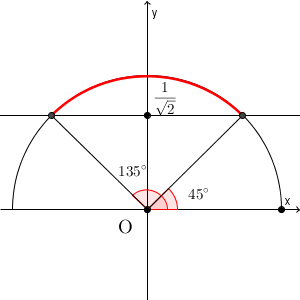
$\displaystyle \sin\theta = \frac{1}{\sqrt{2} }$ を満たす $\theta$ は、 $45^{\circ},135^{\circ}$ であり、この間の部分が条件を満たすので、\[ 45^{\circ}\leqq \theta \leqq 135^{\circ} \]が解となります。

cosを含んだ不等式

例題2

$0^{\circ}\leqq\theta\leqq180^{\circ}$ のとき、次を満たす $\theta$ の範囲を求めなさい。
\[ \cos\theta \lt \frac{1}{2} \]

これも単位円を考えて解きます。 $\cos$ は x 座標に対応していました。x 座標が $\displaystyle \frac{1}{2}$ より小さい部分は、図の赤い部分に対応します。

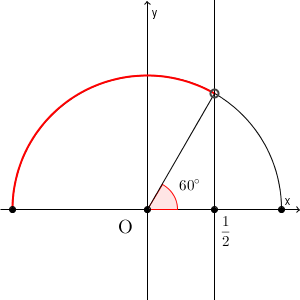
$\displaystyle \cos\theta = \frac{1}{2}$ を満たす $\theta$ は、 $60^{\circ}$ です。これより大きい角度が条件を満たすので、\[ 60^{\circ} \lt \theta \leqq 180^{\circ} \]が解となります。範囲の片方にはイコールがなく、片方にはイコールが入っている点に注意しましょう。

tanを含んだ不等式

例題3

$0^{\circ}\leqq\theta\leqq180^{\circ}$ のとき、次を満たす $\theta$ の範囲を求めなさい。
\[ \tan\theta \leqq 1 \]

最後は $\tan$ です。 $\tan$ は傾きに対応していました。これは、 $x=1$ のときの y 座標でもあるので、直線 $x=1$ で考えると、次の青い部分が対象となります。

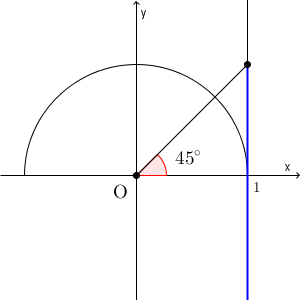
これが単位円周上の点とどう対応するかは、下の図を見てイメージしましょう。傾きが1以下となる部分は、次の図の赤い部分であることが分かります。

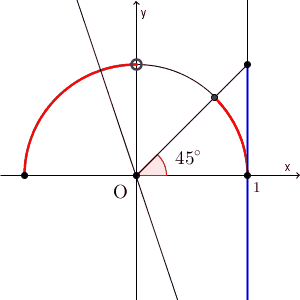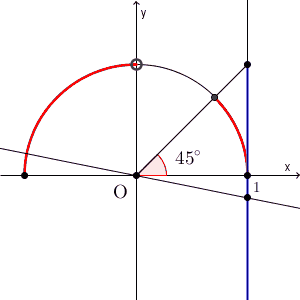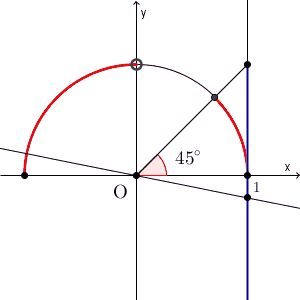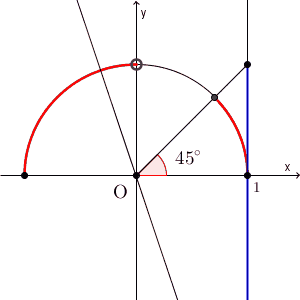
$\displaystyle \tan\theta = 1$ を満たす $\theta$ は、 $45^{\circ}$ です。この角度以下の場合と、90度より大きい場合が条件を満たすので、\[ 0^{\circ} \leqq \theta \leqq 45^{\circ}, 90^{\circ} \lt \theta \leqq 180^{\circ} \]が解となります。2つとも答えないといけません。また、 $\tan 90^{\circ}$ は定義されないので、除外して答えないといけません。