【標準】三角形とベクトルの演算

🕒 2017/08/14 🔄 2023/05/01

ここでは、三角形を使って、ベクトルの演算の練習をしていきます。

📘 目次

三角形の辺の中点とベクトル

次のような、三角形 ABC と、各辺の中点 P, Q, R を考えます。

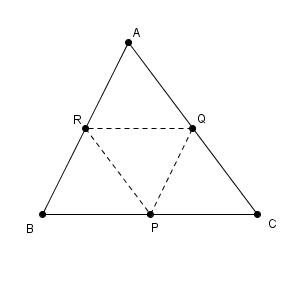
$\overrightarrow{ \mathrm{ AB } }=\vec{b}$, $\overrightarrow{ \mathrm{ AC } }=\vec{c}$ として、 $\overrightarrow{ \mathrm{ AP } }$ などを、 $\vec{b}$, $\vec{c}$ で表してみましょう。

まず、 R が線分 AB の中点であることから\[ \overrightarrow{ \mathrm{ AR } }=\frac{1}{2}\vec{b} \]であることがわかります。同じ向きで長さが半分だからですね。【基本】ベクトルの定数倍の内容を使っています。また、\[ \overrightarrow{ \mathrm{ AQ } }=\frac{1}{2}\vec{c} \]となることもわかります。

続いて、 $\overrightarrow{ \mathrm{ AP } }$ について考えてみましょう。三角形 RBP と三角形 ABC は相似なので、 RP と AC は平行です。また、 QP と AB も平行です。なので、四角形 ARPQ は平行四辺形になります。 AP はこの平行四辺形の対角線なので、
\begin{eqnarray} \overrightarrow{ \mathrm{ AP } } &=& \overrightarrow{ \mathrm{ AR } }+\overrightarrow{ \mathrm{ AQ } } \\[5pt] &=& \frac{\vec{b}+\vec{c} }{2} \\[5pt] \end{eqnarray}と表すことができます。

また、 $\overrightarrow{ \mathrm{ AP } }$ を $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ BP } }$ に分解する、という考え方もあるでしょう。\[ \overrightarrow{ \mathrm{ BC } }=\overrightarrow{ \mathrm{ AC } }-\overrightarrow{ \mathrm{ AB } }=\vec{c}-\vec{b} \]で、 BP が BC の半分であることを使えば
\begin{eqnarray} \overrightarrow{ \mathrm{ AP } } &=& \overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BP } } \\[5pt] &=& \vec{b} +\frac{1}{2} \left(\vec{c}-\vec{b}\right) \\[5pt] &=& \frac{\vec{b}+\vec{c} }{2} \\[5pt] \end{eqnarray}となります。

分解の仕方を変えても、 $\vec{b}$, $\vec{c}$ で表した式は同じになっていますね。これは、【基本】ベクトルの分解で見たように、「平行でない2つのベクトルで分解したときの表し方は1通り」であることが成り立つからなんですね。なので、例えば、 $\overrightarrow{ \mathrm{ AC } }$ と $\overrightarrow{ \mathrm{ CP } }$ というように分解しても、同じ答えになります。

分解の仕方を変えて表し方が変わるのであれば、答えが何通りにもなってしまいますよね。【基本】ベクトルの分解で見た内容は、答えは1通りになる、ということを保証してくれているので、重要なんですね。

三角形の重心とベクトル

先ほどの三角形で、重心を G とおいたとき、 $\overrightarrow{ \mathrm{ AG } }$ を $\vec{b}$, $\vec{c}$ で表してみましょう。

【基本】三角形の重心で見たように、重心は中線を $2:1$ に分割します。つまり、 $\mathrm{ AG }:\mathrm{ GP }=2:1$ です。なので、
\begin{eqnarray} \overrightarrow{ \mathrm{ AG } } &=& \frac{2}{2+1} \overrightarrow{ \mathrm{ AP } } \\[5pt] &=& \frac{\vec{b}+\vec{c} }{3} \\[5pt] \end{eqnarray}と表すことができます。

これであっているのですが、この式に少し違和感を覚える人もいるかもしれません。 $\overrightarrow{ \mathrm{ AP } }$ のときは2つを足して2で割りましたが、 $\overrightarrow{ \mathrm{ AG } }$ は2つを足して3で割っています。この気持ち悪さは、すべてのベクトルの出発点を A にしているために起こっています。将来、位置ベクトルを学んだときに、この気持ち悪さが解消するでしょう（参考：【基本】三角形の重心の位置ベクトル）。