【標準】三垂線の定理

ここでは、三垂線の定理と呼ばれている定理を証明していきます。

例題

どれも似たような内容でまぎらわしいですね。まずは、(1)の状況を図にしてみます。

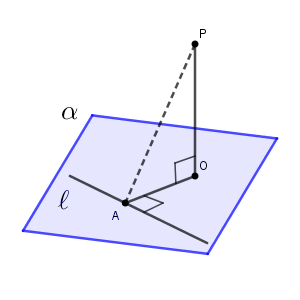
目標は、 $\mathrm{PA}\perp\ell$ です。 $\ell$ に関する条件はありますが、 $\mathrm{PA}$ については何もわかってないですね。何もわかっていないのにどうやって示すんでしょうか。

$\mathrm{PA}$ だけを眺めていてもダメです。視野を広げて、 $\mathrm{PA}$ は平面 $\mathrm{AOP}$ 上の直線だ、と考えます。すると、 $\ell$ と平面 $\mathrm{AOP}$ が垂直だと言えればよさそうです。

平面 $\mathrm{AOP}$ 上の直線には $\mathrm{PO,OA}$ があり、これらは条件にあるので使えそうです。これらをもとに証明を書いていきます。

まず、 $\mathrm{PO}\perp\alpha$ より、 $\mathrm{PO}\perp\mathrm{\ell}$ がいえます。また、条件より、 $\mathrm{OA}\perp\ell$ です。

$\ell$ は平面 $\mathrm{AOP}$ 上の平行でない2直線 $\mathrm{PO,OA}$ と垂直なので、 $\ell$ と平面 $\mathrm{AOP}$ は垂直だといえます（参考：【基本】空間における直線と平面の位置関係）。こうして、 $\mathrm{PA}\perp\ell$ がいえました。

リンク先にもある、「直線が平面と垂直であることをいうために、その平面上の平行でない2直線と垂直であることがいえればいい」ということがかなり効いています。例題の他の2つもこれを利用します。

例題の2

次に(2)を考えます。

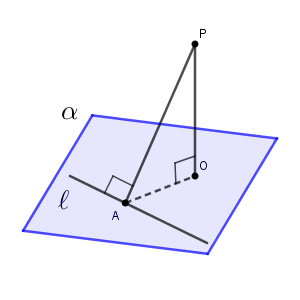
今度の目標は、 $\mathrm{OA}\perp\ell$ です。(1)と見比べると、同じような流れで証明できることがわかるでしょう。

$\mathrm{PO}\perp\alpha$ より、 $\mathrm{PO}\perp\mathrm{\ell}$ がいえます。また、条件より、 $\mathrm{PA}\perp\ell$ です。

$\ell$ は平面 $\mathrm{AOP}$ 上の平行でない2直線 $\mathrm{PO,PA}$ と垂直なので、 $\ell$ と平面 $\mathrm{AOP}$ は垂直だといえます。こうして、 $\mathrm{OA}\perp\ell$ がいえました。

例題の3

最後の(3)です。

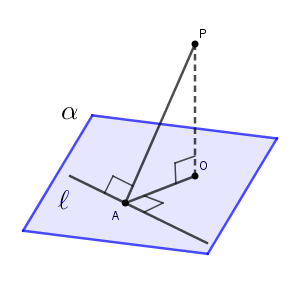
これは(1)(2)とはまた少し違った内容ですね。目標は $\mathrm{PO}\perp\alpha$ なので、 $\mathrm{PO}$ が $\alpha$ 上の2直線と垂直ということを示せないか考えてみます。

条件の一番最後から、 $\mathrm{PO\perp OA}$ が使えます。他に $\mathrm{PO}$ と垂直っぽいものを探すと、 $\ell$ しかなさそうです。これらを踏まえて証明を書いてみます。

条件より $\ell$ は、平面 $\mathrm{AOP}$ 上にある平行でない2直線 $\mathrm{PA,OA}$ と垂直なので、平面 $\mathrm{AOP}$ とも垂直だとわかります。よって、 $\mathrm{PO}\perp\ell$ がいえます。

また、最後の条件より $\mathrm{PO\perp OA}$ です。こうして、 $\mathrm{PO}$ は $\alpha$ 上の平行でない2直線 $\mathrm{OA},\ell$ と垂直だから、 $\mathrm{PO}\perp\alpha$ がいえます。

三垂線の定理

この例題で示した内容は、三垂線の定理と呼ばれています。「定理」とついているものの、覚えにくい上、利用できる場面が少ない（大学入試でほぼ出ない）ので、特に覚えておく必要はないでしょう。

それよりも、証明で何度も使った手法を理解しておく方が大事です。【基本】空間における直線と平面の位置関係で見たように、「直線が平面と垂直であることをいうために、その平面上の平行でない2直線と垂直であることがいえればいい」という内容を使いました。特に証明の中では、次のような使い方をしています。

「直線 $\ell$ が三角形 $\mathrm{ABC}$ のうちの2つの辺と垂直なら、残りの辺とも垂直である。」

直線が平面と垂直であることをいうために、平面上の2直線を考えるようにしましょう。

おわりに

ここでは、三垂線の定理についてみてきました。内容よりも、証明の中で使った、直線と平面が垂直であることを示す方法をマスターするようにしましょう。