【応用】平面に垂直な直線

🕒 2023/09/20 🔄 2023/09/25

空間において、「直線が平面に垂直」であるとは、その平面上のどんな直線とも垂直であるときをいいます。定義通りにチェックするなら、ぜんぶチェックしないといけませんが、実際には、2つだけチェックすればいいです。ここでは、そのことを証明していきます。

📘 目次

「直線が平面に垂直」を示すには

ここでは、「直線が平面に垂直であること」に関連して、次のことを示します。

直線が平面に垂直であることの十分条件

直線 $\ell$ と平面 $\alpha$ とが点 $\mathrm{O}$ で交わっているとする。点 $\mathrm{O}$ を通る平面 $\alpha$ 上の異なる2直線 $m_1,m_2$ に対し、 $\ell\perp m_1$, $\ell\perp m_2$ とする。このとき、点 $\mathrm{O}$ を通る平面 $\alpha$ 上の直線 $n$ についても、 $\ell\perp n$ が成り立つ。

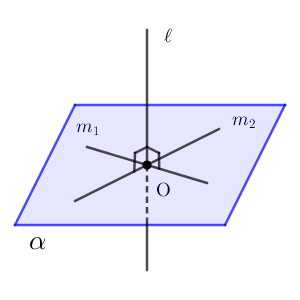
これを使えば、$\ell$ と平面 $\alpha$ が垂直であることを示すには、平面 $\alpha$ 上の（平行でない）2直線と $\ell$ とが垂直であることを示せばいいことがわかります。より正確には、平行移動によって角の大きさが変わらないことを示す必要がありますが、その点は【応用】空間における2直線のなす角で示すことにします。

さて、以下ではこの内容を示していきます。

まずは、いろいろと点の名前などを設定していきます。

直線 $m_1$ 上に、$\mathrm{OA}=\mathrm{OB}$ となるように異なる2点 $\mathrm{A,B}$ をとります。また、直線 $m_2$ 上に、$\mathrm{OC}=\mathrm{OD}$ となるように異なる2点 $\mathrm{C,D}$ をとります。

このとき、平面 $\alpha$ 上にあり、点 $\mathrm{O}$ を通る直線 $n$ が、 $\ell$ と垂直であることを示します。

直線 $n$ が線分 $\mathrm{AC,BD}$ と交わらない場合は、 $\mathrm{C,D}$ を入れ替え、線分 $\mathrm{AC,BD}$ と交わるようにして、交点を $\mathrm{E,F}$ とおきます。

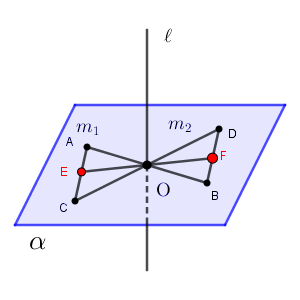
（ここまでは、扱いやすいように点に名前をつけただけです。証明の本番はここからです）

$\triangle \mathrm{OAC}\equiv \triangle \mathrm{OBD}$ （2組の辺とその間の角がそれぞれ等しいから）なので、 $\angle \mathrm{OAC}=\angle \mathrm{OBD}$ です。よって、$\triangle \mathrm{OAE}\equiv \triangle \mathrm{OBF}$ が成り立ちます（1組の辺とその両端の角がそれぞれ等しい）。こうして、 $\mathrm{AE=BF, OE=OF}$ が得られます。

直線 $\ell$ 上に $\mathrm{O}$ と異なる点 $\mathrm{G}$ をとります。

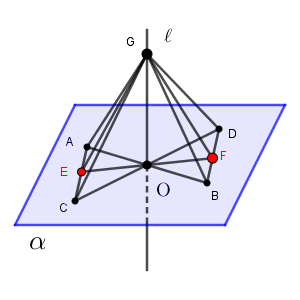
このとき、$\triangle \mathrm{GOA}\equiv \triangle \mathrm{GOB}$ が成り立つ（$\angle \mathrm{GOA}=\angle \mathrm{GOB}=90^{\circ}$ より、2組の辺とその間の角がそれぞれ等しいから）ので、 $\mathrm{GA=GB}$ となります。同様に $\mathrm{GC=GD}$ も成り立ちます。

よって、 $\triangle \mathrm{GAC}\equiv\triangle \mathrm{GBD}$ （3組の辺がそれぞれ等しいから）となるので、 $\angle \mathrm{GAC}=\angle\mathrm{GBD}$ となります。これより、 $\triangle \mathrm{GAE}\equiv\triangle \mathrm{GBF}$ （2組の辺とその間の角がそれぞれ等しいから）なので、 $\mathrm{GE=GF}$ が成り立ちます。よって、 $\triangle \mathrm{GOE}\equiv\triangle \mathrm{GOF}$ である（3組の辺がそれぞれ等しい）から、 $\angle \mathrm{GOE}=90^{\circ}$ となることがいえます。

こうして、直線 $\ell$ と直線 $\mathrm{EF}$ が垂直であること、つまり、 $\ell\perp n$ が示せました。これで証明終わりです。