【標準】連立一次不等式

方程式の次に連立方程式が出てきたように、不等式の次には連立不等式が出てきます。日常でも、「この金額を○円から△円の間にしたい」という場合があります。このように、2つの不等式を同時に満たすものをこの記事では考えていきます。

例題1

連立一次不等式とは、複数の一次不等式を組み合わせたものをいいます。「連立一次不等式を解きなさい」と言われた場合は、すべての不等式を満たす範囲を答えることになります。

次の例題を見てみましょう。

それぞれの不等式を解いて、最後に共通範囲を求める、という順番になります。

まず、1つ目の不等式は次のように解けます。
\begin{eqnarray} 2x -9 & \gt & -13 \\ 2x & \gt & -4 \\ x & \gt & -2 \\ \end{eqnarray}2つ目の不等式は次のように解けます。 \begin{eqnarray} -x+5 & \geqq & 3 \\ -x & \geqq & -2 \\ x & \leqq & 2 \\ \end{eqnarray} 最後に、2つの範囲をまとめるのですが、それぞれの範囲がどうなっているか、数直線で考えたほうがわかりやすいです（【基本】一次不等式の解と数直線で出てきた考え方です）。

2つの範囲を図示すると、次のようになります。

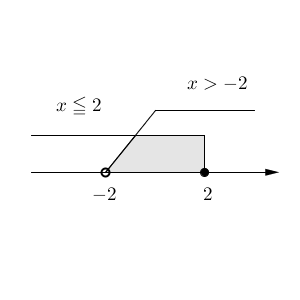
両方に含まれる範囲が答えなので、$-2 \lt x \leqq 2$ が求める答えになることが分かります。

例題2

少し形は違いますが、次も連立一次方程式の一種です。

これは1つにつながっていますが、 $0 \lt x+1$ と $x+1 \lt -2x+7$ という2つの不等式から成り立っています。なので、連立一次方程式です。解き方は先ほどと同じで、それぞれの不等式を解いて、その共通範囲を求める、という手順です。

まず、$0 \lt x+1$ からは、$x\gt -1$ が得られます。また、 $x+1 \lt -2x+7$ を解くと
\begin{eqnarray} x+1 & \lt & -2x+7 \\ 3x & \lt & 6 \\ x & \lt & 2 \\ \end{eqnarray}が得られます。先ほどと同じように数直線を書いて考えれば、 $-1 \lt x \lt 2$ が解になることが分かります。

おわりに

連立一次方程式は、一次不等式が複数組み合わさったものであり、それぞれの不等式の解の共通部分を求めればいいことを見てきました。また、共通部分を考えるには、数直線を使った方がわかりやすいことも見てきました。

今回解いたのは基本的なものなので、しっかりと解けるようにしておきましょう。なお、連立一次方程式は、解が少し変わったものになるケースがあります。そういった特殊な場合は、また別途取り上げることにします（参考：【応用】連立一次不等式（変な解））。