【標準】絶対値と領域

ここでは、領域を求める問題で、不等式に絶対値が入っていた場合を考えます。

絶対値と領域

不等式の $|x+y|$ の部分に絶対値がついています。絶対値とは、中身が0以上ならそのまま、負ならマイナスをつけた数字を表すものです（参考：【基本】絶対値）。

絶対値は、そのままでは扱いにくいので、普通は、場合分けをして絶対値を外します（参考：【標準】絶対値を含む一次不等式（場合分け））。ここでも、場合分けで考えていきます。

まず、 $x+y \geqq 0$ 、つまり、 $y\geqq -x$ の場合を考えましょう。このとき、絶対値はそのまま外れるので、元の不等式は
\begin{eqnarray} x+y & \leqq & 1 \\[5pt] y & \leqq & -x+1 \end{eqnarray}となります。よって、場合分けの条件とあわせて、\[ -x \leqq y \leqq -x+1 \]となります。

続いて、 $x+y \lt 0$ 、つまり、 $y\lt -x$ の場合を考えましょう。このとき、絶対値はマイナスをつけて外すことになるので、不等式は
\begin{eqnarray} -(x+y) & \leqq & 1 \\[5pt] x+y & \geqq & -1 \\[5pt] y & \geqq & -x-1 \\[5pt] \end{eqnarray}となります。よって、場合分けの条件と合わせて、\[ -x-1 \leqq y \lt -x \]となります。

2つの領域が出てきました。この2つの領域は、 $x+y$ が0以上のときと負のときで分けたことによって出てきたものなので、これらをくっつけたものが、求める領域となります。

1つ目の領域 $-x \leqq y \leqq -x+1$ は次のようになります（境界線上の点を含む）。

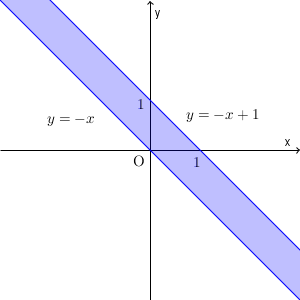
2つ目の領域 $-x-1 \leqq y \lt -x$ は次のようになります。片方には等号が入ってないことに注意しましょう。境界線上の点は $y=-x$ 上の点は含まず、 $y=-x-1$ 上の点は含みます。

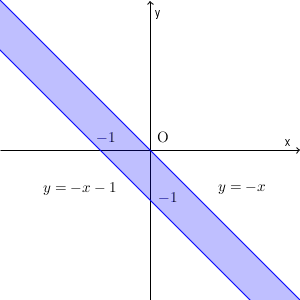
「 $y=-x$ の上の点は含まない」と言いましたが、ここは1つ目の領域との境目にもなっています。1つ目の領域では、 $y=-x$ 上の点を含みます。そのため、2つの領域を合わせれば、 $y=-x$ の境界線はうまく消えます。

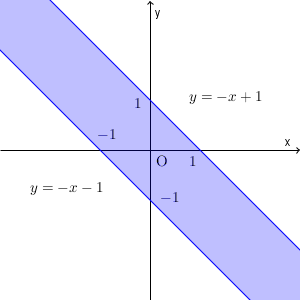
結果として、求める領域は上の色の部分（境界線上の点を含む）となります。

絶対値が複数ある場合も、基本的に場合分けをして絶対値を外して考えます。場合分けの条件と合わせた範囲を考えるので、【基本】連立不等式と領域の内容が役に立つでしょう。

おわりに

ここでは、絶対値を含んだ不等式が表す領域について考えました。基本的には、場合分けをして絶対値を外して考えます。場合分けをすると式が増え、さらに境界線のことも気にしないといけないので、ごちゃごちゃしやすくなります。何を計算しているかを意識して考えるようにしましょう。