🏠 Home / 数学II / 微分と積分の基礎 / 微分と三次関数のグラフ

【標準】四次関数と微分

🕒 2017/10/25 🔄 2023/05/01

ここでは、微分を使って、四次関数のグラフの例をいくつか見ていきます。

📘 目次

四次関数と微分その１

例題1

次の関数の極値を求め、グラフの概形をかきなさい。\[ y=x^4-2x^2+2 \]

四次関数になっても、三次関数のときと流れは同じです。微分をして導関数の符号を調べ、増減表をかいていきます。

微分した結果はこうなります。\[ y'=4x^3-4x=4x(x-1)(x+1) \]次に、導関数の符号を調べます。導関数は三次関数ですが、このグラフをまじめにかく必要はありません。符号が分かればそれで十分だからです。

符号が変わる境目の候補は、 $y'=0$ のときなので、 $x=-1,0,1$ の3ヶ所ですね。導関数は、これらを境目として、負⇒正⇒負⇒正、と符号が切り替わっていきます。そのため、増減表は次のようになります。
\begin{array}{c|ccccccc} x & \cdots & -1 & \cdots & 0 & \cdots & 1 & \cdots \\ \hline y' & - & 0 & + & 0 & - & 0 & + \\ \hline y & \searrow & 1 & \nearrow & 2 & \searrow & 1 & \nearrow \end{array}これから、 $x=-1$ で極小値 $1$ 、 $x=0$ で極大値 $2$ 、 $x=1$ で極小値 $1$ をとることがわかります。このように、極小値が2か所のこともあります。

これをもとにグラフをかけば、次のようになります。

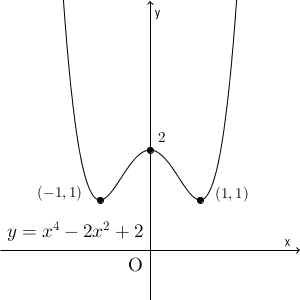
山が1つ、谷が2つ。三次関数のグラフとはまた違った形ですね。

四次関数と微分その２

例題2

次の関数の極値を求め、グラフの概形をかきなさい。\[ y=3x^4+4x^3+1 \]

これも、微分をして導関数の符号を調べましょう。微分をすると\[ y'=12x^3+12x^2=12x^2(x+1) \]となります。よって、 $y'=0$ となるときは、 $x=-1,0$ のとき、となります。

導関数にある $x^2$ の部分はつねに $0$ 以上ですね。よって、導関数の符号が変わるのは $x=-1$ の前後だけであることがわかります。よって、増減表は次のようになります。
\begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 0 & \cdots \\ \hline y' & - & 0 & + & 0 & + \\ \hline y & \searrow & 0 & \nearrow & 1 & \nearrow \end{array}これから、 $x=-1$ で極小値 $0$ をとることがわかります。 $x=0$ の前後では導関数の符号が変わらないため、ここでは極値をとりません。

このことから、グラフは次のようになります。

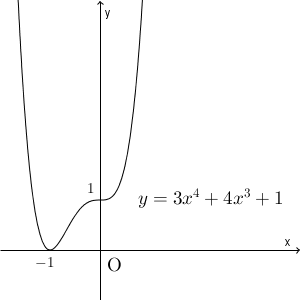
これもまた変わった形ですね。山がなく、谷が1つだけ、という形です。

一次関数のグラフは直線で、二次関数のグラフは放物線でした。どんな形になるかは決まっていました。しかし、三次関数のグラフになると、山と谷が両方あったり両方なかったりします（参考：【標準】三次関数と微分）。四次関数になると、山と谷が両方あるケースもあり、片方だけあるケースもありました。

三次以上になるとパターンが増えるため、「このときはこうなる」というルールを1つ1つ調べていくときりがありません。しかし、微分を使えば、三次以上の場合でも、導関数の符号が変わるときに注目し、これをもとにすれば関数の増減がわかり、グラフをかくことができます。つまり、すべての場合を事前に見ておくのではなく、どんな関数が来ても対応できるツールで対処していく、ということなんですね。そのためのツールが「微分」です。