【標準】絶対値記号を含む二次不等式
ここでは、絶対値を含む二次不等式を、グラフを用いて解く方法を見ていきます。
絶対値記号を含む二次不等式
式だけで解くこともできますが、ここではグラフを用いて考えることにしましょう。
$y=|x^2-3x|$ と $y=x$ のグラフをかいて、1つ目のほうが上、または、同じ、となっている範囲を考えます。
$y=|x^2-3x|$ のグラフは、 $y=x^2-3x$ のグラフで、 $x$ 軸より下の部分を折り返したものになります。なので、次のようになります。

$x$ の値で場合分けをして考えても構いません。
次に、 $y=x$ のグラフを追加します。このとき、交点がどうなるかを考えましょう。
$y=x^2-3x$ と $y=x$ の交点の $x$ 座標は、
\begin{eqnarray}
x^2-3x &=& x \\[5pt]
x(x-4) &=& 0 \\[5pt]
x &=& 0,4 \\[5pt]
\end{eqnarray}となります。また、 $y=-x^2+3x$ と $y=x$ の交点の $x$ 座標は、
\begin{eqnarray}
-x^2+3x &=& x \\[5pt]
-x(x-2) &=& 0 \\[5pt]
x &=& 0,2 \\[5pt]
\end{eqnarray}となります。
以上から、先ほどのグラフに $y=x$ を追加すると次のようになります。

これを見れば、 $y=|x^2-3x|$ のグラフのうち、 $|x^2-3x|\geqq x$ を満たすのは、以下の赤い線の部分になります(端点も含む)。
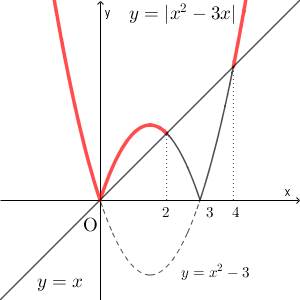
よって、 $x\leqq 2$, $x\geqq 4$ となります。
ちなみにその1
ちなみに、この例題がこのようになっていたら、この答えはどう変わるでしょうか。
「先ほどの答えからイコールをはずせばいいのかな?」と思うかもしれません。しかし、グラフをよく見ると、それではダメなことがわかります。 $y=|x^2-3x|$ のグラフのうち、 $|x^2-3x|\gt x$ を満たすのは、以下の赤い線の部分になります。
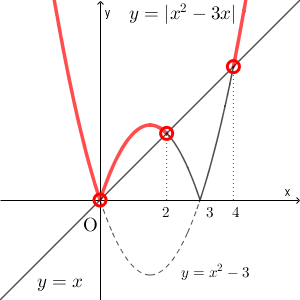
$y=|x^2-3x|$ のグラフが $y=x$ のグラフより上にある範囲が答えなので、 $x=0$ は外さなくてはいけません。つまり、答えは次のようになります。
$x\lt 0$, $0\lt x\lt 2$, $x\gt 4$
イコールを抜いて終わり、ではありません。グラフを見て考えましょう。
ちなみにその2
もとの例題を、式をメインにして解いてみます。
$x^2-3x=x(x-3)$ なので、 $x^2-3x$ は $x\leqq 0$, $x\geqq 3$ のときは0以上、 $0\lt x\lt 3$ のときは負となります。
$x\leqq 0$, $x\geqq 3$ のときは
\begin{eqnarray}
x^2-3x \geqq x \\[5pt]
x^2-4x \geqq 0 \\[5pt]
x(x-4) \geqq 0 \\[5pt]
\end{eqnarray}なので、 $x\leqq 0$, $x\geqq 4$ となります。これらの範囲は、今考えている範囲に含まれます。
$0\lt x \lt 3$ のときは
\begin{eqnarray}
-x^2+3x \geqq x \\[5pt]
x^2-2x \leqq 0 \\[5pt]
x(x-2) \leqq 0 \\[5pt]
\end{eqnarray}なので、 $0\leqq x\leqq 2$ となります。今考えている範囲では、 $0\lt x\leqq 2$ となります。
以上を合わせると、 $x\leqq 2$, $x\geqq 4$ となります。これが答えです。
$y=|x^2-3x|$ のグラフを用いなくても解くことは可能ですが、グラフを用いて視覚的に解いたほうが間違いに気づきやすくなります。
おわりに
ここでは、絶対値を含む二次不等式の問題を見てきました。グラフを用いずに解くこともできますが、グラフをかいて視覚的に解くと間違っていたときに気づきやすくなります。





