【標準】すべての実数で成り立つ二次不等式

ここでは、すべての実数で成り立つ二次不等式について考えます。

二次不等式の解が実数全体になる場合は、【基本】二次不等式（判別式が負のとき）や【基本】二次不等式（判別式が0のとき）で出てきました。ここでは、逆に、二次不等式の解が実数全体になるような条件を求める問題を見ていきます。

例題

すべての実数で $x^2+mx+2m-3\gt 0$ が成り立つということは、放物線 $y=x^2+mx+2m-3$ が x 軸より上にある、ということですね。つまり、 x 軸との交点がない場合なので、二次方程式 $x^2+mx+2m-3=0$ が実数解を持たないときであることがわかります。

このとき、この二次方程式の判別式を D とすると、 $D\lt 0$ が成り立つということなので、
\begin{eqnarray} m^2-4(2m-3) \lt 0 \\ m^2-8m+12 \lt 0 \\ (m-2)(m-6) \lt 0 \\ \end{eqnarray}このことから、 $2\lt m \lt 6$ が解になることが分かります。

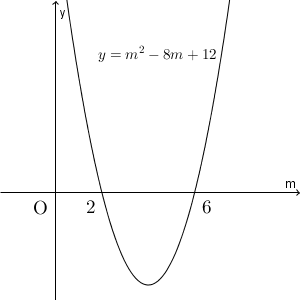
これは、【標準】二次方程式が実数解を持つ範囲と同じグラフです。「すべての実数で二次不等式が成り立つ」を「二次方程式が実数解を持たない」に言い換えられるかどうか、がこの問題のポイントです。言い換えることができれば、あとは解の個数を調べるために判別式を使うだけです。

いろいろなパターン

ちなみに、上の例題が「二次不等式 $x^2+mx+2m-3\geqq 0$ の解がすべての実数であるとき」であれば、放物線が x 軸上か、それより上ならいいので、 x 軸との共有点の個数は1個以下、つまり、「 $D\leqq 0$ 」という条件を考えればいいことが分かります。

また、「二次不等式 $x^2+mx+2m-3\lt 0$ の解がすべての実数であるとき」というのは起こりえません。下に凸の場合、グラフ全体が x 軸の下にあることはないからです。

なお、上の例題を解くにあたり、「二次関数 $y=x^2+mx+2m-3$ の最小値が $0$ より大きいとき」を求めればいい、と考えることもできます。平方完成をして、頂点の y 座標が正である範囲を考えても、同じ答えになります。