【標準】二次関数と微分

🕒 2017/10/23 🔄 2023/05/01

ここでは、微分の考えを使って、二次関数のグラフについて再度考えてみることにします。すでに知っているものを再考するため、新しく問題が解けるようになるということはありませんが、微分の考えをより深めるために役立つと思います。

📘 目次

二次関数と微分

【基本】増減表で見たように、導関数（微分をして得られる関数）の符号を調べることで、グラフをかくことができます。そのため、微分を使えば、三次関数のグラフもかけるようになります。

ここでは、その微分を使って、あえて、二次関数のグラフを考えてみます。二次関数のグラフがどうなるかはすでに知っているはずですが、微分を使えば、どういうことがわかるかを見てみます。

一般的な話をしていくため、 $y=ax^2+bx+c$ という二次関数について考えてみましょう。まずは、 $a\gt 0$ として、話を進めていきます。

これを微分すると、次のようになります。\[ y'=2ax+b \]$a\gt 0$ の場合、 x がすごく小さい値であれば $y'$ は負で、 x が大きな値をとれば $y'$ は正になります。その境目は、 $y'=0$ となるときであり、 $x=-\dfrac{b}{2a}$ のときですね。これらのことから、この二次関数の増減表は、次のようになります。
\begin{array}{c|ccccc} x & \cdots & -\frac{b}{2a} & \cdots \\ \hline y' & - & 0 & + \\ \hline y & \searrow & & \nearrow \end{array}この増減表から、この二次関数のグラフは、途中まで右肩下がり、途中から右肩上がりになる、ということがわかります。この切り替わるところを「極小」というのでしたね（参考：【基本】極大値と極小値）。

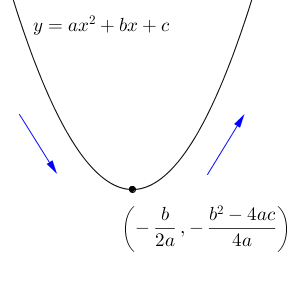
ところで、この極小値をとる点の座標に見覚えはありませんか？　これは、【標準】二次関数y=ax^2+bx+cのグラフの頂点でも見た通り、放物線の頂点の座標なんですね。放物線の頂点を求めるには、次のように平方完成して計算するのでした。
\begin{eqnarray} y &=& ax^2+bx+c \\[5pt] &=& a\left(x^2+\frac{b}{a}x\right)+c \\[5pt] &=& a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}+c \\[5pt] &=& a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a} \\[5pt] \end{eqnarray}これから、頂点の座標は\[ \left(-\frac{b}{2a},-\frac{b^2-4ac}{4a}\right) \]と求められます。

二次関数 $y=ax^2+bx+c \ (a\gt 0)$ の谷底の部分は、二次関数の世界では「頂点」と言っていましたが、これを微分の世界では「極小」と呼ぶ、ということなんですね。頂点を求めるには上のように平方完成をする必要がありますが、微分の世界では $y'=2ax+b$ が $0$ になる場所、と考えます。違うアプローチですが、同じ結果にたどりつきます。

なお、 $a\lt 0$ のときは、導関数の符号が反転するため、はじめは右肩上がりで途中から右肩下がりになります。切り替わる点の座標は上の計算と同じなので、頂点で極大になることもわかります。