【標準】二次曲線の平行移動
ここでは、放物線、楕円、双曲線を、平行移動した場合に、方程式がどう変わるかを見ていきます。
楕円の平行移動
楕円 $\dfrac{x^2}{4}+y^2=1$ を平行移動することを考えましょう。原点が中心となる場合以外も扱えた方がいいですからね。
この楕円を x 軸方向に $2$, y 軸方向に $1$ だけ平行移動したとき、平行移動後の楕円の方程式はどうなるでしょうか。
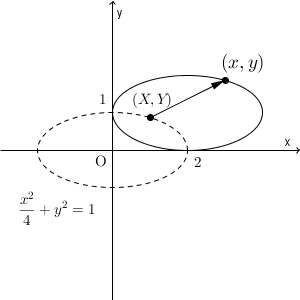
「2つの焦点からの距離の和が等しい点を求める」という方法もありますが、計算が面倒すぎます。それよりも、平行移動前の方程式がわかっているので、これを利用することを考えましょう。
もとの楕円の上にある点 $(X,Y)$ が、平行移動後に $(x,y)$ に移動するとしましょう。知りたいのは、 $(x,y)$ が満たす関係式です。平行移動の情報から\[ X+2=x,\ Y+1=y \]となることから、\[ X=x-2,\ Y=y-1 \]となることがわかります。
また、 $(X,Y)$ は平行移動前の楕円の上の点なので、\[ \dfrac{X^2}{4}+Y^2=1 \]を満たします。よって、これにさきほどの関係式を入れれば\[ \dfrac{(x-2)^2}{4}+(y-1)^2=1 \]となります。これは、平行移動後の点 $(x,y)$ が満たす式なので、これが平行移動後の楕円の方程式、となります。
もし焦点の座標も求めたい場合は、平行移動前の状態で求めてから、点の平行移動として考えたほうが求めやすいでしょう。今の例であれば、平行移動前の楕円の焦点は $(\sqrt{3},0)$, $(-\sqrt{3},0)$ なので、平行移動後の楕円の焦点は、 $(2+\sqrt{3},1)$, $(2-\sqrt{3},1)$ となります。
放物線の平行移動
放物線の移動も、楕円のときと考え方は同じです。「平行移動前の式」を利用します。
放物線 $y^2=x$ を、 x 軸方向に $-1$, y 軸方向に $2$ だけ平行移動して得られる放物線の方程式を考えましょう。
これも、点 $(X,Y)$ が $(x,y)$ に移動するとします。このとき、\[ X=x+1,\ Y=y-2 \]が成り立ちます。これを、もとの放物線の方程式に入れれば\[ (y-2)^2=x+1 \]となります。これが平行移動後の放物線の方程式です。
双曲線のときも、考え方は同じです。
平行移動後の曲線の方程式
一般に、 $x,y$ の方程式 $F(x,y)=0$ が与えられていたとします。 $F(x,y)$ とは、 $x,y$ の関数のことで、上で見た楕円や放物線、双曲線は、この形で書くことができます。ひとつ目の楕円の例であれば\[ F(x,y)=\dfrac{x^2}{4}+y^2-1 \]ということですね。
この $F(x,y)=0$ を満たす点全体がある曲線を表すとき、その曲線のことを「曲線 $F(x,y)=0$ 」といいます。
これを、 x 軸方向に p, y 軸方向に q だけ平行した後の曲線の方程式を考えましょう。
これは、上で考えたことを一般化しているだけです。平行移動により、 $(X,Y)$ が $(x,y)$ に移動したとすると、\[
X=x-p,\ Y=y-q \]が成り立ちます。また、 $F(X,Y)=0$ が成り立つことから、平行移動後の点 $(x,y)$ は\[ F(x-p,y-q)=0 \]を満たします。これが平行移動後の曲線の方程式となります。
F(x-p,y-q)=0 \]
ちょっと抽象的ですが、つまり、 $x,y$ を $x-p,y-q$ で置き換えれば、移動後の曲線の方程式が得られる、ということです。符号がマイナスになっていることに注意しましょう。
かつての二次関数の平行移動
昔、二次関数を学んだときにも、このグラフの平行移動の話は出てきています。【基本】二次関数y=a(x-p)^2+qのグラフや【発展】グラフの平行移動などです。
このときは、放物線 $y=a(x-p)^2+q$ は、放物線 $y=ax^2$ を x 軸方向に p, y 軸方向に q だけ平行したものだ、ということを見ました。頂点の移動に着目すれば、たしかにそうなることが理解できるでしょう。
先ほど見た内容にこのことをあてはめるなら、\[ F(x,y)=y-ax^2 \]のときに対応しています。平行移動後の放物線は $F(x-p,y-q)=0$ 、つまり、\[ (y-q)-a(x-p)^2=0 \]となり、式変形をすれば $y=a(x-p)^2+q$ となります。
最後の式だけを見ると、 $x$ が $x-p$ となり、最後は $+q$ なので、 $p,q$ の符号が違うように見えます。しかし、先ほど見た内容を踏まえれば、 $x-p$, $y-q$ というように、両方ともマイナスになっているが、 $-q$ は移行することによって、たまたまプラスになっていた、ということがわかります。
おわりに
ここでは、楕円、放物線、双曲線の平行移動について見てきました。 $x-p$, $y-q$ とおけば求めたい式が得られる、ということをおさえておきましょう。





