【標準】比例式と恒等式の証明

🕒 2017/05/19 🔄 2023/07/13

ここでは、比例式を使った条件のついた、恒等式を証明する問題を考えていきます。

📘 目次

比例式の条件が付いた恒等式の証明問題

例題

$\dfrac{a}{b}=\dfrac{c}{d}$ のとき、次の等式が成り立つことを示しなさい。\[ \frac{a+c}{b+d}=\frac{a-c}{b-d} \]

$\dfrac{a}{b}=\dfrac{c}{d}$ といった式のことを、比例式というんでしたね（参考：【基本】比例式）。比例式が出てきたときは、比の値を「 $=k$ 」と置いて考えていくとうまくいくことが多いです。ここでも、その発想で考えていきましょう。

$\dfrac{a}{b}=k$ とおくと、 $a=bk$ となります。また、条件式より、 $c=dk$ も成り立ちます。

示すべき等式の「左辺引く右辺」に、これらを代入してみましょう。
\begin{eqnarray} & & \dfrac{a+c}{b+d} -\dfrac{a-c}{b-d} \\[5pt] &=& \dfrac{bk+dk}{b+d} -\dfrac{bk-dk}{b-d} \\[5pt] &=& \dfrac{k(b+d)}{b+d} -\dfrac{k(b-d)}{b-d} \\[5pt] &=& k-k \\[5pt] &=& 0 \end{eqnarray}となります。これから、与えられた等式が成り立つことがわかります。

イコール定数としなければどうなるか

先ほどの問題で「 $=k$ と置くとうまくいくことが多い」と書きましたが、もしこう置かなければどうなるのかを考えてみましょう。

条件式を文字を減らすために使えば、 $a=\dfrac{bc}{d}$ となります。これを示すべき等式の「左辺引く右辺」に、これらを代入すると、次のようになります。
\begin{eqnarray} & & \dfrac{a+c}{b+d} -\dfrac{a-c}{b-d} \\[5pt] &=& \dfrac{\dfrac{bc}{d}+c}{b+d} -\dfrac{\dfrac{bc}{d}-c}{b-d} \\[5pt] &=& \dfrac{bc+cd}{d(b+d)} -\dfrac{bc-cd}{d(b-d)} \\[5pt] &=& \dfrac{c(b+d)}{d(b+d)} -\dfrac{c(b-d)}{d(b-d)} \\[5pt] &=& \dfrac{c}{d}-\dfrac{c}{d} \\[5pt] &=& 0 \end{eqnarray}となります。これから、与えられた等式が成り立つことがわかります。

もちろん、このようにして証明することもできます。しかし、少し計算が面倒ですね。2つの解き方と見比べてみると、1つ目の解き方では、「比の値イコール定数」と置くことで条件式から分数を消すことができます。この分だけ、計算がしやすくなっています。

加比の理

さて、上で見た等式をもう少し詳しく見てみましょう。

\[ \dfrac{a}{b}=\dfrac{c}{d}=k \]と置きましたが、その後の計算で\[ \dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}=k \]であることもわかりました。つまり、\[ \dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d} \]が成り立つということですね。

このように、「比の値が等しければ、分子同士・分母同士を足しても値が変わらない」ことを、加比の理（かひのり）といいます。比の形で書けば、
　「$a:b=c:d$ ならば、 $(a+c):(b+d)=a:b$ が成り立つ」
ということです。

これは、図形的に考えると理解しやすいでしょう。

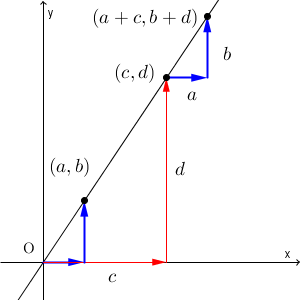
$\dfrac{a}{b}=\dfrac{c}{d}$ が成り立つということは、 $(a,b)$ と $(c,d)$ は、直線 $y=\dfrac{a}{b}x$ 上にある、ということです。 $(c,d)$ から出発して、右に $a$ 進み、上に $b$ 進めば、同じ傾きの方向に動くことになるので、動いた後も同じ直線上にあります。反対方向に進んでも同じですね。また、「 $=k$ 」と置きましたが、これは直線の傾きに対応しています。