【標準】放物線の平行移動（頂点に着目）

🕒 2016/07/17 🔄 2023/05/01

【標準】二次関数y=ax^2+bx+cのグラフ（具体例）や【標準】二次関数y=ax^2+bx+cのグラフの頂点で、二次関数のグラフのかき方、特に頂点の座標の求め方を見てきました。ここでは、このことを踏まえて、平行移動した放物線の方程式を求めたり、2つの放物線を重ねるにはどう平行移動すればいいか、という問題を考えていきます。

📘 目次

平行移動後の放物線の方程式

次の例題を考えてみます。

例題

放物線 $y=3x^2-12x+10$ を x軸方向に $1$ 、 y 軸方向に $-2$ だけ平行移動した放物線の方程式を求めなさい。

放物線を平行移動したとき、移動前と後とで「どの点とどの点が対応しているか」を見るのは難しいです。しかし、1点だけわかりやすい点があるんですね。それが頂点です。頂点は、谷の底か山の頂上なので、平行移動してもどのように移動したかがわかります。なので、頂点に着目してみましょう。

二次関数のグラフをかくときに、頂点の座標の求め方はすでに学びました（参考：二次関数y=ax^2+bx+cのグラフの頂点）。さらに、平行移動後の頂点の座標がわかれば、その放物線の方程式もわかります（参考：二次関数y=a(x-p)^2+qのグラフ）。

平行移動しても $x^2$ の係数は変わらないので、頂点がどう移動するかがわかれば解くことができます。

解答

\begin{eqnarray} y &=& 3x^2-12x+10 \\ &=& 3(x^2-4x)+10 \\ &=& 3\{(x^2-4x+4)-4\}+10 \\ &=& 3\{(x-2)^2-4\}+10 \\ &=& 3(x-2)^2-12+10 \\ &=& 3(x-2)^2-2 \\ \end{eqnarray}なので、移動前の放物線の頂点は $(2,-2)$ となる。よって、移動後の放物線の頂点は $(3,-4)$ なので、移動後の放物線の方程式は \begin{eqnarray} y &=& 3(x-3)^2-4 \\ &=& 3(x^2-6x+9)-4 \\ &=& 3x^2-18x+23 \\ \end{eqnarray}となる。（終）

放物線を平行移動する場合は、頂点の座標に着目すればOKです。

移動前の頂点を求める
移動後の頂点を求める
移動後の放物線の方程式を求める

というステップです。

どう平行移動すればいいか

続いて、次の問題を考えてみましょう。

例題

放物線 $y=-x^2+6x+2$ は、どのように平行移動すれば、放物線 $y=-x^2-2x-4$ と重なるか、答えなさい。

頂点は頂点に移動するので、これも、頂点がどう移動するかだけを考えればいいんですね。

解答

放物線 $y=-x^2+6x+2$ の頂点は
\begin{eqnarray} y &=& -x^2+6x+2 \\ &=& -(x^2-6x)+2 \\ &=& -(x^2-6x+9-9)+2 \\ &=& -(x-3)^2+9+2 \\ &=& -(x-3)^2+11 \\ \end{eqnarray}なので、 $(3,11)$ となる。
放物線 $y=-x^2-2x-4$ の頂点は
\begin{eqnarray} y &=& -x^2-2x-4 \\ &=& -(x^2+2x)-4 \\ &=& -(x^2+2x+1-1)-4 \\ &=& -(x+1)^2+1-4 \\ &=& -(x+1)^2-3 \\ \end{eqnarray}なので、 $(-1,-3)$ となる。
この2つの点が重なるように移動すればいいので、「x 軸方向に $-4$ 、y 軸方向に $-14$ だけ平行移動」すればよい。
（終）

なお、グラフは次のようになります。

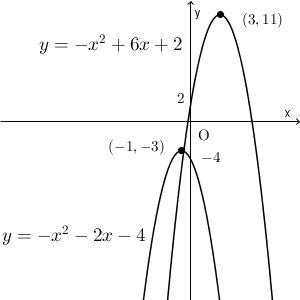
ちなみに、 $y=ax^2+bx+c$ は $y=a(x-p)^2+q$ の形に変形できるので、このグラフは $y=ax^2$ のグラフを平行移動したものだ、ということがわかります。つまり、2つの放物線の方程式があって、その $x^2$ の係数が等しければ、片方の放物線を平行移動して、もう片方と重ねることができる、ということです。