【標準】軌跡（連動して動く点）

ここでは、ある点に連動して動く点の軌跡を考えます。除かないといけない点がある場合を考えます。

連動して動く点の軌跡

そもそも、重心の座標をどうやって出すかを知っていないとできないですね。【標準】三角形の重心の座標で見た通り、重心の座標は3点の座標の平均で求められます。これを踏まえて考えていきましょう。

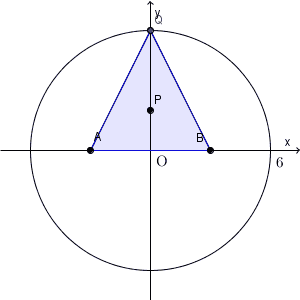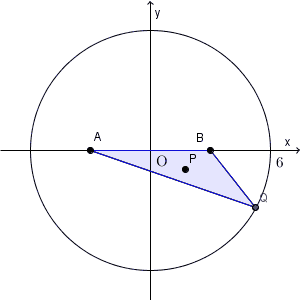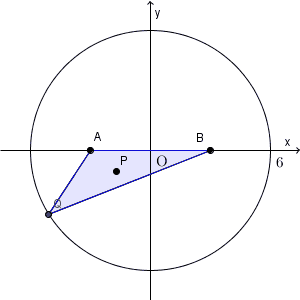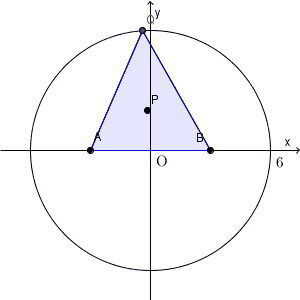
連動する点の軌跡は、【基本】軌跡（連動して動く点）でも考えましたが、まずは、元となる点 Q と 考えたい点 P との関係を見ていく必要があります。

$\mathrm{ Q }(s,t)$ とし、 $\mathrm{ P }(X,Y)$ とします。重心の座標について、\[ \left(\frac{-3+3+s}{3},\frac{0+0+t}{3}\right)=(X,Y) \]が成り立ちます。これを整理すると、\[ s=3X, t=3Y \]となります。

また、 $\mathrm{ Q }(s,t)$ は、円 $x^2+y^2=36$ 上の点なので、\[ s^2+t^2=36 \]が成り立ちます。これに先ほどの式を入れると
\begin{eqnarray} (3X)^2+(3Y)^2 &=& 36 \\[5pt] X^2+Y^2 &=& 4 \\[5pt] \end{eqnarray}となります。よって、点 P は、円 $x^2+y^2=4$ の上にあることがわかります。

答えのようなものが得られましたが、気をつけないといけないのは、これが答えではない、という点です。

除かないといけない点について

先ほど求めた「円 $x^2+y^2=4$ 」は答えではありません。ここには、除かないといけない点が含まれてしまっています。どの点を除かないといけないでしょうか。

問題文を読むと、点 P は三角形 ABQ の重心なんですね。これは、前提として、「A, B, Q をつないで、三角形ができるとき」を考えているということです。なので、三角形ができない場合は、そもそも P に関しての話はできません。このような場合は、除いて考える必要があります。

「三角形ができない場合」というのは、今の場合、 Q が x 軸上にいるときです。そのため、 $t\ne 0$ という条件が隠れています。 $Y=3t$ だったので、これに応じて「 $Y\ne 0$ 」という条件を考えないといけません。

以上から、求める軌跡は、「円 $x^2+y^2=4$ 、ただし、2点 $(-2,0),(2,0)$ を除く」となります。これが答えです。（下の図では、通ってるように見えますが。。。）

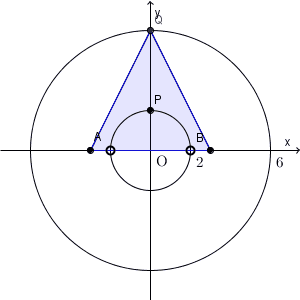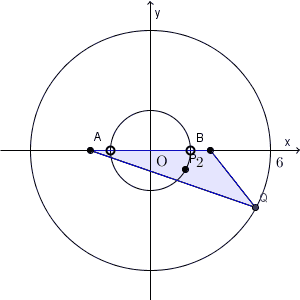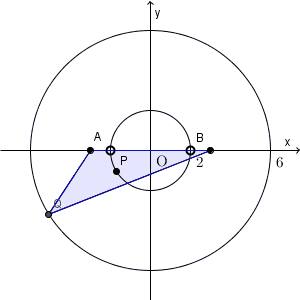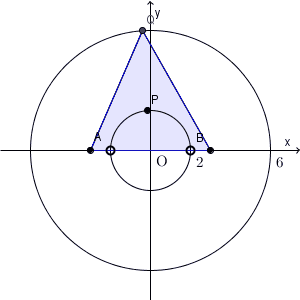
【基本】軌跡でも書きましたが、「条件を満たす点はこの図形上にある」ということだけでなく、「この図形上のすべての点は条件を満たす」ということも要求されます。不必要なものがある場合は、除いて答えないといけません。

今の場合は、「三角形 ABQ 」というのが、隠れた条件になっています。三角形が作れない場合を除く必要があります。関係式が出てそこで安心するのではなく、「すべての点が条件を満たすだろうか」ということをきちんと考える必要があります。

おわりに

ここでは、連動して動く点の軌跡を求める問題を見ました。不要な点を除いて答えないといけませんでしたね。例外ケースがわかりにくいものもあるので、いろんな問題を解いて練習しましょう。