🏠 Home / 数学I / 数と式 / 一次不等式

【標準】絶対値を含んだ一次不等式（絶対値の性質）

🕒 2016/06/13 🔄 2023/05/01

この記事では、不等式に絶対値が含まれている問題を考えます。【標準】絶対値を含む一次不等式（場合分け）では、場合分けをして絶対値を外す方法を紹介しましたが、ここでは、絶対値の性質を使う方法を紹介します。

📘 目次

絶対値の性質

絶対値は、数直線で考えると、原点からの距離を表すのでしたね。$|a|$ というのは、原点と $a$ との距離ということです。

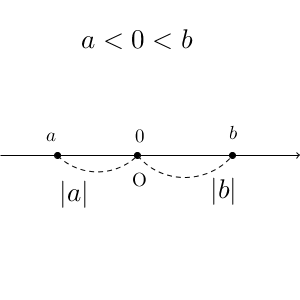
このことを踏まえて、絶対値を含んだ不等式を考えてみましょう。$|x|\lt 3$ というのは、原点からの距離が3未満の範囲ということなので、$-3\lt x\lt 3$ であることがわかります。

また、$|x|\gt 3$ の場合は、数直線で考えると「原点からの距離が3より遠い」ということなので、図では次のようになります。$x\lt -3$, $x\gt 3$ が解になることが分かりますね。

まとめると、絶対値を含む不等式には、次のような性質があります。

絶対値を含む不等式

$a\gt 0$ のとき、
　$|x|\lt a$ の解は、$-a\lt x\lt a$
　$|x|\gt a$ の解は、$x\lt -a$, $x\gt a$

続いて、この性質を用いて例題を解いてみます。

例題

次の不等式を解きなさい。
(1) $|x+1|\gt 2$
(2) $|x-2|\leqq 1$

ちなみに、【標準】絶対値を含む一次不等式（場合分け）で取り上げたのと同じ問題です。

(1)は上に書いた性質のうち、2つ目を使います。すると、$x+1\lt -2$, $x+1\gt 2$ が得られます。この2つの不等式を解けば、$x\lt -3$, $x\gt 1$ が解であることがわかります。

(2)は上に書いた性質のうち、1つ目を使います。イコールが入っている点が違いますが、次のようになります。\[ -1\leqq x-2\leqq 1 \]辺々に2を足せば、\[ 1\leqq x\leqq 3 \]が得られます。これが解です。

どちらも、【標準】絶対値を含む一次不等式（場合分け）と同じ問題なので、同じ解になっています。

どっちで解けばいいの？

さて、絶対値を含んだ一次不等式の解き方を見てきました。【標準】絶対値を含む一次不等式（場合分け）とこの記事とで、2種類の解き方を紹介しました。

計算量でいくと、この記事で紹介した解法の方が楽なようにも思います。ただ、1つ注意点としては、この記事で紹介したとき方は、いつでも使えるわけではないということです。

例えば、$|x|+|x+1|\lt 3$ などという問題では、この記事で紹介した方法は使えません。この記事で紹介した方法は、$|x|\gt a$ や $|x|\lt a$ の形になっていないと適用できません。複数の絶対値があったり、右辺にも文字がある場合は、絶対値の中が0以上か負かで場合分けをする方法で、地道に解くしかありません。

なので、絶対値を含む不等式を解くときの解法は