【標準】二次関数y=ax^2+bx+cのグラフ(具体例)
ここでは、今まで見てきた二次関数のグラフの内容を利用して、二次関数 $y=ax^2+bx+c$ のグラフをどうかけばいいのかを見ていきます。
考え方
今まで、次のような二次関数のグラフを見てきました。
- $y=ax^2$ (【基本】二次関数y=ax^2のグラフ)
- $y=ax^2+q$ (【基本】二次関数y=ax^2+qのグラフ)
- $y=a(x-p)^2$ (【基本】二次関数y=a(x-p)^2のグラフ)
- $y=a(x-p)^2+q$ (【基本】二次関数y=a(x-p)^2+qのグラフ)
これらを踏まえて、二次関数 $y=ax^2+bx+c$ のグラフを考えてみましょう。
$y=ax^2+bx+c$ のグラフは、 $ax^2$ と $+c$ の部分だけなら簡単です。 $y=ax^2$ のグラフを上に c だけ動かせば完成です。問題は $+bx$ です。これをどうにかしないといけません。
そこで、【基本】二次関数y=a(x-p)^2+qのグラフで出た例をもう一度ここで見てみます。リンク先の記事では $y=2x^2$ のグラフを、x軸方向に $2$ 、y軸方向に $1$ だけ動かしたグラフを考えていました。これは、 $y=2(x-2)^2+1$ のグラフになるんでしたね。これを展開すると次のようになります。
\begin{eqnarray}
y
&=&
2(x-2)^2+1 \\
&=&
2(x^2-4x+4)+1 \\
&=&
2x^2-8x+9 \\
\end{eqnarray}つまり、 $y=2x^2-8x+9$ のグラフになるということです。これは $y=ax^2+bx+c$ の形になっていますね。このことから何がわかるかというと、この計算を逆に行えば $y=ax^2+bx+c$ は $y=a(x-p)^2+q$ の形に変形できる、ということです。こうなれば頂点の座標がわかるので、グラフもかくことができます。
具体的な例で計算してみましょう。
例
$y=-2x^2-4x+3$
このグラフをかくには、頂点の座標を知る必要があるので、 $y=a(x-p)^2+q$ の形に変形します。このように変形することを平方完成する(complete the square)、といいます。上で行った式変形を逆にたどりつつ考えていきます。
まずは、 $x^2$ の係数でくくります。先ほども書いた通り $+bx$ の部分(今の場合は $-4x$ )が邪魔で、これを消すことが目標なので、定数項はくくりません。
\begin{eqnarray}
y
&=&
-2x^2-4x+3 \\
&=&
-2(x^2+2x)+3
\end{eqnarray}
次に $(x-p)^2$ の部分を作ることを考えましょう。これを展開すると $x^2-2px+p^2$ となります。 x の部分が等しくなるように変形するには $p=-1$ とすればいいですね。これを踏まえて次のように変形します。
\begin{eqnarray}
y
&=&
-2(x^2+2x)+3 \\
&=&
-2\{(x^2+2x+1)-1\}+3 \\
&=&
-2\{(x+1)^2-1\}+3 \\
\end{eqnarray}2行目は $(x+1)^2$ を作り出すための変形をしています。この結果、見かけ上、 $bx$ の部分が消えました。これをさらに計算していくと、次のようになります。
\begin{eqnarray}
y
&=&
-2\{(x+1)^2-1\}+3 \\
&=&
-2(x+1)^2 +2+3 \\
&=&
-2(x+1)^2 +5 \\
\end{eqnarray}これで完成です。この変形によって、このグラフは頂点の座標が $(-1,5)$ で $y=-2x^2$ を平行移動したものであることがわかります。グラフは次のようになります。
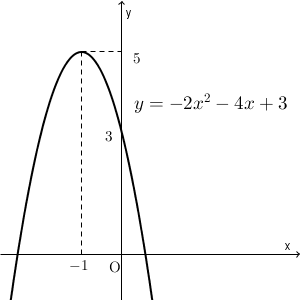
$y=-2x^2-4x+3$ のままだとどういうグラフかはわかりにくいですが、 $y=-2(x+1)^2+5$ と変形できれば、頂点の座標もわかり、グラフがかけるようになります。
グラフをかくためには頂点を知る必要があり、そのためには上のような式変形(=平方完成)を行わないといけない、ということです。はじめのうちは、なかなかむずかしく感じると思います。
おわりに
ここでは、二次関数 $y=ax^2+bx+c$ のグラフのかき方を見てきました。グラフをかくためには、頂点を求めるための式変形が必要でした。次はこの式変形だけを抜き出して、もう一度見ていくことにします。【標準】平方完成のやり方に進みましょう。





